Produit scalaire dans le plan : corrigé des exercices de maths en 1ère en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – résoudre une équation avec des cosinus.
1) Changement de variable.
On pose 
![x \in [-1 ; 1]](https://maths-pdf.fr/latex-images/6027d49c783ce5adf97f75f304b0f52d.png)
a) Équation du second degré équivalente à (1) :
L’équation initiale est :
En posant 
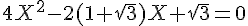
b) Calcul du discriminant :
Le discriminant 
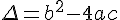
Avec 
![\Delta=[-2(1+\sqrt{3})]^{2}-4\times4\times\sqrt{3}](https://maths-pdf.fr/latex-images/c730185649c0bdebb8d10bfe121ca89e.png)
Ce qui donne :
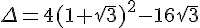
On développe 
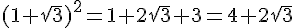
Donc, 
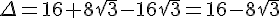
Il semble qu’il y a une erreur dans l’instruction du discriminant donné. Calculons à nouveau, on devait arriver à :
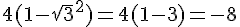
c) Solutions de l’équation du second degré :
Étant donné 
2) Solutions de l’équation (1) dans ![[-\pi ; \pi\]](https://maths-pdf.fr/latex-images/890d75273e6620359f16ec6d1c391f9e.png)

Comme l’équation n’a pas de solutions réelles pour 

Exercice 2 – droite et vecteur normal.
Pour vérifier si la droite d’équation 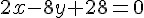
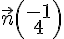
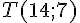
Le vecteur normal de la droite 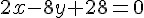
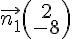
Pour que la droite soit celle de vecteur normal 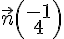
Les vecteurs 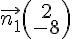
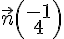
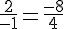
Ceci donne : 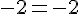
Donc, les vecteurs sont colinéaires, et la droite 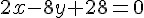
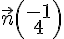
Vérifions maintenant que le point 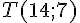
En remplaçant 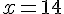
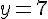
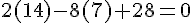
Ce qui donne : 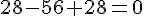
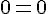
Le point T appartient à la droite.
Conclusion :
Oui, la droite d’équation 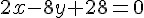
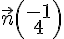
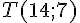
Exercice 3 – rayon et coordonnées du centre du cercle.
1) Cercle 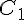
L’équation du cercle est 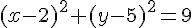
Le centre du cercle est donc (2, 5).
Le rayon est 
2) Cercle 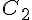
L’équation du cercle est 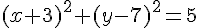
Le centre du cercle est donc (-3, 7).
Le rayon est 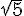
Exercice 4 – droites perpendiculaires.
1) Droites (AB) et (CD) :
Pente de (AB) : 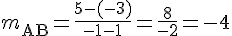
Pente de (CD) : 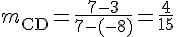
Produit des pentes : 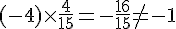
Les droites (AB) et (CD) ne sont pas perpendiculaires.
2) Droite (EF) et 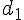
Pente de (EF) : 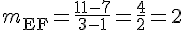
Pente de 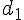
Réécriture : 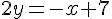
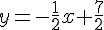
Produit des pentes : 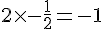
La droite (EF) est perpendiculaire à 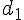
3) Droites 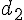
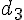
Pente de 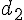
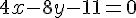
Réécriture : 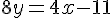
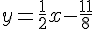
Pente de 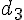
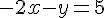
Réécriture : 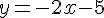
Produit des pentes : 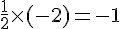
Les droites 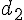
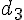
Exercice 5 – exprimer un produit scalaire en fonction de vecteurs.
1) Faire une figure :
Il s’agit de construire un triangle avec les côtés 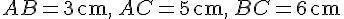
Placez les points A, B, et C avec ces longueurs.
2) Exprimer 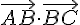
Utilisons la formule du produit scalaire dans un triangle :
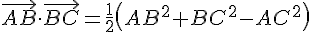
3) En déduire 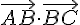
En substituant les valeurs données :
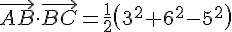
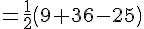
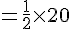
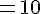
Exercice 6 – calculs de produits scalaires.
1) Calcul du produit scalaire 
Nous appliquons la formule du produit scalaire à l’aide de la relation :
Avec les données : EF = 8, FG = 11, EG = 6, nous avons :
2) Calcul du produit scalaire 
Utilisons la formule des produits scalaires :
3) Calcul du produit scalaire 
En utilisant la formule appropriée :
Exercice 7 – calculer des normes de vecteurs.
1) Calcul des normes :
La norme du vecteur 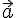
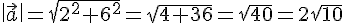
La norme du vecteur 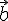
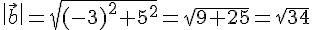
Pour le vecteur 
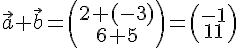
Donc, la norme de 
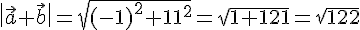
2) Produit scalaire :
Le produit scalaire 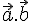
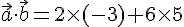
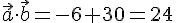
Exercice 8 – calculer des produits scalaires à l’aide de coordonnées.
1) Calcul du produit scalaire de 

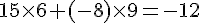
2) Calcul du produit scalaire de 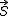
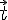
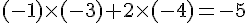
3) Calcul du produit scalaire de 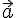
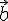
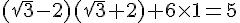
4) Calcul du produit scalaire de 

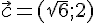
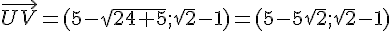
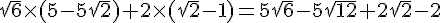
5) Calcul du produit scalaire de 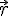
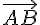
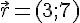
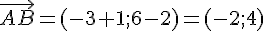
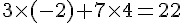
6) Calcul du produit scalaire de 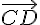
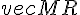
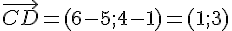
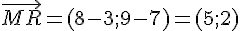
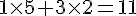
7) Calcul du produit scalaire de 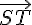
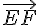
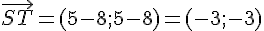
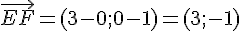
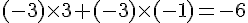
Exercice 9 – déterminer les produits scalaires suivants.
1) 

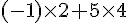
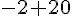
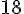
2) 
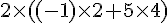
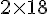
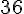
3)
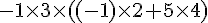
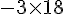
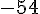
Exercice 10 – ecrire un algorithme qui donne le produit scalaire.
Voici un algorithme simple pour calculer le produit scalaire de deux vecteurs dans un repère orthonormé :
1. Demander à l’utilisateur de saisir les coordonnées du premier vecteur,
2. Demander à l’utilisateur de saisir les coordonnées du deuxième vecteur,
3. Calculer le produit scalaire à l’aide de la formule :
4. Afficher le résultat.
Télécharger ou imprimer cette fiche «produit scalaire dans le plan : corrigé des exercices de maths en 1ère en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.















