Vecteurs et droites du plan : corrigé des exercices de maths en 1ère en PDF

Mis à jour le 25 novembre 2025

Les vecteurs et droites du plan sont des concepts fondamentaux en mathématiques pour les élèves de première. Maîtriser ces notions permet de développer des compétences essentielles telles que l’analyse géométrique et la représentation graphique. Ce sujet joue un rôle clé dans la compréhension des systèmes de coordonnées et des transformations, préparant ainsi les élèves à des études mathématiques plus avancées. Découvrez dans cet article des corrections d’exercices pour renforcer votre apprentissage et optimiser votre réussite.

Exercice 1 – déterminer si les droites sont parallèles.

1) Calculons le coefficient directeur de la droite (AB) :

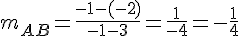
$m_{AB}=\frac{-1-(-2)}{-1-3}=\frac{1}{-4}=-\frac{1}{4}$

Calculons le coefficient directeur de la droite (CD) :

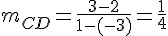
$m_{CD}=\frac{3-2}{1-(-3)}=\frac{1}{4}$

Les droites (AB) et (CD) ne sont pas parallèles.

2) Coefficient directeur de (AB) :

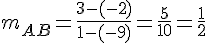
$m_{AB}=\frac{3-(-2)}{1-(-9)}=\frac{5}{10}=\frac{1}{2}$

Coefficient directeur de (CD) :

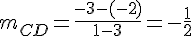
$m_{CD}=\frac{-3-(-2)}{1-3}=-\frac{1}{2}$

Les droites (AB) et (CD) ne sont pas parallèles.

3) Coefficient directeur de (AB) :

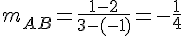
$m_{AB}=\frac{1-2}{3-(-1)}=-\frac{1}{4}$

Coefficient directeur de (CD) :

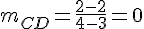
$m_{CD}=\frac{2-2}{4-3}=0$

Les droites (AB) et (CD) ne sont pas parallèles.

4) Coefficient directeur de (AB) :

$m_{AB}=\frac{3-\frac{7}{3}}{\frac{3}{2}-(-\frac{1}{2})}=\frac{2}{2}=\frac{1}{1} = 1$

Coefficient directeur de (CD) :

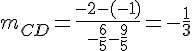
$m_{CD}=\frac{-2-(-1)}{-\frac{6}{5}-\frac{9}{5}}=-\frac{1}{3}$

Les droites (AB) et (CD) ne sont pas parallèles.

5) Coefficient directeur de (AB) :

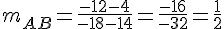
$m_{AB}=\frac{-12-4}{-18-14}=\frac{-16}{-32}=\frac{1}{2}$

Coefficient directeur de (CD) :

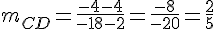
$m_{CD}=\frac{-4-4}{-18-2}=\frac{-8}{-20}=\frac{2}{5}$

Les droites (AB) et (CD) ne sont pas parallèles.

Exercice 2 – montrer que des droites sont parallèles.

1) Points E(2 ; 6) et H(10 ; 6) ont la même ordonnée, donc EH est horizontal.

Calculons la pente de CD :

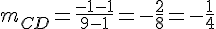
$m_{CD}=\frac{-1-1}{9-1}=-\frac{2}{8}=-\frac{1}{4}$

Les droites CD et EH ne sont pas parallèles car leur pente n’est pas la même.

2) Calculons la pente de EH :

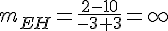
$m_{EH}=\frac{2-10}{-3+3}=\infty$

La droite est verticale. Calculons la pente de CD :

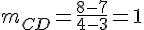
$m_{CD}=\frac{8-7}{4-3}=1$

Les droites CD et EH ne sont pas parallèles.

3) Calculons les pentes :

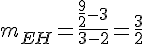
$m_{EH}=\frac{\frac{9}{2}-3}{3-2}=\frac{3}{2}$

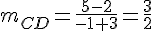
$m_{CD}=\frac{5-2}{-1+3}=\frac{3}{2}$

Les droites CD et EH sont parallèles car leurs pentes sont égales.

4) Calculons les pentes :

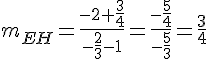
$m_{EH}=\frac{-2+\frac{3}{4}}{-\frac{2}{3}-1}=\frac{-\frac{5}{4}}{-\frac{5}{3}}=\frac{3}{4}$

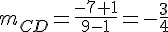
$m_{CD}=\frac{-7+1}{9-1}=-\frac{3}{4}$

Les droites CD et EH ne sont pas parallèles.

5) Calculons les pentes :

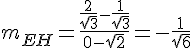
$m_{EH}=\frac{\frac{2}{\sqrt{3}}-\frac{1}{\sqrt{3}}}{0-\sqrt{2}}=-\frac{1}{\sqrt{6}}$

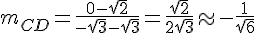
$m_{CD}=\frac{0-\sqrt{2}}{-\sqrt{3}-\sqrt{3}}=\frac{\sqrt{2}}{2\sqrt{3}}\approx-\frac{1}{\sqrt{6}}$

Les droites CD et EH sont parallèles car leurs pentes sont égales.

Exercice 3 – déterminer si des points sont alignés.

1) Les points A(-9 ; 4), B(1 ; -1), et C(4 ; -2).

Pour vérifier l’alignement, calculons le déterminant :

$D=|\begin{array}{ccc} -9 \, 4 \, 1 \\ 1 \, -1 \, 1 \\ 4 \, -2 \, 1 \end{array}|$

Calculons :

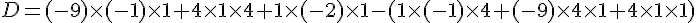
$D=(-9)\times(-1)\times1+4\times1\times4+1\times(-2)\times1-(1\times(-1)\times4+(-9)\times4\times1+4\times1\times1)$

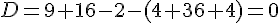
Les points sont alignés.

2) Les points A(-4 ; 0), B(-2 ; 1), et $C(3 ; \frac{7}{2})$ .

Pour vérifier l’alignement, calculons le déterminant :

$D=|\begin{array}{ccc} -4 \, 0 \, 1 \\ -2 \, 1 \, 1 \\ 3 \, \frac{7}{2} \, 1 \end{array}|$

Calculons :

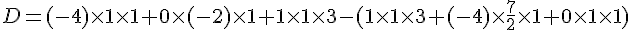
$D=(-4)\times1\times1+0\times(-2)\times1+1\times1\times3-(1\times1\times3+(-4)\times\frac{7}{2}\times1+0\times1\times1)$

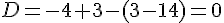
Les points sont alignés.

3) Les points A(-4 ; 4), B(-4 ; 6) , et C(-3 ; 2).

Pour vérifier l’alignement, calculons le déterminant :

$D=|\begin{array}{ccc} -4 \, 4 \, 1 \\ -4 \, 6 \, 1 \\ -3 \, 2 \, 1 \end{array}|$

Calculons :

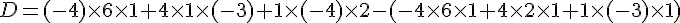
$D=(-4)\times6\times1+4\times1\times(-3)+1\times(-4)\times2-(-4\times6\times1+4\times2\times1+1\times(-3)\times1)$

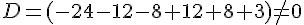
$D=(-24-12-8+12+8+3)\neq0$

Les points ne sont pas alignés.

Exercice 4 – vecteurs colinéaires.

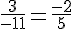
1) Les vecteurs $\vec{u}$ et $\vec{v}$ sont colinéaires si $\frac{3}{-11}=\frac{-2}{5}$ .

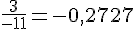
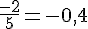
Calculons : $\frac{3}{-11}=-0,2727$ et $\frac{-2}{5}=-0,4$ .

Ces deux valeurs ne sont pas égales, donc ils ne sont pas colinéaires.

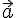
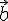
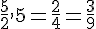
2) Les vecteurs $\vec{a}$ et $\vec{b}$ sont colinéaires si $\frac{5}{2},5=\frac{2}{4}=\frac{3}{9}$ .

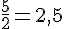
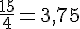
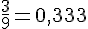
Calculons : $\frac{5}{2}=2,5$ , $\frac{15}{4}=3,75$ , et $\frac{3}{9}=0,333$ .

Ces valeurs ne sont pas égales, donc ils ne sont pas colinéaires.

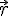
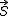
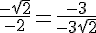
3) Les vecteurs $\vec{r}$ et $\vec{s}$ sont colinéaires si $\frac{-\sqrt{2}}{-2}=\frac{-3}{-3\sqrt{2}}$ .

Simplifions : 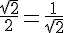$\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}$ .

Ces valeurs sont égales, donc ils sont colinéaires.

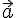
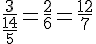
4) Les vecteurs $\vec{a}$ et $\vec{u}$ sont colinéaires si $\frac{3}{\frac{14}{5}}=\frac{2}{6}=\frac{12}{7}$ .

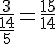
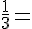
Calculons : $\frac{3}{\frac{14}{5}}=\frac{15}{14}$ et $\frac{1}{3}=$ 0.333.

Ces valeurs ne sont pas égales, donc ils ne sont pas colinéaires.

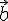
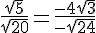
5) Les vecteurs $\vec{b}$ et $\vec{v}$ sont colinéaires si $\frac{\sqrt{5}}{\sqrt{20}}=\frac{-4\sqrt{3}}{-\sqrt{24}}$ .

Simplifions : 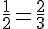$\frac{1}{2}=\frac{2}{3}$ .

Ces valeurs ne sont pas égales, donc ils ne sont pas colinéaires.

Exercice 5 – vérifier si des points sont alignés.

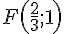
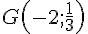
1) Point F : $F\left(\frac{2}{3};1\right)$ , Point G : $G\left(-2;\frac{1}{3}\right)$ , Point H : H(5;2) .

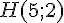
Calcul du déterminant :

$D=|\begin{array}{ccc} \frac{2}{3}\,1\,1\\ -2\,\frac{1}{3}\,1\\ 5\,2\,1\end{array}|$

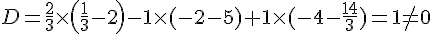
$D=\frac{2}{3}\times\left(\frac{1}{3}-2\right)-1\times(-2-5)+1\times(-4-\frac{14}{3})=1\neq0$

Les points ne sont pas alignés.

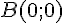
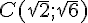
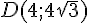
2) Point B : B(0;0) , Point C : $C(\sqrt{2};\sqrt{6})$ , Point D : $D(4;4\sqrt{3})$ .

Calcul du déterminant :

$D=|\begin{array}{ccc} 0\,0\,1\\ \sqrt{2}\,\sqrt{6}\,1\\ 4\,4\sqrt{3}\,1\end{array}|$

D=0

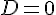
Les points sont alignés.

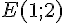
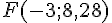
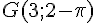
3) Point E : E(1;2) , Point F : , Point G : $G(3;2-\pi)$ .

Calcul du déterminant :

$D=|\begin{array}{ccc} 1\,2\,1\\ -3\,8,28\,1\\ 3\,2-\pi\,1\end{array}|$

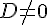
$D\neq0$

Les points ne sont pas alignés.

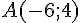
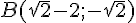
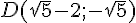
4) Point A : A(-6;4) , Point B : $B(\sqrt{2}-2;-\sqrt{2})$ , Point D : $D(\sqrt{5}-2;-\sqrt{5})$ .

Calcul du déterminant :

$D=|\begin{array}{ccc} -6\,4\,1\\ \sqrt{2}-2\,-\sqrt{2}\,1\\ \sqrt{5}-2\,-\sqrt{5}\,1\end{array}|$

D=0

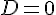
Les points sont alignés.

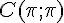
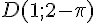
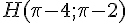
5) Point C : $C(\pi;\pi)$ , Point D : $D(1;2-\pi)$ , Point H : $H(\pi-4;\pi-2)$ .

Calcul du déterminant :

$D=|\begin{array}{ccc} \pi\,\pi\,1\\ 1\,2-\pi\,1\\ \pi-4\,\pi-2\,1\end{array}|$

D=0

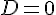
Les points sont alignés.

Exercice 6 – vecteurs colinéaires et parallélogramme.

1) Vecteurs $\vec{u}$ et $\vec{v}$ :

Deux vecteurs sont colinéaires s’il existe un réel k tel que $\vec{v} = k . \vec{u}$ .

Ici, $\vec{u} =(0 ; 1)$ et $\vec{v} = ( -3 ; 0 )$ .
Il n’existe pas de réel k pour que $-3 = k \times 0$ et $0 = k \times 1$ .

Donc, ils ne sont pas colinéaires.

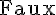
$\text{Faux}$

2) Parallélogramme ABCD :

Dans un quadrilatère ABCD, si $\vec{AB} = 2\vec{CD}$ , cela ne suffit pas à garantir que ABCD est un parallélogramme.

Pour que ce soit un parallélogramme, il faudrait que $\vec{AB} = \vec{CD}$ ou $\vec{AB} + \vec{CD} = \vec{0}$ .

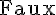
$\text{Faux}$

3) Point E sur [FG] :

Si $\vec{EF} = \frac{5}{6} \vec{FG}$ , alors E est un point de [FG].

Cela signifie que E divise [FG] dans le rapport 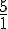$\frac{5}{1}$ , ce qui est possible dans le segment.

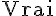
$\text{Vrai}$

4) Vecteurs pour tout x : Pour tout réel x, les vecteurs $\vec{u} = ( \sqrt{2} ; x )$ et $\vec{v} =( \sqrt{18}; 3x)$ sont colinéaires.

Il existe un réel $k = \frac{\sqrt{18}}{\sqrt{2}} = \sqrt{9} = 3$ tel que $\vec{v} = k . \vec{u}$ , donc ils sont colinéaires.

$\text{Vrai}$

Exercice 7 – déterminer les valeurs de x pour que les vecteurs soient colinéaires.

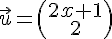
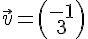
1) Les vecteurs $\vec{u}=\left(\begin{array}{c}2x+1\2\end{array}\right)$ et $\vec{v}=\left(\begin{array}{c}-1\3\end{array}\right)$

sont colinéaires si $\frac{2x+1}{-1} = \frac{2}{3}$ .

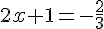
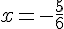
En résolvant : $2x+1=-\frac{2}{3}$ , soit $x=-\frac{5}{6}$

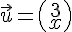
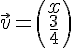
2) Les vecteurs $\vec{u}=\left(\begin{array}{c}3\x\end{array}\right)$ et $\vec{v}=\left(\begin{array}{c}x\\frac{3}{4}\end{array}\right)$

sont colinéaires si $\frac{3}{x} = \frac{x}{\frac{3}{4}}$ .

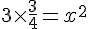
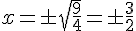
En résolvant : $3\times\frac{3}{4}=x^2$ , soit $x=\pm\sqrt{\frac{9}{4}}=\pm\frac{3}{2}$

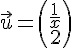
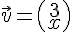
3) Les vecteurs $\vec{u}=\left(\begin{array}{c}\frac{1}{x}\2\end{array}\right)$ et $\vec{v}=\left(\begin{array}{c}3\x\end{array}\right)$

sont colinéaires si $\frac{\frac{1}{x}}{3} = \frac{2}{x}$ .

En résolvant : x=3

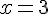
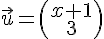
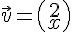
4) Les vecteurs $\vec{u}=\left(\begin{array}{c}x+1\3\end{array}\right)$ et $\vec{v}=\left(\begin{array}{c}2\x\end{array}\right)$

sont colinéaires si $\frac{x+1}{2} = \frac{3}{x}$ .

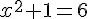
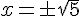
En résolvant : x^2+1=6 , soit $x=\pm\sqrt{5}$

Exercice 8 – déterminer les coordonnées des points d’intersection.

La droite (AB) passant par les points A(7;-1) et B(-7;4)a pour équation :

y=ax+b

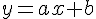
Calculons le coefficient directeur a :

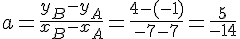
$a=\frac{y_B-y_A}{x_B-x_A}=\frac{4-(-1)}{-7-7}=\frac{5}{-14}$

Donc, 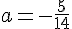$a=-\frac{5}{14}$ .

Utilisons un des points pour trouver b.

Prenons 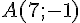A(7;-1) :

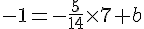
$-1=-\frac{5}{14}\times7+b$

En simplifiant :

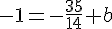
$-1=-\frac{35}{14}+b$

$\Rightarrow b=-1+\frac{35}{14}=\frac{21}{14}$

$\Rightarrow b=\frac{7}{2}$

L’équation de la droite est alors :

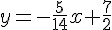
$y=-\frac{5}{14}x+\frac{7}{2}$

Points d’intersection avec les axes :

Axe des ordonnées (x=0) :

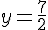
$y=\frac{7}{2}$

Le point d’intersection est $(0\,;\,\frac{7}{2})$ .

Axe des abscisses (y=0) :

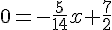
$0=-\frac{5}{14}x+\frac{7}{2}$

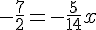
$-\frac{7}{2}=-\frac{5}{14}x$

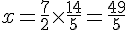
$x=\frac{7}{2}\times\frac{14}{5}=\frac{49}{5}$

Le point d’intersection est 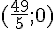$(\frac{49}{5};0)$ .

Exercice 9 – montrer que les vecteurs sont colinéaires avec la relation de Chasles.

Réponse 1 :

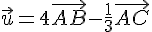
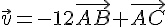
Les vecteurs $\vec{u}=4\vec{AB}-\frac{1}{3}\vec{AC}$ et $\vec{v}=-12\vec{AB}+\vec{AC}$ .

On cherche un réel k tel que $\vec{u} = k \vec{v}$ .

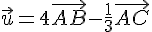
$\vec{u}=4\vec{AB}-\frac{1}{3}\vec{AC}$

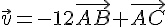
$\vec{v}=-12\vec{AB}+\vec{AC}$

Pour être colinéaires :

$\frac{4}{-12} = \frac{-1}{3} \Rightarrow k = -\frac{1}{3}$ et $-\frac{1}{3} \times 1 = -\frac{1}{3}$ .

Les vecteurs sont colinéaires avec $k = -\frac{1}{3}$ .

Réponse 2 :

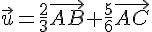
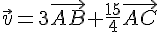
Les vecteurs $\vec{u}=\frac{2}{3}\vec{AB}+\frac{5}{6}\vec{AC}$ et $\vec{v}=3\vec{AB}+\frac{15}{4}\vec{AC}$ .

On cherche un réel k tel que $\vec{u} = k \vec{v}$ .

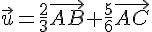
$\vec{u}=\frac{2}{3}\vec{AB}+\frac{5}{6}\vec{AC}$

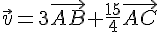
$\vec{v}=3\vec{AB}+\frac{15}{4}\vec{AC}$

Pour être colinéaires :

$\frac{2}{3 \times 3} = \frac{5}{6 \times \frac{15}{4}}$ .

Les vecteurs ne sont pas colinéaires.

Réponse 3 :

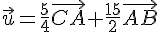
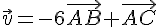
Les vecteurs $\vec{u}=\frac{5}{4}\vec{CA}+\frac{15}{2}\vec{AB}$ et $\vec{v}=-6\vec{AB}+\vec{AC}$ .

On cherche un réel k tel que $\vec{u} = k \vec{v}$ .

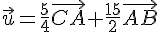
$\vec{u}=\frac{5}{4}\vec{CA}+\frac{15}{2}\vec{AB}$

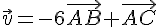
$\vec{v}=-6\vec{AB}+\vec{AC}$

Pour être colinéaires :

$\frac{\frac{15}{2}}{-6} = \frac{\frac{5}{4}}{1}$ .

Les vecteurs sont colinéaires.

Exercice 10 – relation de Chasles et colinéarité.

1) Pour que A soit le milieu de [MB], on doit avoir :

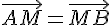
$\vec{AM}=\vec{MB}$

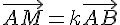
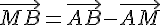
En utilisant la relation donnée $\vec{AM}=k\vec{AB}$ et la relation de Chasles $\vec{MB}=\vec{AB}-\vec{AM}$ :

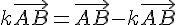
$k\vec{AB}=\vec{AB}-k\vec{AB}$

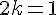
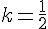
Donc 2k=1 ce qui implique $k=\frac{1}{2}$

2) Pour que M soit sur le cercle de centre B et de rayon 2AB, on a :

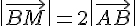
$\|\vec{BM}\|=2\|\vec{AB}\|$

Or, 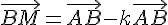$\vec{BM}=\vec{AB}-k\vec{AB}$ donc :

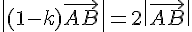
$\|(1-k)\vec{AB}\|=2\|\vec{AB}\|$

Ce qui donne 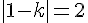|1-k|=2 donc k=-1 ou k=3

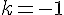
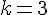
3) Pour que M appartienne à [BA], on doit avoir :

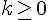
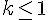
$k\geq0$ et $k\leq1$

Donc $0\leq\, k\leq\,1$

4.9/5 - (31731 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «vecteurs et droites du plan : corrigé des exercices de maths en 1ère en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Second degré et polynômes

Angles orientés et trigonométrie

Limites et variations de suites

Loi binomiale et intervalle de fluctuation

Dérivée

Produit scalaire dans le plan

Les suites

Fonctions usuelles

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 751 885 cours et exercices de maths téléchargés en PDF et 4 250 exercices.