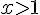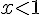Fonction exponentielle : corrigé des exercices de maths en terminale en PDF
Mis à jour le 25 novembre 2025
Dans cet article, nous allons explorer la fonction exponentielle, un concept mathématique essentiel pour les élèves de terminale. Comprendre cette fonction permet de développer des compétences clés en analyse et modélisation, indispensables pour réussir l’épreuve du baccalauréat. Grâce à nos corrections d’exercices, vous renforcerez votre maîtrise des propriétés et applications de la fonction exponentielle, et ainsi, vous serez mieux préparé pour vos futurs défis académiques.
Exercice 1 – position relative de courbes et étude.
Réponse a) :
Pour comparer les fonctions 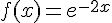
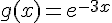
Cela revient à :
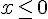
Ainsi, 
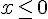
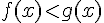

Réponse b) :
Pour comparer les fonctions 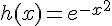
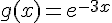
En prenant le logarithme de chaque côté, on obtient :
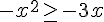
Ce qui se simplifie en :
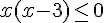
L’étude de signes nous donne :
Donc, 

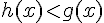
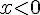

Exercice 2 – fonction et étude de la position relative de la courbe.
La fonction est définie par 
La dérivée de la fonction est : 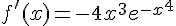
La tangente au point d’abscisse 0 a pour équation :
Calculons f(0) : 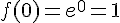
Calculons f'(0) : 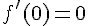
L’équation de la tangente T en 0 est donc : 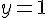
Puisque la dérivée 
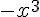

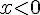

Donc, la courbe 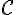
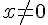
Exercice 3 – aire maximale d’un rectangle et fonctions.
Soit le rectangle OMNP inscrit sous la courbe de la fonction 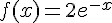
L’aire du rectangle OMNP est donnée par :
Pour maximiser l’aire, nous devons dériver 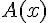
On factorise :
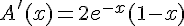
Les solutions de 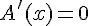
Pour vérifier qu’il s’agit d’un maximum, nous regardons les variations de 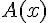
On constate que 

Conclusion : L’aire maximale du rectangle OMNP est atteinte pour 
Les dimensions du rectangle sont :
– Longueur OM =
– Hauteur MP = 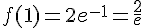
Exercice 4 – la température d’ébullition de l’eau et exponentielle.
1. Température initiale de la casserole : Lorsqu’on plonge la casserole dans l’évier, c’est pour 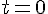
Donc, on a :
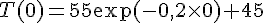
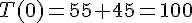
La température initiale est donc 100°C.
2. Vitesse de refroidissement : La vitesse de refroidissement est la dérivée, soit :
![T'(t)=\frac{d}{dt}\left[55\exp(-0,2t)+45\right]](https://maths-pdf.fr/latex-images/07267cf9e470882947c46aab514623fa.png)

a) Proportionnalité :
La vitesse de refroidissement est proportionnelle à l’écart de température entre la casserole et l’eau de l’évier (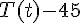
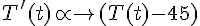
On a alors :
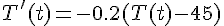
b) Coefficient de proportionnalité :
Le coefficient de proportionnalité est donc -0.2.
3. Température après 5 minutes : Pour 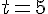
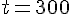
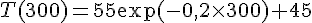
Calculons :
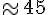
Exercice 5 – simplifier des exponentielles et écrire l’expression.
a)
b)
c)
Pour déterminer le signe de 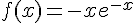
Le signe de 
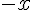
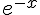
– Si 
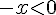
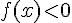
– Si 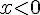
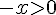
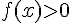
– Si 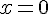
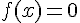
a)
b) 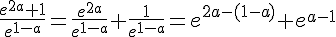
c)
Exercice 6 – relation fonctionnelle et conjecture.
a) Pour conjecturer le signe de 
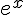
Le signe de 
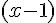
Il en résulte que :
- Pour
- Pour
- Pour
Conjecture : Le signe de 
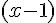
b) Pour démontrer cette conjecture, nous analysons 
Comme 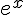
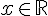

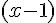
Donc :
- Pour
- Pour
- Pour
La démonstration est alors achevée, vérifiant ainsi notre conjecture initiale.
Exercice 7 – fonction rationnelle avec une exponentielle.
a) Justification que la fonction est définie sur 
La fonction 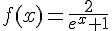
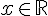
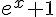

En effet, 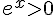

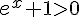
b) Démonstration que 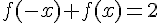
Calculons 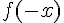
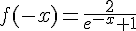
Donc :
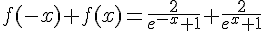
Le dénominateur commun est 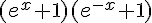
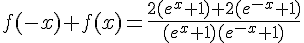
Simplifions le numérateur :
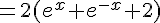
Et le dénominateur, qui est égal à 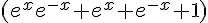
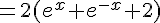
Donc :

c) Conséquence pour la courbe représentative de 
La relation 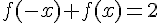

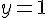
Cela signifie que pour chaque point 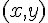
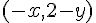
Exercice 8 – vrai ou faux avec les propriétés de l’exponentielle.
a)
Faux. L’égalité est 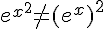
b) Il existe un nombre réel 

Vrai. Pour 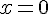
c) Pour tout nombre réel 

Faux. Par exemple, pour 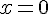
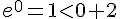
d) Il existe un nombre réel 

Vrai. Pour des valeurs de 
Exercice 9 – axe de symétrie et position relative d’une courbe.
1. Axe de symétrie :
Soit 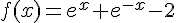
Pour démontrer que l’axe des ordonnées est un axe de symétrie, il faut vérifier que 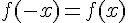
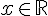
Calculons 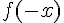
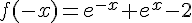
On observe que :
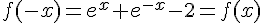
Cela montre que l’axe des ordonnées est un axe de symétrie de 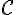
2. a) Expression démontrée :
Nous devons démontrer l’expression suivante :
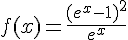
En développant :
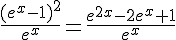
En simplifiant, nous obtenons :
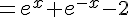
Ceci est bien 
2. b) Position par rapport à l’axe des abscisses :
Vu que 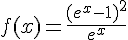
la courbe 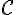
Exercice 10 – le tracé d’une courbe et signe de f(x).
1. a) Déterminer 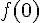
En substituant 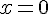
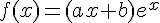
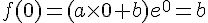
Donc, 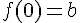
b) Résoudre dans 
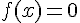
L’équation est 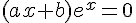
- Pour que
Résolvons 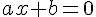
Donc, la solution est 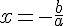
2. a) Sachant que la courbe 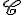
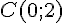
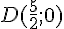


Pour le point 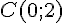
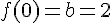
Donc, 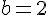
Pour le point 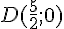
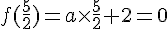
Donc, 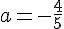
b) Déterminer le signe de 

La fonction est définie par 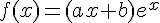
Signe de 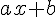
- Pour
- Pour
- Pour
Comme 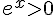


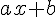
En utilisant les valeurs trouvées 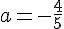
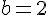
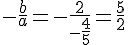
Donc, le signe de 
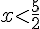

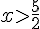
Télécharger ou imprimer cette fiche «fonction exponentielle : corrigé des exercices de maths en terminale en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.