Longueur, masse et volume : corrigé des exercices de maths en CM2 en PDF
Mis à jour le 23 novembre 2025
Exercice 1 – effectuer chaque conversion de longueurs.
a. 58 m en cm :
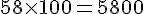
b. 2 567 m en km :
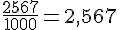
c. 4 hm et 25 m en dm :
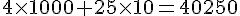
d. 72 dam et 6 cm en hm :
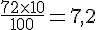
e. 8,049 dam en dm :
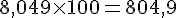
f. 12,8 cm en m :
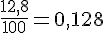
Exercice 2 – convertir chaque mesure en mètres.
Exercice 3 – compléter chaque conversion.
a. Le pont de Normandie a pour longueur 2 141 m, soit 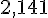
b. Le Boeing 747 a pour hauteur 1 930 cm, soit 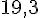
c. Un œuf d’abeille a pour longueur environ 0,015 dm, soit 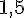
d. Une maquette de 2 CV Citroën a pour largeur 62 mm, soit 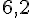
Exercice 4 – problème de la tortue.
La tortue d’Hermann marche en moyenne 80 m par jour. Nous devons d’abord convertir cette distance en kilomètres :
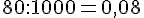
La tortue hiberne de début novembre à fin mars, ce qui représente 5 mois ou environ 150 jours. Ainsi, elle est active pendant :
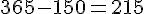
La distance totale parcourue en une année est donc :
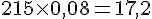
La tortue d’Hermann parcourt donc en moyenne 17,2 km par an.
Exercice 5 – problème du billet.
Calcul :
Chaque billet a une épaisseur de 0,12 mm, soit 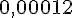
Avec 20 000 billets, la hauteur en mètres est :
La hauteur de la pile de 20 000 billets est de 2,4 mètres.
Exercice 6 – capacités de récipients.
a. Le récipient de 5 L est rempli à moitié : 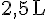
b. Le récipient de 100 L est rempli à un quart : 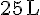
c. Le récipient de 1 daL (10 L) est rempli à trois-quarts : 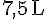
d. Le récipient de 750 mL est rempli aux deux tiers : 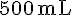
Exercice 7 – la capacité de récipients d’eau.
Récipient a : La capacité est de 1 L et il contient 0,7 L d’eau, il est donc rempli à
Récipient b : La capacité est de 100 mL et il contient 85 mL d’eau, il est donc rempli à
Récipient c : La capacité est de 50 L et il contient 0,5 daL (c’est-à-dire 5 L) d’eau, il est donc rempli à
Récipient d : La capacité est de 1 L et il contient 800 mL (c’est-à-dire 0,8 L) d’eau, il est donc rempli à
Exercice 8 – convertir des volumes.
Choisis l’unité la mieux adaptée :
a. Un réservoir de voiture : Litres (L)
b. Un seau : Litres (L)
c. Une seringue : Millilitres (mL)
d. Une citerne d’essence : Kilolitres (kL)
e. Une canette de soda : Millilitres (mL)
f. Une larme : Millilitres (mL)
Convertis chaque mesure dans une unité plus adaptée :
a. 55 000 mL = 55 L
b. 120 000 cL = 1 200 L
c. 0,0015 hL = 0,15 L
d. 0,0332 daL = 0,332 L
e. 4 500 L = 4,5 kL
f. 1 300 000 mL = 1 300 L
Convertis chaque mesure en millilitres :
a. 13 L = 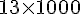
b. 320 daL = 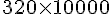
c. 0,00028 hL = 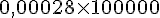
d. 0,19 daL = 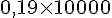
e. 300 L = 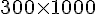
f. 0,03 dL = 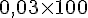
Exercice 9 – une canette de soda et son volume.
Une canette contient initialement 33 cL de soda.
On remplit un verre de 2 dL.
Sachant que 

Il reste donc :
Conclusion : Il reste 13 cL de soda dans la canette.
Exercice 10 – problème de la baignoire.
Étape 1 : Convertissons les hectolitres en litres. 1 hectolitre (hL) = 100 litres (L).
Donc,
Étape 2 : Calculons le nombre de bouteilles de 1,5 L que l’on peut remplir avec 240 L.
Nombre de bouteilles = 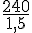
Calculons : 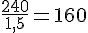
On peut remplir 160 bouteilles de 1,5 L avec le contenu de la baignoire.
Télécharger ou imprimer cette fiche «longueur, masse et volume : corrigé des exercices de maths en CM2 en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.



















