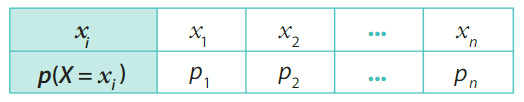Variable aléatoires : cours de maths en 1ère à imprimer en PDF.
Mis à jour le 20 décembre 2025
Les variables aléatoires réelles et les probabilités à travers un cours de maths en 1ère à télécharger en PDF. Dans cette leçon, l’élève devra connaître la définition d’une variable aléatoire, d’un événement et d’un univers. Développer des compétences en calculant l’espérance, la variance et l’écart-type et appliquer les propriétés des indicateurs en première.
I. Calculer des fréquences
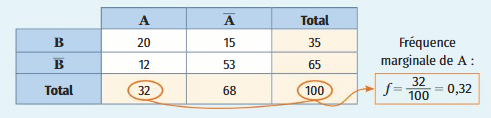
Les sommes des lignes et des colonnes d’un tableau double entrée sont appelées les marges du tableau.
Elles apparaissent en jaune dans le tableau ci-dessous.
La fréquence marginale d’une valeur est le quotient de l’effectif total de cette valeur par l’effectif total.
Remarque :
On parle de fréquence marginale car on utilise uniquement les nombres situés dans la marge du tableau.
Exemple :
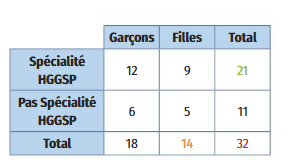
On considère une classe de première constituée de 32 élèves ayant choisi ou non la spécialité HGGSP.
Sur l’ensemble des 32 élèves de la classe, 21 ont choisi la spécialité HGGSP.
La fréquence marginale de la valeur « spécialité HGGSP » est donc 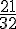
Sur l’ensemble des 32 élèves de la classe, 14 sont des filles.
La fréquence marginale de la valeur « filles » est donc égale à 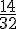
vide B de la série statistique, on dit que l’on calcule la fréquence conditionnelle de la valeur A parmi B.
Cette fréquence conditionnelle, notée
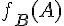
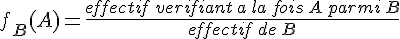
Remarque :
On parle de fréquence conditionnelle car on calcule la fréquence d’une valeur en imposant une condition.
Exemple :
On reprend l’exemple ci-dessus et on cherche connaitre la fréquence de filles (valeur A) parmi les élèves
n’ayant pas choisi la spécialité HGGSP (sous-population B).
Dans le tableau, on lit qu’il y a 5 filles qui n’ont pas choisi la spécialité HGGSP sur un total de 11 élèves qui ne suivent pas cette spécialité.
5
Ainsi, 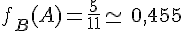
Parmi les élèves qui ne sont pas inscrits en HGGSP, il y a environ 45,5 % de filles.
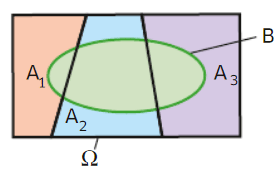
II. Calculer des probabilités
Soit A et B deux événements d’un même univers de probabilité non nulle.
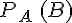
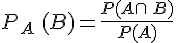
Exemple :
On reprend l’exemple précédent. On choisit un élève de la classe au hasard et on considère les événements :
A : « L’élève a choisi la spécialité HGGSP » et B : « L’élève est un garçon ».
On utilise le tableau pour trouver 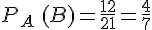
La probabilité de choisir un garçon sachant que l’élève choisi suit la spécialité HGGSP est de 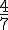
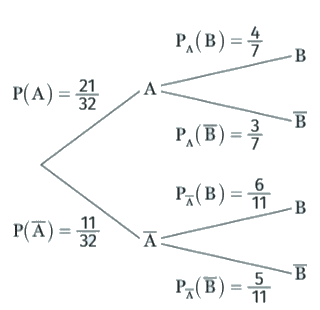
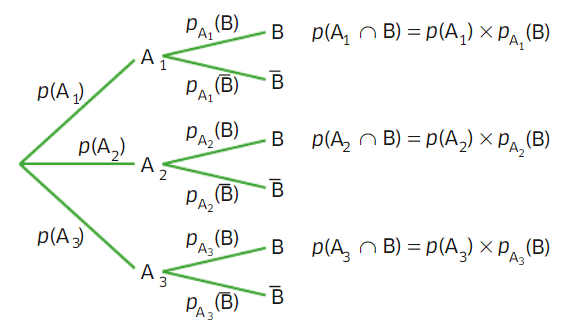
La deuxième série de branche selon le deuxième événement, etc.
On indique sur chaque branche de l’arbre la probabilité correspondante comme indiquée sur l’arbre ci-dessous.
Les probabilités du deuxième niveau de l’arbre sont des probabilités conditionnelles.
égale à 1.
2. On appelle chemin une suite de branches décrivant une succession d’événements. La probabilité d’un
chemin est égale au produit des probabilités situées sur les branches qui le composent.
3.La probabilité d’un événement est la somme des probabilités des chemins qui y aboutissent.
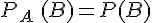
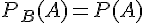
Remarque :
Intuitivement, cela signifie que la probabilité que B se réalise ne dépend pas de la réalisation de l’événement A.
Exemple :
En conservant le même exemple, on observe que 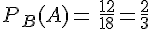
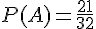
On en déduit que les événements A et B ne sont pas indépendants.
III. Variables aléatoires réelles
On considère une expérience aléatoire dont l’univers 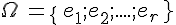
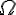
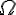
Notation :
a étant un nombre réel, on note 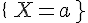
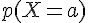
Exemple :

Une urne contient 6 boules indiscernables au toucher : trois boules sont rouges numérotées de 1 à 3 (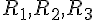
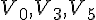
Un joueur mise 2 € et tire une boule au hasard. Si elle est rouge, il gagne 3 ; si elle est verte, il gagne en euros la valeur du numéro indiqué.
L’univers associé à l’expérience aléatoire est 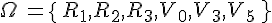
Toutes les issues sont équiprobables.
La variable aléatoire X qui, à chaque boule choisie, associe le gain en tenant compte de la mise, peut
prendre comme valeur : 3 (en prenant la boule 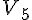
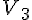
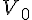
L’événement « X Prend la valeur 3 », noté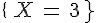
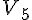
Sa probabilité est 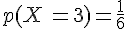
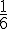
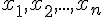
Lorsqu’à chaque valeur
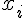
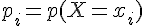
Remarques :
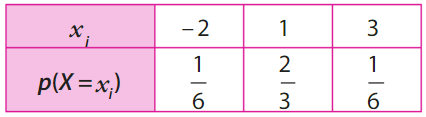
La loi de probabilité d’une variable aléatoire X peut se présenter sous la forme d’un tableau.
• La somme des probabilités de toutes valeurs prises par la variable aléatoire est égale 1.
On a : 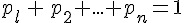
Exemple :
Dans l’exemple précédent, X peut prendre les valeurs 3, 1 et —2. De plus, on a :
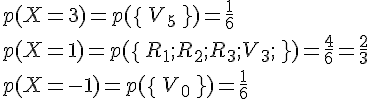
On en déduit que la loi de probabilité de X est donnée dans le tableau ci-dessous.
Remarques :
Les notations 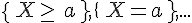
Dans l’exemple, on peut calculer la probabilité de l’événement 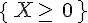
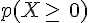
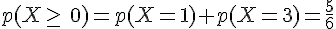
IV. Espérance, variance et écart-type
1.Définitions et vocabulaire
Dans ce paragraphe, X est une variable aléatoire dont la loi de probabilité est donnée par le tableau suivant.
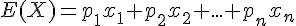
Exemple :
On considère une variable aléatoire Y dont la loi de probabilité est donnée par le tableau suivant.
On a : 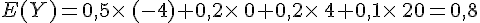
Remarques :
• Lorsque X est une variable aléatoire donnant le gain algébrique à un jeu, E(X) est le gain moyen que peut espérer un joueur sur un grand nombre de parties à ce jeu.
• un jeu est équitable si l’espérance de la variable aléatoire donnant le gain algébrique est nulle.
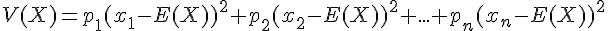
Exemple :
Dans l’exemple précédent, on a :
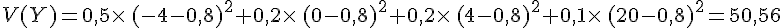
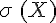
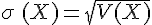
Exemple :
Dans l’exemple précédent, on a : 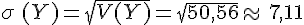
Remarques :
• Ces définitions sont à mettre en lien avec celles de moyenne, variance et écart-type d ‘une série statistique. On peut donc aussi utiliser la calculatrice ou un tableur pour déterminer l’espérance, la variance et l’écart-type d’une variable aléatoire si on a résumé la loi de probabilité de la variable aléatoire dans un tableau.
• Comme en statistiques, l’écart-type permet de se donner une idée de la répartition des valeurs prises par une variable autour de son espérance en tenant compte des probabilités. Plus l’écart-type est grand, plus les valeurs prises par la variable aléatoire sont » éloignées » de l’espérance.
2.Propriétés des indicateurs
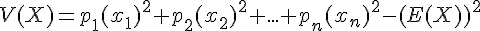
issue donnant la valeur
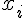
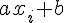
Cette nouvelle variable aléatoire se note aX + b.
Exemple :
Z est une variable aléatoire donnant le gain en euros à un jeu auquel on gagner 2, 4 ou 8 €.
Z Peut donc prendre les valeurs 2, 4 ou 8.
Les organisateurs décident de multiplier les gains par 2 puis de soustraire 1 €.
On obtient alors la variable aléatoire Z’ telle que Z’ = 2Z— 1 , qui donne les gains en euros suite à cette modification.
Z’ peut prendre les valeurs 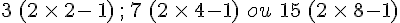
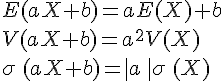
Démonstration :
Pour l’espérance :
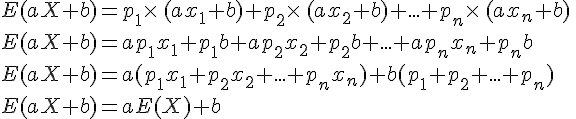
car 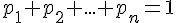
Remarque :
Voir les exercices d’approfondissement pour la propriété de la variance (et donc de
Exemple :
Dans l’exemple précédent, si on a 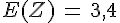
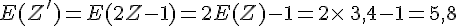
aléatoire (lors de simulations par exemple) la moyenne des valeurs de cet échantillon est proche de la
valeur de l’espérance de cette variable aléatoire.
Remarque :
Le tableur et Python permettent de faire des simulations et d’obtenir au hasard une
valeur prise par une variable aléatoire.
Télécharger ou imprimer cette fiche «variable aléatoires : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Première
Exercices de Première
Nos applications
Téléchargez la dernière version gratuite de nos applications.