Les équations et les inéquations du second degré : cours de maths en 1ère à imprimer en PDF.

Mis à jour le 23 février 2026

Sommaire

Les équations et les inéquations du second degré avec le discriminant dans un cours de maths en 1ère avec les différentes formules pour résoudre l’équation. L’élève devra savoir calculer la valeur du discriminant delta et déterminer la valeur des racines puis, devra être capable de tracer la parabole en première.

I. Fonction polynôme du second degré

1.Généralités

Définition :

Toute fonction f définie sur

par

avec a,b,c trois nombres réels tel que

soit non nul est appelée fonction polynôme du second degré ou, simplement, trinôme.

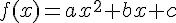
2.Forme canonique

Théorème :

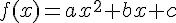
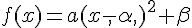
Tout fonction f du second degré définie sur $\mathbb{R}$ par avec a,b,c trois nombres réels tel que soit non nul peut s’écrire de façon unique sous la forme $f(x)=a(x-,\alpha,)^2+\beta$ .Cette forme est appelée la forme canonique du trinôme.

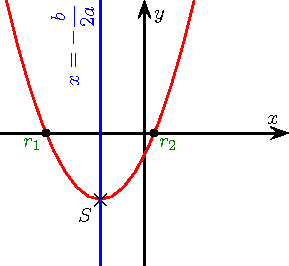
La courbe représentative de f est appelée la parabole et son équation est .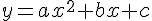

Exemple :

Déterminer la forme canonique de la fonction suivante :

$f(x)=2x^2-4x+8\\f(x)=2(x^2-2x+4)\\f(x)=2[(x-1)^2-1+4]\\f(x)=2[(x-1)^2+3]\\f(x)=2(x-1)^2+6$

Propriété :

Une parabole de sommet

est symétrique par rapport à la droite d’équation

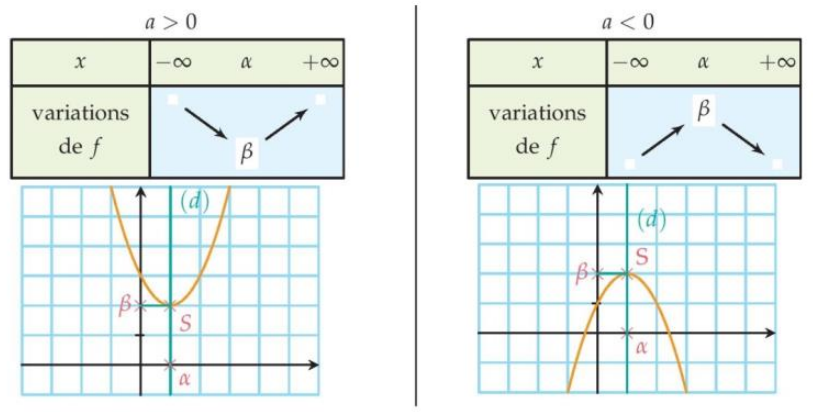
3.Sens de variation d’une fonction

Propriété :

Soit f une fonction du second degré dont la forme canonique est 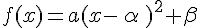$f(x)=a(x-\,\alpha\,)^2+\beta$ .

Le sens de variation de f dépend du signe du nombre a.

Vocabulaire :

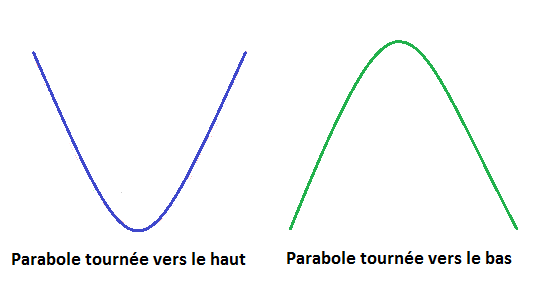
Si a>0, f admet un minimum en x=a égal à b que l’on peut traduire par « le sommet de la parabole est en bas » ou par « f est convexe« .
Si a<0, f admet un maximum en x=a égal à b que l’on peut traduire par « le sommet de la parabole est en haut » ou par « f est concave« .

II. Les équations du second degré et trinôme

1.Résolution d’équations du second degré

Définition : équation du second degré.

Une équation du second degré est une équation du type

avec a,b,c trois nombres réels tel que

soit non nul.

Définition : discriminant.

est le discriminant du trinôme du second degré

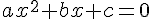
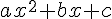
Vocabulaire :

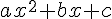
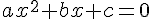
On appelle racine du trinôme du second degré les solutions de l’équation .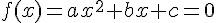

Les solutions de l’équation sont appelées racines ou zéros de la fonction f.

Théorème :

Le nombre de solutions de l’équation du second degré dépend du signe de $\Delta$ .

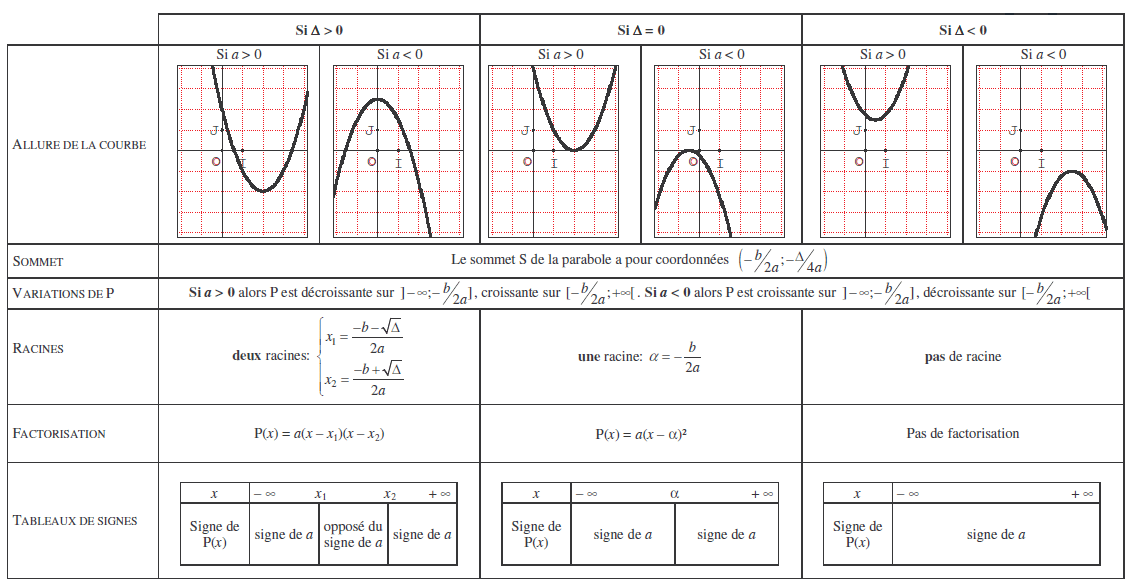
2.Le signe du trinôme

III. Les équations en maths du second degré et les trinômes

P(x) = ax² + bx + c est un trinôme du second degré (a non nul).

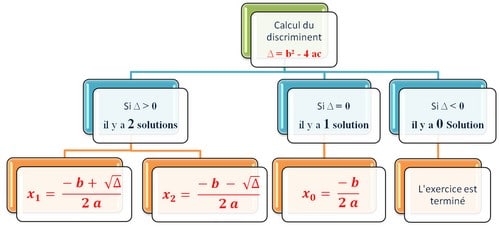
IV. Résolution des équations du second degré

4.9/5 - (30038 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les équations et les inéquations du second degré : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 15 594 257 cours et exercices de maths téléchargés en PDF et 4 250 exercices.