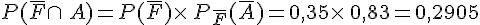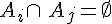Probabilités conditionnelles et indépendance : cours de maths 1ère.

Sommaire

1 I. Probabilité conditionnelle
2 II. Arbres pondérés
- 2.1 1. Arbres pondérés et probabilité conditionnelle
- 2.2 2.Formule des probabilités totales
3 III. Notion d’indépendance
- 3.1 1.Indépendance de deux événements
- 3.2 2.Succession de deux épreuves indépendantes

Les probabilités conditionnelles et la notion d’indépendance à travers un cours de maths en 1ère à télécharger en PDF. Nous aborderons les arbres pondérés et les événements indépendants et nous calculerons différentes probabilités à travers différents exemples issus de la vie courante et similaires à ceux de votre manuel scolaire.

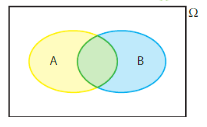
Dans tout le chapitre, A et B désignent deux événements d’un univers 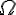$\Omega$ et p une probabilité sur $\Omega$ .

I. Probabilité conditionnelle

Dans ce paragraphe, on considère que 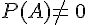$P(A)\neq\,0$ .

Définition :probabilité conditionnelle.

P_A(B) désigne la probabilité que l’événement B soit réalisé sachant que A est réalisé.On dit que c’est une probabilité conditionnelle.

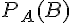
Exemple :

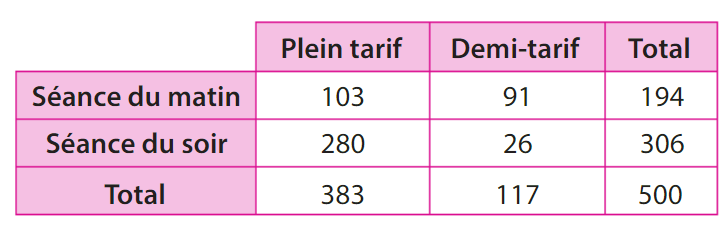
On donne ci-dessus la répartition des spectateurs sur une journée dans une salle
de cinéma selon les séances et le tarif.
On choisit un de ces spectateurs au hasard et on considère les événements :
• M : « La personne a assisté à la séance du matin ».
• D : » La personne a payé demi-tarif ».

La probabilité que la personne ait assisté à la séance du matin sachant qu’elle a payé demi-tarif est

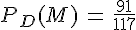
$P_D(M)\,=\,\frac{91}{117}$ car parmi les 117 personnes ayant payé demi-tarif, 91 sont venues le matin.

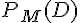
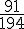
De même, , la probabilité que la personne ait payé demi-tarif, sachant qu’elle a assisté à la séance du matin est $\frac{91}{194}$ .

Propriété : probabilité conditionnelle et intersection

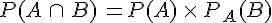
On a, de manière équivalente, $P(A\,\cap\,B)\,=P(A)\,\times \,P_A(B)$

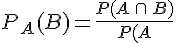
et $P_A(B)=\frac{P(A\,\cap\,B)}{P(A}$ .

Exemple :
On tire un objet au hasard dans le stock d’une usine constitué de claviers (événement C) et de souris
(événement S) en deux versions, familiale (événement F) et gamer (événement G).
30 % du stock est constitué de souris et, de plus, 40 % des souris sont des souris gamer.
Par ailleurs, 63 % du stock est constitué de claviers familiaux.
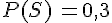
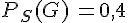
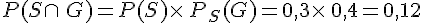
• D’après l’énoncé, $P(S)\,=0,3$ et $P_S(G)\,=0,4$ donc $P(S\cap\,G)=P(S)\times \,P_S(G)=0,3\times \,0,4=0,12$ c’est-à-dire que la
probabilité que l’objet soit une souris gamer est O, 12.
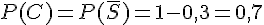
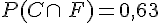
• D’après l’énoncé $P(C)=P(\overline{S})=1-0,3=0,7$ et $P(C\cap\,F)=0,63$ .

La probabilité de tirer un objet familial au hasard sachant que c’est un clavier est donc

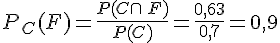
$P_C(F)=\frac{P(C\cap\,F)}{P(C)}=\frac{0,63}{0,7}=0,9$ .

Remarques :

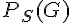
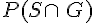
• Attention à ne pas confondre et $P(S\cap\,G)$ : la phrase » 40 % des souris sont des souris gamer » veut bien dire que, si l’on sait que l’objet est une souris, alors, il y a « 40 % de chance » qu’elle soit gamer, ce qui correspond bien à .
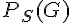
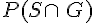
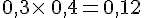
• Le calcul de $P(S\cap\,G)$ revient à utiliser la formule des « proportions de proportions » il y a 30 % de souris dont 40 % gamer donc la proportion de souris gamer est $0,3\times \,0,4=0,12$ soit 12 %.

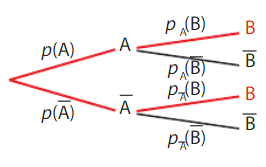
II. Arbres pondérés

1. Arbres pondérés et probabilité conditionnelle

Propriété : arbre pondéré et règle du produit.

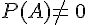
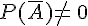
Soit A tel que $P(A)\neq\,0$ et $P(\overline{A})\neq\,0$ .
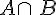
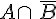
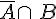
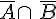
Dans l’arbre pondéré ci-dessous, les probabilités des événements $A\cap\,B$ , $A\cap\,\overline{B}$ , $\overline{A}\cap\,B$ et $\overline{A}\cap\,\overline{B}$ peuvent être obtenues en multipliant entre-elles les probabilités écrites sur les branches qui « mènent » à l’événement.

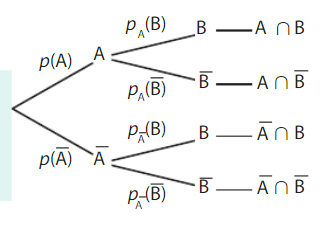
Remarque :
Cette propriété découle de manière immédiate de la propriété 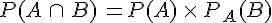$P(A\,\cap\,B)\,=P(A)\,\times \,P_A(B)$ .

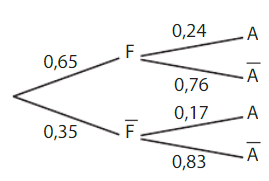
Exemple :
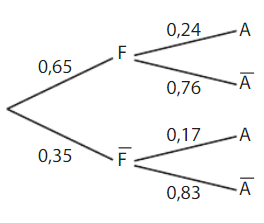
Dans un lycée, les élèves de terminale faisant la spécialité mathématiques, se répartissent ainsi :
• 65 % de filles, dont 24 % souhaitent faire PACES.
• 35 %de garçons, dont 17 % souhaitent faire PACES.
On tire au sort un de ces élèves et on considère les événements F : » L’élève est une fille » et

A : » L’élève souhaite faire PACES ».
On Peut représenter la situation par l’arbre pondéré ci-dessous.
La probabilité que l’élève tiré au sort soit une fille qui souhaite faire PACES est :

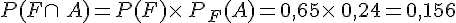
$P(F\cap\,A)=P(F)\times \,P_F(A)=0,65\times \,0,24=0,156$ .
La probabilité que l’élève tiré au sort soit un garçon qui ne souhaite pas faire PACES est :

$P(\overline{F}\cap\,A)=P(\overline{F})\times \,P_{\overline{F}}(\overline{A})=0,35\times \,0,83=0,2905$ .

Définition : partition de l’univers.

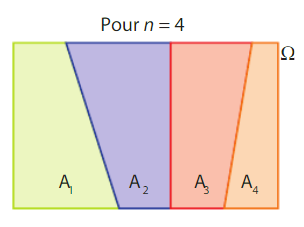
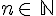
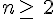
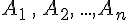
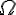
Soit n (avec $n\in\,\mathbb{N}$ et $n\geq\,\,2$ ) événements de probabilités non nulles $A_1\,,\,A_2,\,...,A_n$ .Ces événements forment une partition de l’univers $\Omega$ (ou un système complet d’événements) si :

ils sont disjoints deux deux, c’est-à-dire que $A_i\cap\,A_j=\emptyset$ si $i\neq\,j$ .
$A_1\cup\,A_2\cup\,....\cup\,A_n=\Omega$

Remarque :

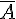
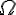
Un événement A et son événement contraire $\overline{A}$ forment une partition de l’univers $\Omega$ .

Propriété : arbre pondéré et partition.

On peut construire des arbres avec plus de deux branches partant d’un même noeud tant que
tous les événements « reliés à un même noeud » forment une partition de l’univers.

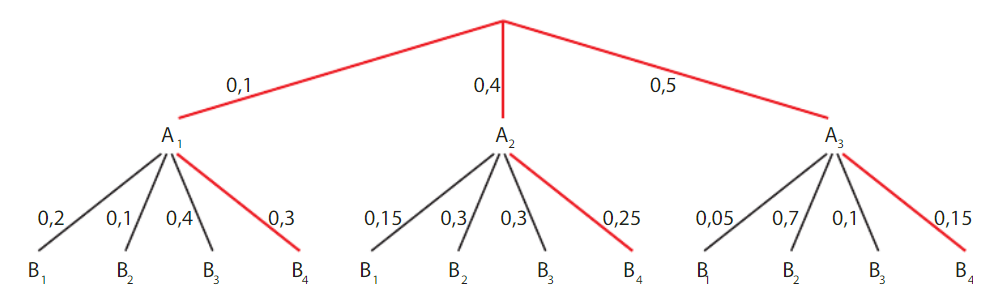
Exemple :
Soit 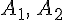$A_1,\,A_2$ et formant une partition de l’univers.
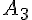
Dans l’arbre ci-dessous, les événements reliés à un même noeud
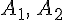
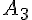
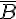
( $A_1,\,A_2$ et d’une part et B et $\overline{B}$ d’autre part) forment des partitions de l’univers, c’est donc bien un arbre pondéré.
On peut y calculer par exemple :
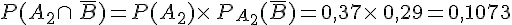
$P(A_2\cap\,\overline{B})=P(A_2)\times \,P_{A_2}(\overline{B})=0,37\times \,0,29=0,1073$

2.Formule des probabilités totales

Propriété : formule des probabilités totales (cas particulier).

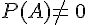
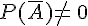
Soit A tel que $P(A)\neq\,0$ et $P(\overline{A})\neq\,0$ ..
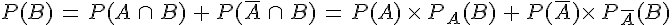
La probabilité de B est donnée par la formule $P(B)\,=\,P(A\,\cap\,B)\,+\,P(\overline{A}\,\cap\,B)\,=\,P(A)\,\times \,P_A(B)\,+\,P(\overline{A})\times \,P_{\overline{A}}(B)$

Démonstration :

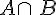
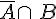
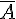
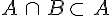
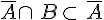
• $A\cap\,B$ (en vert sur le graphique) et $\overline{A}\cap\,B$ (en bleu sur le graphique) sont disjoints puisque A et $\overline{A}$ sont disjoints et que $A\,\cap\,B\subset\,A$ et $\overline{A}\cap\,B\subset\,\overline{A}$ .
• D’autre part, 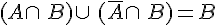$(A\cap\,B)\cup\,(\overline{A}\cap\,B)=B$ .
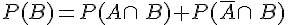
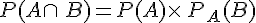
On en déduit que $P(B)=P(A\cap\,B)+P(\overline{A}\cap\,B)$ puis, comme $P(A\cap\,B)=P(A)\times \,P_A(B)$

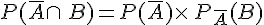
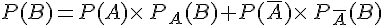
et $P(\overline{A}\cap\,B)=P(\overline{A})\times \,P_{\overline{A}}(B)$ , que $P(B)=P(A)\times \,P_A(B)+P(\overline{A})\times \,P_{\overline{A}}(B)$ .

Remarque :

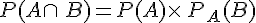
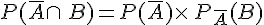
Sur un arbre pondéré, on peut comprendre la formule des probabilités totales comme le fait que l’on additionne les probabilités $P(A\cap\,B)=P(A)\times \,P_A(B)$ et $P(\overline{A}\cap\,B)=P(\overline{A})\times \,P_{\overline{A}}(B)$ associées aux « chemins » pour lesquels B est réalisé, représentés en rouge sur l’arbre ci-dessous.

Exemple :
On reprend l’exemple des élèves d’un lycée faisant la spécialité mathématiques (du paragraphe 2. a du cours) .
La probabilité qu’un élève souhaite faire PACES est :
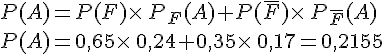
$P(A)=P(F)\times \,P_F(A)+P(\overline{F})\times \,P_{\overline{F}}(A)\,\\P(A)=0,65\times \,0,24+0,35\times \,0,17=0,2155$

Propriété : formule des probabilités totales (cas général).

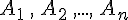
Soit $A_1\,,\,A_2\,,...,\,A_n$ d’une part et

d’autre part formant deux partitions de l’univers.
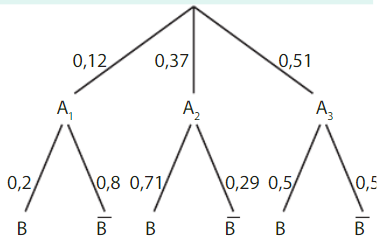
Pour i entier entre 1 et m, la probabilité de

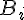
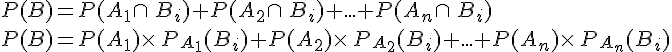
est donnée par la formule : $P(B)=P(A_1\cap\,B_i)+P(A_2\cap\,B_i)+...+P(A_n\cap\,B_i)\,\\P(B)=P(A_1)\times \,P_{A_1}(B_i)+P(A_2)\times \,P_{A_2}(B_i)+...+P(A_n)\times \,P_{A_n}(B_i)$

Exemple :
Pour l’arbre pondéré ci-dessous (on admet que $A_1,\,A_2$ et d’une part et et d’autre part
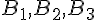
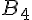
forment deux partitions, on a 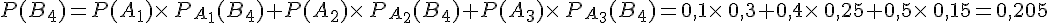$P(B_4)=P(A_1)\times \,P_{A_1}(B_4)+P(A_2)\times \,P_{A_2}(B_4)+P(A_3)\times \,P_{A_3}(B_4)=0,1\times \,0,3+0,4\times \,0,25+0,5\times \,0,15=0,205$

III. Notion d’indépendance

1.Indépendance de deux événements

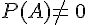
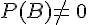
Dans ce paragraphe A et B Sont tels que $P(A)\neq\,0$ et $P(B)\neq\,0$ .

Définition : indépendance de deux événements.

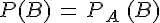
On dit que A et B sont indépendants si $P(B)\,=\,P_A\,(B)$ .

Remarques :
• Concrètement, cela veut dire que le fait que A soit réalisé n’a pas d’influence sur la probabilité de réalisation de B.
• De manière symétrique, on a alors également 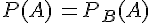$P(A)\,=P_B(A)$ .

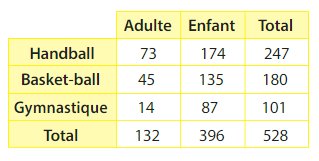
Exemple :
On donne la répartition des licenciés dans un club.
On tire au sort une personne de ce club pour une tombola et on considère

les événements A : « La personne est adulte. » et B : « La personne pratique le basket-ball. »
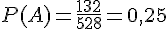
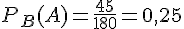
On constate que $P(A)=\frac{132}{528}=0,25$ et $P_B(A)=\frac{45}{180}=0,25$ .

Ainsi, 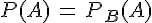$P(A)\,=\,P_B(A)$ donc A et B sont indépendants.

Propriété : indépendance et intersection.

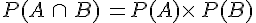
A et B sont indépendants si, et seulement si, $P(A\,\cap\,B)\,=P(A)\times \,P(B)$

Démonstration :
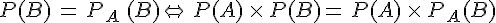
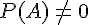
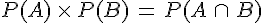
A et B Sont indépendants, si et seulement si, $P(B)\,=\,P_A\,(B)\Leftrightarrow\,P(A)\,\times \,P(B)=\,P(A)\,\times \,P_A(B)$ (car $P(A)\,\neq\,0$ ) c’est-à-dire si et seulement si $P(A)\,\times \,P(B)\,=\,P(A\,\cap\,B)$ .

Exemple :
Dans l’exemple précédent, on appelle G l’événement » La personne pratique la gymnastique ».
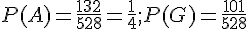
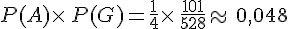
On a alors $P(A)=\frac{132}{528}=\frac{1}{4};P(G)=\frac{101}{528}$ donc $P(A)\times \,P(G)=\frac{1}{4}\times \,\frac{101}{528}\approx\,0,048$ d’une part.

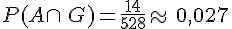
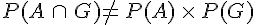
D’autre part, $P(A\cap\,G)=\frac{14}{528}\approx\,0,027$ . Ainsi, $P(A\,\cap\,G)\neq\,P(A)\,\times \,P(G)$ donc A et G ne sont pas indépendants.

Propriété : indépendance et événement contraire.

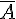
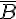
Si A et B sont indépendants, alors $\overline{A}$ et B le sont également, de même que A et $\overline{B}$ et $\overline{A}$ et $\overline{B}$ .

Exemple :
Dans le premier exemple du paragraphe, on a vu que A et B Sont indépendants.
Donc 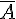$\overline{A}$ : « La personne est un enfant » et B : « La personne pratique le basket-ball » sont indépendants
également.

2.Succession de deux épreuves indépendantes

Définition : succession de deux épreuves indépendantes.

En réalisant successivement deux expériences aléatoires telles que les événements associés à la
première soient indépendants des événements associés à la seconde, on dit que l’on réalise une
succession de deux épreuves indépendantes.

Remarques :
• Deux épreuves sont indépendantes si le résultat de l’une n’a pas d’influence sur le résultat de l’autre.
• L’indépendance fait partie de la modélisation et résulte de l’analyse du modèle physique. Par exemple, quand on réalise une succession de deux tirages avec remise, on considère qu’il y a indépendance car après le premier tirage puis la « remise » on revient » à la situation de départ ».
C’est une modélisation que l’on adoptera systématiquement, mais qui est néanmoins discutable.

Propriété : succession d’épreuves indépendantes et arbre pondéré.

On peut représenter une succession de deux épreuves indépendantes par un arbre dont les
pondérations sont les probabilités (non conditionnelles) des différents résultats pour chacune des
épreuves.

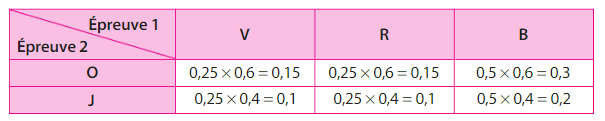
Exemple :
On place 1 boule verte, 1 boule rouge et 2 boules bleues dans une urne 1 et 3 boules oranges et 2 boules
jaunes dans une urne 2.

On tire une boule dans l’urne 1 puis une boule dans l’urne 2.
On admet que ces deux épreuves sont indépendantes, donc que les événements V, R et B : » La 1ère boule est verte, respectivement rouge, respectivement bleue « , sont indépendants des événements O et J :
« la 2ème boule est orange, resp. jaune ».
Ainsi,

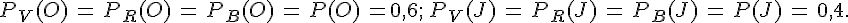
$P_V(O)\,=\,P_R(O)\,=\,P_B(O)\,=\,P(O)\,=0,6;\,P_V(J)\,=\,P_R(J)\,=\,P_B(J)\,=\,P(J)\,=\,0,4.$
On Peut donc représenter la situation par l’arbre ci-dessous.

Remarque :

Les « sous-arbres » correspondant à la deuxième épreuve sont toujours tous identiques.

Propriété : succession d’épreuves indépendantes et tableau à double entrée.

On peut représenter une succession de deux épreuves indépendantes par un tableau double
entrée dont la première ligne contient les résultats de la première épreuve et la première colonne ceux de la seconde épreuve (ou inversement) et les cases intérieures les probabilités associées obtenues par produit.

Exemple :
Dans l’exemple précédent, on aussi représenter la situation par le tableau ci-dessous.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités conditionnelles et indépendance : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Réviser les cours et exercices de maths avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres outils pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Maths PDF c'est 12 687 116 cours et exercices de maths téléchargés en PDF et 4 250 exercices.