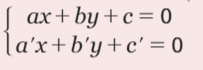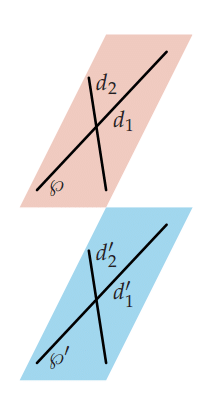Vecteurs, droites et plans : cours de maths en 1ère à imprimer en PDF.

Accueil >> Cours de maths >> Cours en 1ère >> Vecteurs, droites et plans : cours de maths en 1ère à imprimer en PDF.

Mis à jour le 29 mai 2025

📚Cours de MathématiquesPremière • lycée
Vecteurs, droites et plans
⏱️Temps de lecture : 7 min
🎯Difficulté : Avancé
📚Cycle terminal
📋Prérequis : Programme 2nde maîtrisé
📄Format PDF disponible gratuitement
 Les vecteurs, les droites et les plans avec un cours de maths en 1ère. Vous devrez connaître sa définition et savoir calculer des coordonnées et déterminer sa norme dans un repère orthogonal ou orthonormé du plan. L’élève devra pouvoir démontrer si deux vecteurs sont colinéaires ou orthogonaux, puis, déterminer l’équation réduite ou cartésienne d’une droite.

I. Colinéarité de deux vecteurs

Définition :
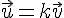
Deux vecteurs non nuls \vec{u} et \vec{v} sont dits colinéaires si, et seulement si, il existe un réel k tel que \vec{u}=k\vec{v}.
Propriété :

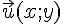
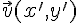
On considère \vec{u}(x;y) et \vec{v}(x',y') deux vecteurs du plan.

Les vecteurs \vec{u} et \vec{v} s sont colinéaires si, et seulement si, leurs coordonnées sont proportionnelles.

Autrement dit, ils sont colinéaires si, et seulement si, xy'-x'y=0.

Propriétés :
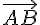
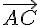
Trois points du plan A,B et C sont alignés si, et seulement si, \vec{AB} et \vec{AC} sont colinéaires.

II.Equation cartésienne d’une droite

Définition:

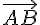
Un vecteur \vec{u} non nul est un vecteur directeur de la droite (AB) si \vec{u} et \vec{AB} sont colinéaires.

Autrement dit, un vecteur non nul est appelé vecteur directeur d’une droite lorsqu’il a la même direction que cette droite.

Propriété :
Deux droites du plan sont parallèles si, et seulement si,  un vecteur directeur de l’une est colinéaire à un vecteur directeur de l’autre.

vecteur directeur droite

Propriété :

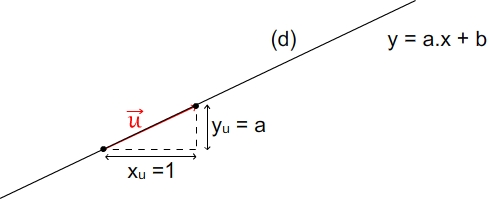
Soient a et b deux nombres réels.

Le vecteur 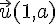\vec{u}(1,a) est un vecteur directeur de la droite d’équation y=ax+b.

vecteur directeur droite équation

Propriété :
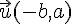
L’ensemble des points M(x;y) du plan tels que ax+by+c=0 avec (a;b)\neq\,(0;0) est une droite de vecteur directeur \vec{u}(-b,a).
Définition :
Une équation d’une droite d de la forme ax+by+c=0 est appelée équation cartésienne de la droite d.

III.Décomposition d’un vecteur

Propriété :

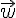
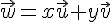
Soient \vec{u} et \vec{v} deux vecteurs du plan non nuls  et non colinéaires .Tout vecteur \vec{w} du plan s’écrit de façon unique sous la forme \vec{w}=x\vec{u}+y\vec{v} où x et y sont deux nombres réels.

Propriété :

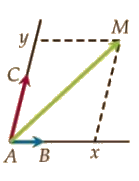
Soient A,B et C trois points non alignés du plan.Pour tout point M du plan, il existe un unique couple de réels (x;y)  tels que \vec{AM}=x\vec{AB}+y\vec{AC}.

Le triplet 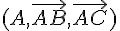(A,\vec{AB},\vec{AC}) définit un repère du plan.

repère plan

IV.Norme d’un vecteur

Définition :

Soient A et B deux points du plan.

La norme du vecteur 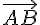\vec{AB}, notée ||\,\vec{AB}\,||,  est définie par \,||\,\vec{AB}\,||=AB.

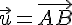
Soit \vec{u} un vecteur du plan et deux points A et B tels que \vec{u}=\vec{AB}.

La norme de \vec{u} est alors définie par ||\,\vec{u}\,||=AB.

Propriété :

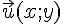
Soit \vec{u}(x;y) dans un repère orthonormé alors ||\,\vec{u}\,||=\,\sqrt{x^2+y^2}.

Pour tout réel k, ||k\,\vec{u}|\|=\,|k|\times ||\,\vec{u}\,||.

Autre version de cette leçon

I. Vecteurs directeurs et équation cartésienne

Dans tout ce chapitre, on se place dans un repère orthonormé 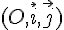(O,\vec{i},\vec{j}).

1.Vecteur directeur d’une droite.

Définition :

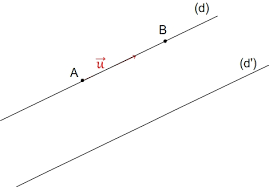
On appelle vecteur directeur d’une droite (d) tout représentant du vecteur 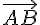\vec{AB} où

A et B sont deux points quelconques et distincts de la droite (d).

Exemple :

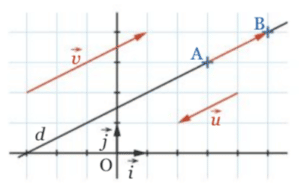
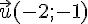
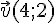
Dans l’image ci-dessous, les vecteurs \vec{AB}(2;1), \vec{u}(-2;-1) et \vec{v}(4;2) sont des vecteurs

directeurs de la droite (d).

vecteur directeur

Application et méthode :
  1. On calcule les coordonnées d’un vecteur directeur de la droite.
  2. La droite (BC) et sa parallèle ont les mêmes vecteurs directeurs, il suffi d’en prendre un représentant d’origine A.

Exemple :

Soient trois points A(1;5), B(-3;2) et C(2;-1) dans un repère orthonormé.

  1. Déterminer un vecteur directeur de la droite (BC).
  2. Détailler la construction de la parallèle à (BC) passant par A.

2. Equation cartésienne de droite.

Théorème :

Dans un repère orthonormé, les coordonnées de l’ensemble des points 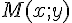M(x;y)

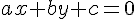
d’une droite vérifient une relation ax+by+c=0 où a, b et c sont des nombres réels.

Démonstration :

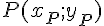
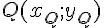
Soient P(x_P;y_P) et Q(x_Q;y_Q)  deux points d’une droite (d).

Alors, pour tout point 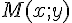M(x;y) appartenant à (d), nous avons :

les vecteurs \vec{PM}(x-x_P;y-y_P) et \vec{PQ}(x_Q-x_P;y_Q-y_P) sont colinéaires.

On a donc det(\vec{PM};\vec{PQ})=0.

C’est-à-dire (x-x_P)(y_Q-y_P)-(y-y_P)(x_Q-x_P)=0.

x(y_Q-y_P)-x_P(y_Q-y_P)-y(x_Q-x_P)+y_P(x_Q-x_P)=0

donc (y_Q-y_P)x+(x_P-x_Q)y+(y_Px_Q-x_Py_Q)=0.

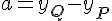
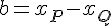
En posant  a=y_Q-y_P;  b=x_P-x_Q  et c=y_Px_Q-x_Py_Q,

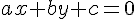
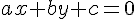
on a donc l’équation de la droite (d) qui est de la forme  ax+by+c=0.

Définition :

La relation ax+by+c=0 s’appelle une équation cartésienne de la droite (d).

Propriété :

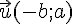
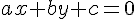
Le vecteur \vec{u}(-b;a) est un vecteur directeur de la droite (d) d’équation cartésienne ax+by+c=0.

Exemple :

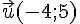
Si la droite (d) a pour équation cartésienne 5x+4y-11=0, alors le vecteur \vec{u}(-4;5)

est un vecteur directeur de cette droite.

II. Positions relatives de droites

1.Droites parallèles ou sécantes

Théorème :

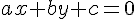
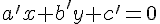
Soient deux droites (d) et (d’) d’équations cartésiennes respectives ax+by+c=0 et a'x+b'y+c'=0 où a,b,c,a',b',c' sont des nombres réels.

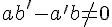
Les droites (d) et (d’) sont parallèles si, et seulement si, ab'-a'b\neq0.

Preuve :

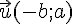
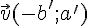
Des vecteurs directeurs des droites (d) et (d’) sont, respectivement, \vec{u}(-b;a) et \vec{v}(-b';a').

Les droites (d) et (d’) sont sécantes si, et seulement si, les vecteurs \vec{u} et \vec{v} ne sont pas colinéaires.

Autrement dit, si le déterminant de ces deux vecteurs est non nul.

Soit, -ba'-(a(-b'))=-ba'+ab'=ab'-a'b\neq0.

2. Droites sécantes et systèmes d’équation

Théorème :

Lorsque deux droites sont sécantes, les coordonnées 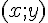(x;y) de leur point d’intersection

sont solution du système :

système d'équations

3. Droites perpendiculaires

Théorème :

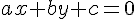
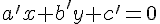
Soient deux droites (d) et (d’) d’équations cartésiennes respectives ax+by+c=0 et a'x+b'y+c'=0 où a,b,c,a',b',c' sont des nombres réels.

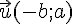
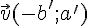
Les vecteurs directeurs des droites (d) et (d’) sont, respectivement, \vec{u}(-b;a) et \vec{v}(-b';a').

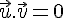
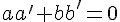
Les droites (d) et (d’) sont perpendiculaires si, et seulement si, \vec{u}.\vec{v}=0 soit aa'+bb'=0.

Preuve :

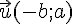
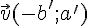
Les vecteurs directeurs des droites (d) et (d’) sont, respectivement, \vec{u}(-b;a) et \vec{v}(-b';a').

Les droites sont perpendiculaires si, et seulement si, ces deux vecteurs directeurs sont orthogonaux.

Ce qui revient à dire que le produit scalaire de ces deux vecteurs est nul, soit :

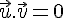
\vec{u}.\vec{v}=0

Ce qui équivaut à :

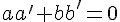
-b\times \,(-b')+a\times \,a'=0 soit aa'+bb'=0.

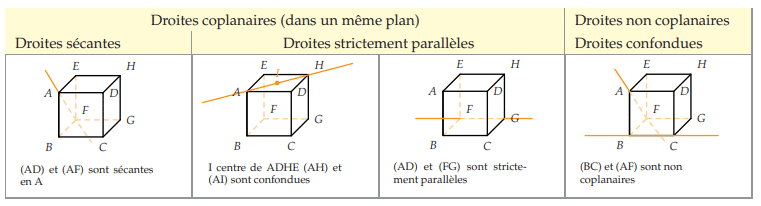
I. Positions relatives de droites et plans en géométrie

Propriété : positions relatives de deux droites
Deux droites de l’espace sont soit coplanaires (c’est-à-dire qu’il existe un plan les contenant
toutes les deux), soit non coplanaires (c’est-à-dire qu’il n’existe aucun plan les contenant
toutes les deux).
Si elles sont coplanaires, alors elles sont soit sécantes, soit parallèles (strictement parallèles
ou confondues).

Position relative de deux droites 1

Propriété : Positions relatives de deux plans.
Deux plans de l’espace sont soit sécants (leur intersection est une droite), soit parallèles.
Propriété : Positions relatives d’une droite et d’un plan.
Une droite et un plan de l’espace sont soit sécants, soit parallèles.

position relative plan droite

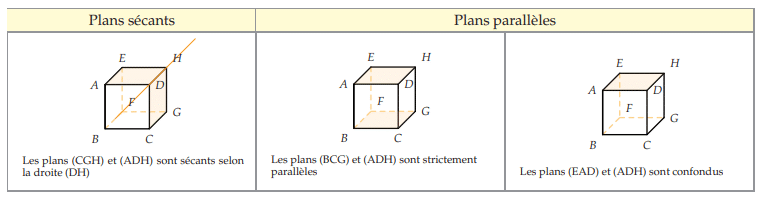
II. Parallélisme dans l’espace

Propriété :
Si deux droites sont parallèles à une même droite alors elles sont parallèles entre elles.
Si deux plans sont parallèles à un même plan alors ils sont parallèles entre eux.
Propriété :
Une droite est parallèle à un plan si et seulement si elle est parallèle à une droite de ce plan.
Propriété :
Si un plan P contient deux droites sécantes respectivement parallèles à deux droites sécantes
d’un plan P’ alors les plans P et P’ sont parallèles.

plans parallèles

Propriété :
Si deux plans sont parallèles, alors tout plan qui coupe l’un coupe l’autre et les droites
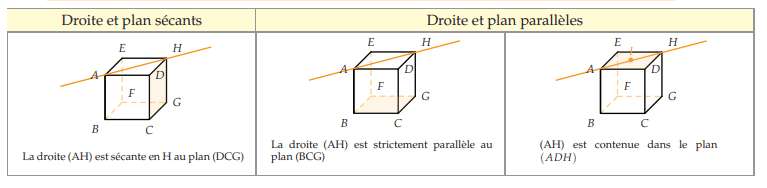
d’intersection sont parallèles entre elles.
Propriété : Théorème du toit.
Soit P et P’ deux plans distincts, sécants selon une droite ∆.
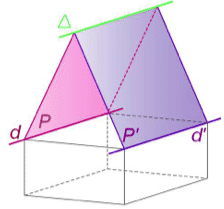
Si une droite d de P est strictement parallèle à une droite d’ de P’ alors la droite ∆
intersection de P et P’ est parallèle à d et à d’.

théorème toit

4.1/5 - (32073 votes)

À propos de l’auteur

Professeur de maths

Enseignant titulaire en mathématiques de l'Éducation Nationale depuis 2001.
Spécialisé en pédagogie au collège et lycée et préparation au brevet et au baccalauréat.
✓ 24 ans d'expérience • ✓ Expert pédagogie différenciée

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «vecteurs, droites et plans : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Ressources mathématiques de Première

Cours de Première

Exercices de Première

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Nombre de fichiers PDF téléchargés.  Maths PDF c'est 13 775 153 cours et exercices de maths téléchargés en PDF et 4 250 exercices.