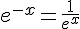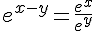Fonction exponentielle : cours de maths en 1ère à imprimer en PDF.

Mis à jour le 20 décembre 2025

Sommaire

📚Cours de MathématiquesPremière • lycée

Fonction exponentielle

⏱️Temps de lecture : 3 min

🎯Difficulté : Avancé

📚Cycle terminal

📋Prérequis : Programme 2nde maîtrisé

📄Format PDF disponible gratuitement

La fonction exponentielle à travers un cours de maths en 1ère complet. Vous devrez connaître l’ensemble de définition de cette fonction ainsi que sa dérivée. Appliquer les différentes formulés de calculs et savoir calculer des limites en un point ou en l’infini. Étudiez la courbe et son sens de variation afin de pouvoir la tracer en terminale.

I.La fonction exponentielle

Lemme :

Si il existe une fonction f dérivable sur

telle que

et f(0)=1 alors f ne s’annule pas sur

Théorème :

Il existe une unique fonction f dérivable sur telle que

et f(0)=1.

Définition :

On appelle fonction exponentielle, notée exp, l’unique fonction dérivable sur R et telle que 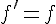f'=f et f(0)=1.Nous noterons cette fonction définie par et e^0=1 .

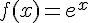
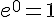
II.Les propriétés de la fonction exponentielle

Théorème :

On considère deux nombres réels x et y.Nous avons 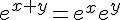$e^{x+y}=e^xe^y$ .

Exemple :

$e^{5+2}=e^5e^2$

Propriétés :

On considère deux nombres réels x et y et n un entier naturel.Nous avons les propriétés suivantes :

$e^{-x}=\frac{1}{e^x}$ ;
$e^{x-y}=\frac{e^x}{e^y}$ ;
$e^{nx}=(e^x)^n$

Exemple :

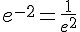
$e^{-2}=\frac{1}{e^2}$

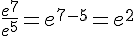
$\frac{e^7}{e^5}=e^{7-5}=e^2$

III.Etude de la fonction exponentielle

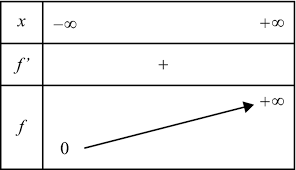
1.Le signe et ses variations

Propriété :

On considère la fonction définie et dérivable sur $\mathbb{R}$ par .

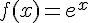
f est continue sur $\mathbb{R}$ ;
f est strictement positive sur $\mathbb{R}$ ;
f est strictement croissante sur $\mathbb{R}$ .

2.Les limites en l’infini

Propriété :

On considère la fonction définie et dérivable sur $\mathbb{R}$ par .

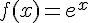
Nous avons $\lim_{x\rightarrow\,+\infty}f(x)=+\infty$ et $\lim_{x\rightarrow\,-\infty}f(x)=0^+$ .

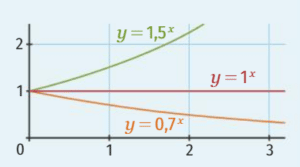
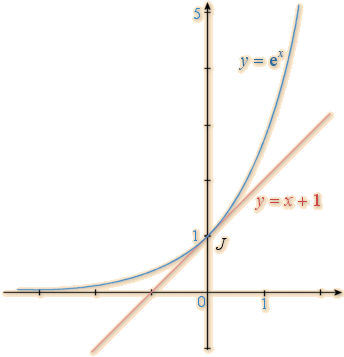
3.Tableau de variation et courbe représentative

Propriété :

On considère la fonction définie et dérivable sur $\mathbb{R}$ par .

Remarques :

La droite d’équation y=0 est une asymptote horizontale à la courbe de la fonction exponentielle en $-\infty$ .

La droite d’équation y=x+1st une asymptote oblique à la courbe de la fonction exponentielle en 0.

3.Equations et inéquations

Propriété :

On considère deux nombres réels x et y.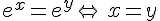 $e^x=e^y\Leftrightarrow\,x=y$

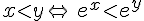
$x<y\Leftrightarrow\,e^x<e^y$

4.8/5 - (32385 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonction exponentielle : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Cours de Première

Fonctions trigonométriques

Suites numériques

Les équations et les inéquations du second degré

Produit scalaire dans le plan

Exercices de Première

vecteurs droites plan exercices maths 1ere

Vecteurs et droites du plan

Dérivée

Les suites

produit scalaire plan exercices maths 1ere

Produit scalaire dans le plan

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

Scratch Heroes : escape game de programmation avec Scratch.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 553 587 cours et exercices de maths téléchargés en PDF et 4 250 exercices.