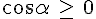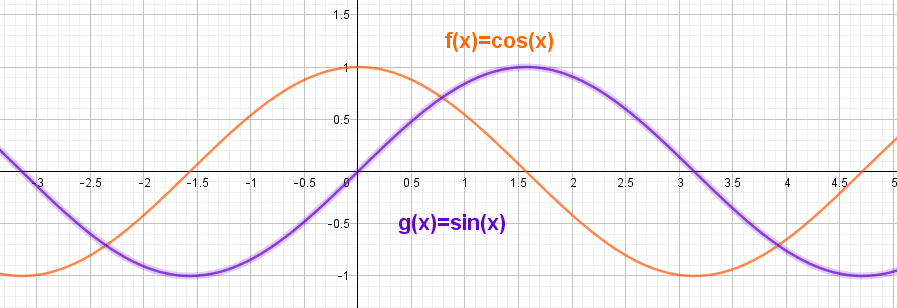Fonctions trigonométriques : cours de maths en 1ère à imprimer en PDF.
Mis à jour le 20 décembre 2025
Les fonctions trigonométriques à travers un cours de maths en 1ère. Nous aborderons le repérage sur le cercle trigonométrique et sa définition. L’élève devra connaître la définition du radian ainsi que des fonctions cosinus et sinus ainsi que leurs différentes valeurs remarquables en première.
Dans tout le chapitre on se place dans le plan muni d’un repère orthonormé (O ; l, J).
La droite numérique Peut également être appelée droite des réels.
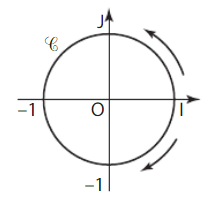
I. Repérage sur le cercle trigonométrique
et de rayon r = 0I=1.
Le périmètre P du cercle trigonométrique est égal à :
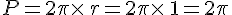
• le sens direct (ou positif ou encore trigonométrique) est contraire au sens de rotation des aiguilles
d’ une montre ;
• le sens indirect (ou négatif) est le sens de rotation des aiguilles d’une montre.
Exemple :
Le panneau de signalisation ci-dessous sert à indiquer le sens de parcours à prendre lors
de l’abord d’un carrefour giratoire. Le sens utilisé est le sens trigonométrique.
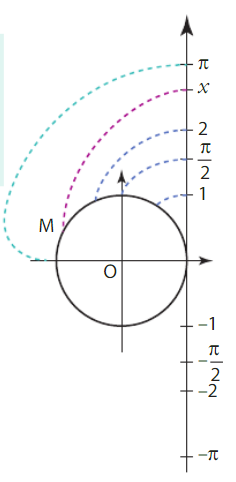
cercle un axe vertical orienté vers le haut, gradué, d’origine le point I.On peut alors associer un réel x à ce point M, x étant l’abscisse d’un point de l’axe qui
Vient se superposer au M.On dit alors que ce point M est le point-image de x sur le cercle trigonométrique, ce que l’on peut noter
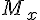
- Lorsqu’on enroule l’axe dans le sens direct, ce sont des points d’abscisses positives qui se superposent à M ; dans le sens indirect, ce sont des d’abscisses négatives.
- Tout point sur le cercle trigonométrique se repère par plusieurs nombres réels,
distants d’un multiple de
nombre de tours complets de l’enroulement de l’axe.
Exemples :
- Les points de la droite des réels O ;
image le même point à savoir I. - Les points
Remarque :
- A chaque réel x on associe un point M sur le cercle trigonométrique.
- Ce réel x est lié à l’angle au centre et donc la longueur d’arc de cercle trigonométrique associée.
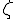
La mesure en radian de l’angle
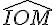
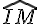
Le symbole associé à cette mesure est rad ou rd.

Remarques :
• Dans ces conditions, 360° correspondent à 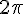
(E = I rad
• Par proportionnalité, on obtient que 30° correspondent à 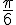
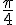
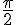
• II faut faire attention au paramétrage de sa calculatrice selon le mule degré ou radian choisi.
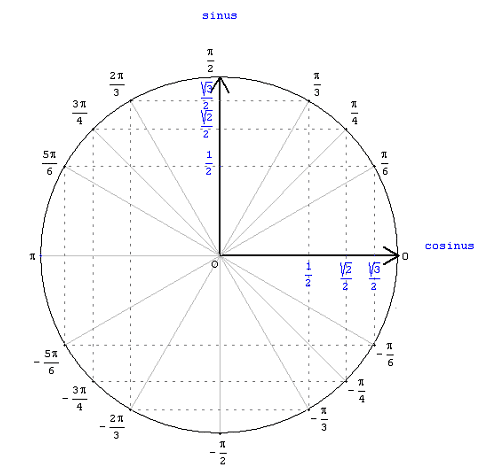
II. Coordonnées d’un point du cercle trigonométrique
1.Sinus et cosinus
image de x sur le cercle trigonométrique. On écrit alors
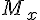
Exemples :
Le réel 0 est associé au point I sur le cercle trigonométrique.
On obtient donc cos(0)= 1 et sin(0) = 0.
Le réel 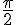
On obtient donc 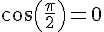
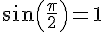
Pour tout nombre réel x :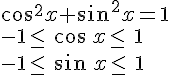
Démonstration :
Soit M le point associé au réel x.
Le repère est orthonormé, on obtient donc la formule suivante :
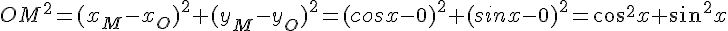
Or, le cercle trigonométrique est de rayon 1, donc 0M =1, donc OM²= 1, donc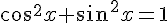
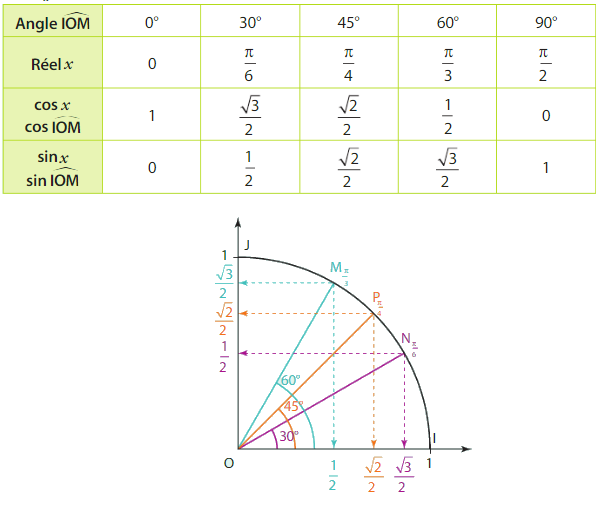
2. Valeurs remarquables
Soit M un point du cercle trigonométrique, image d’un réel x. Alors :
Démonstrations :
On appelle H le pied de la hauteur issue de M dans le triangle OMI.
1. Calcul de 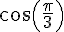
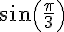
Si 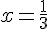
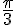
équilatéral. Dans un triangle équilatéral, la médiane et la hauteur sont confondues, donc H est le milieu du segment [OI] de longueur 1, donc 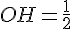
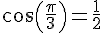
En appliquant le théorème de Pythagore au triangle OHM rectangle en H, on obtient :
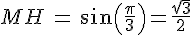
2.Calcul de 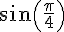
Si 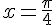
On obtient donc la relation 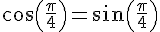
En appliquant le théorème de Pythagore au sein du triangle OHM, on obtient :
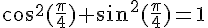
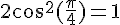
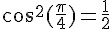
Comme 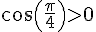
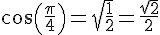
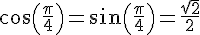
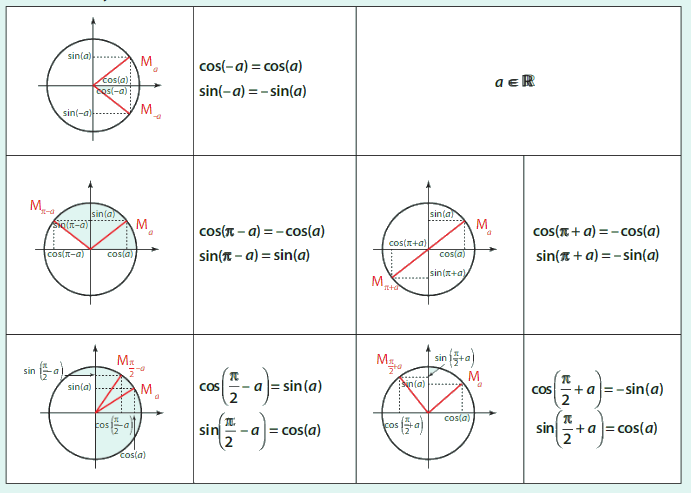
3.Angles associés
III. Fonctions cosinus et sinus
• La cosinus, notée cos, est la fonction définie sur 
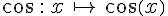
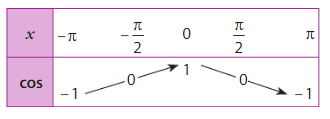
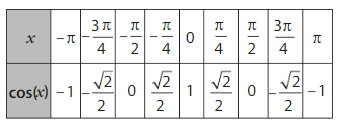
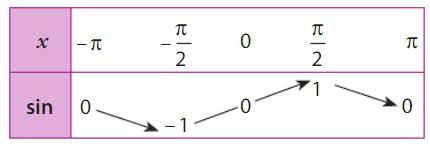
• Un tableau de valeurs de la fonction cosinus est :
• Un tableau de variations de la fonction cosinus sur ![]-\pi;\pi]](https://maths-pdf.fr/latex-images/a693574a43f0291195eadc5321437c55.png)
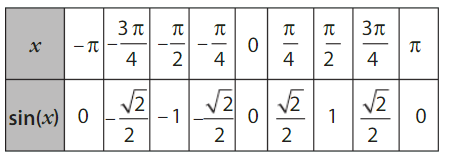
• La fonction sinus, notée sin, est la fonction définie sur 
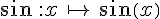
Remarques :
• Les fonctions sinus et cosinus sont des fonctions trigonométriques.
• Les fonctions trigonométriques servent modéliser des phénomènes dits superposition de points-images
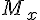
et
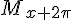
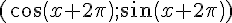
Démonstration :
Le périmètre du cercle trigonométrique est égal à 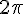
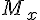
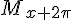
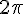
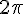
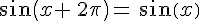
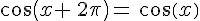
Soit un réel x. Alors :
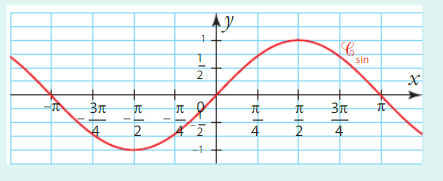
- la fonction sinus est impaire. Sa courbe représentative est alors symétrique par rapport å l’origine
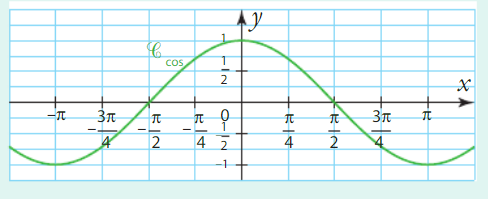
du repère. - la fonction cosinus est paire. Sa courbe représentative est alors symétrique par rapport l’axe des
ordonnées du repère.
Les courbes 
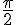
En effet, 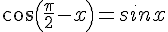
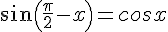
IV. Signe du sinus et du cosinus.
Par définition, le sinus et le cosinus de tout nombre réel appartiennent à l’intervalle [-1 ; 1].
Plus précisément, la position de M nous permet d’en savoir plus sur le cosinus et le sinus de 
- Si
- Si
V.Visualisation des sinus et cosinus sur le cercle trigonométrique.
C’est un outil indispensable, qu’il est utile de bien visualiser afin d’être capable de retrouver rapidement les valeurs indiquées ci-dessous.
VI.Formules usuelles concernant les angles associés.
La fonction cosinus est donc paire et la fonction sinus est impaire.
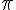
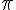
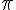
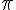
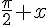
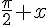
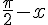
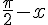
VII. Représentations graphiques des fonctions sinus et cosinus
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «fonctions trigonométriques : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Première
Exercices de Première
Nos applications
Téléchargez la dernière version gratuite de nos applications.


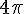
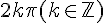
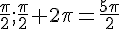
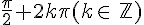
![\alpha\,\in[0+2k\pi,\pi+\,2k\pi]](https://maths-pdf.fr/latex-images/3759e52270694a5ea1c1a7044362c8a4.png)
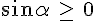
![\alpha\,\in[-\frac{\pi}{2}+2k\pi,\frac{\pi}{2}+\,2k\pi]](https://maths-pdf.fr/latex-images/32ffd7ec4a07761d2e9a60abd369add3.png)