Produit scalaire dans le plan : cours de maths en 1ère à imprimer en PDF.
Mis à jour le 20 décembre 2025
I. Norme d’un vecteur
Soit 


a. On appelle norme du vecteur 
, le nombre
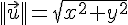
b. Si est 
.
II. Critère d’orthogonalité de deux vecteurs
Soient 

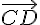
Les vecteurs 

On note dans ce cas 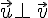
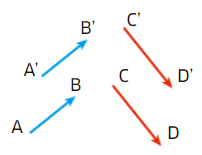
Remarque :
La définition ne dépend pas des représentants des vecteurs.
En effet, Si 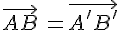
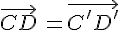
alors
.
III.Définition du produit scalaire et orthogonalité
On considère deux vecteurs du plan 

Le produit scalaire de 

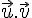
.
Remarque :
Le produit scalaire n’est pas un vecteur mais un nombre réel.
Le produit scalaire est commutatif, c’est à dire que 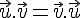
Si 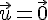
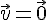
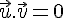
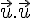
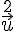

Nous avons .
On considère deux vecteurs non nuls du plan 

On dit que deux vecteurs 

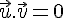
Remarque :
Le vecteur nul est donc orthogonal à tout vecteur du plan.
On considère deux vecteurs non nuls du plan 



![(\vec{u};\vec{v})=\pm\,\frac{\pi}{2}[2\pi]](https://maths-pdf.fr/latex-images/24f0d567a5958879e627968a69374a15.png)
IV.Produit scalaire et coordonnées
Soient 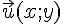
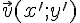


.
V. Propriétés algébriques du produit scalaire
- Le produit scalaire est distributif par rapport à l’addition :
.
- Pour deux réels k et k’,
.
- En particuliers,
.
.
.
.
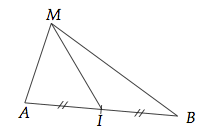
Soient A et B deux points distincts du plan et I le milieu de [AB].
Pour tout point M du plan, .
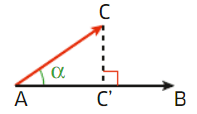
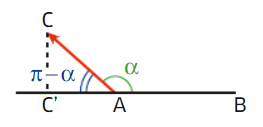
VI.Autres expressions du produit scalaire
On considère deux vecteurs non nuls du plan 

.
.
Si deux vecteurs du plan 

si
si
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «produit scalaire dans le plan : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Première
Exercices de Première
Nos applications
Téléchargez la dernière version gratuite de nos applications.