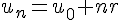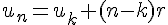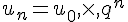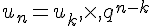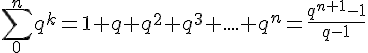Suites numériques : cours de maths en 1ère à imprimer en PDF.
Mis à jour le 20 décembre 2025
I.Mode de génération d’une suite numérique
Une suite numérique est une fonction de 


On l’appelle terme d’indice n de la suite.
Cette suite est notée 
Définir une suite par une relation de récurrence, c’est donner le premier terme de la suiteet une méthode de calcul de 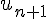

Exemple :
Soit la suite 
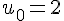
.
II. Diverses manières de définir une suite
1. Suites définies par une égalité fonctionnelle
Une suite numérique étant une fonction définie sur 




Par exemple, la suite 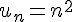




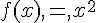
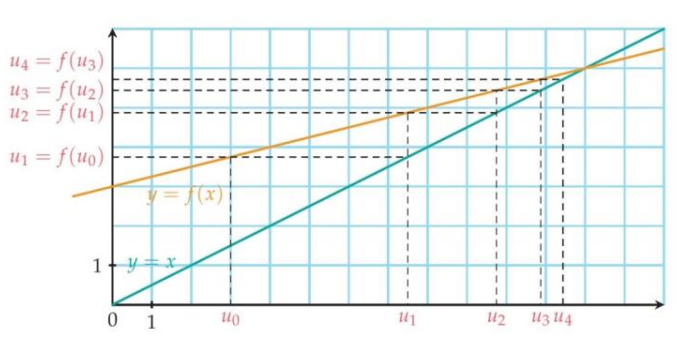
2.Suite définie par une formule de récurrence
La spécificité des suites sur les fonctions de la variable réelle, est que, pour tout entier naturel n, son image 
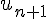

Plus précisément, la suite 
– Son premier terme 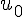
– Une égalité reliant deux termes consécutifs quelconques de la suite .
Exemple :
Par exemple, la suite définie par son premier terme 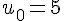
.
III.Les suites arithmétiques
On dit qu’une suite 
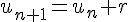
Le réel r est appelé raison de la suite arithmétique 
- Si
- Si
La somme des n premiers entiers est donnée par :
La somme des n premiers termes d’une suite arithmétiques de raison 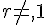
.
IV.Les suites géométriques
On dit qu’une suite 
.
Le réel q est appelé raison de la suite géométrique 
- Si
- Si
Pour tout réel q non nul et différent de 1,
Exemples:
- La suite des entiers naturels est la suite arithmétique de premier terme 0 et de raison 1.
- La suite des entiers naturels pairs est la suite arithmétique de premier terme 0 et de raison 2.
- La suite des entiers naturels impairs est la suite arithmétique de premier terme 1 et de raison 2.
- La suite définie par la formule: Un = an + b (fonction affine de n) est la suite arithmétique de premier terme U0 = b et de raison a.
- La suite constante de terme général Un = 2 est la suite géométrique de premier terme 2 et de raison 1.
- La suite de terme général Un = (-1)n est la suite géométrique de premier terme U0 = 1 et de raison -1.
- La suite des puissances d’un nombre réel a non nul, de terme général Un = an est la suite géométrique de premier terme U0 = 1 et de raison a.
- La suite définie par la formule: Un = a bn (fonction exponentielle de n) est la suite géométrique de premier terme U0 = a et de raison b (b réel non nul).
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «suites numériques : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Première
Exercices de Première
Nos applications
Téléchargez la dernière version gratuite de nos applications.