Simulation et échantillonnage : corrigé des exercices de maths en 2de en PDF

Mis à jour le 24 novembre 2025

Dans le cadre des mathématiques en seconde, la simulation et l’échantillonnage sont des concepts essentiels qui permettent aux élèves de développer des compétences clés en statistiques et en probabilités. Comprendre ces notions aide non seulement à réaliser des exercices pratiques, mais aussi à analyser des situations réelles avec discernement. Ce guide de corrections d’exercices vous fournira des outils indispensables pour maîtriser ces compétences et réussir dans votre parcours scolaire.

Exercice 1 – composants électroniques et fréquence.

a) Pour n = 1600, quelle est la longueur de I ?

On utilise la formule de l’intervalle de fluctuation à 95 % :

$I\ =\ [p\ -\ 1,96\ \times \ \sqrt{\frac{p\ \times \ (1-p)}{n}},\ p\ +\ 1,96\ \times \ \sqrt{\frac{p\ \times \ (1-p)}{n}}]$

Où p = 0,04 et n = 1600.

Calculons l’écart :

$1,96\ \times \ \sqrt{\frac{0,04\ \times \ 0,96}{1600}}\ \approx\ 0,0098$

La longueur de l’intervalle $ I $ est donc :

$2\times 0,0098\ =\ 0,0196$

b) Pour quelle valeur de n la longueur de I est-elle deux fois plus petite ?

Nous voulons que :

$0,0196\ :\ 2\ =\ 0,0098$

Utilisons la formule de l’écart avec n inconnu :

$1,96\ \times \ \sqrt{\frac{0,04\ \times \ 0,96}{n}}\ =\ 0,0049$

En résolvant pour n, on trouve :

Après simplification :

$n\ =\ \frac{0,04\ \times \ 0,96\ \times \ (1,96)^2}{(0,0049)^2}$

Effectuons les calculs :

$n\ \approx\ 6400$

Exercice 2 – lancer de dé et fréquence d’obtention.

Voici un algorithme simple pour simuler 50 lancers de dé :

Initialiser un compteur à 0.
Pour chaque lancer de 1 à 50 :
1. Générer un nombre aléatoire entre 1 et 6.
2. Si le nombre est supérieur ou égal à 5, ajouter 1 au compteur.

La fréquence d’obtention d’un numéro supérieur ou égal à 5 est calculée par :

$\frac{\text{Compteur de lancers reussis}}{50}$

En supposant un code Python :

import random

compteur = 0

for _ in range(50):
    lancer = random.randint(1, 6)
    if lancer >= 5:
        compteur += 1

frequence = compteur / 50

print("Fréquence d'obtention d'un numéro supérieur ou égal à 5 :", frequence)

Exécution typique en programmant peut afficher une fréquence autour de :

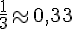
$\frac{1}{3}\approx0,33$

Exercice 3 – champ de fleur et algorithme pour simuler un échantillon.

a) Conception de l’algorithme :

Pour simuler un échantillon de 45 fleurs :

Initialiser fleurs_jaunes à 0
Initialiser fleurs_bleues à 0

Pour i allant de 1 à 45 :
    Générer un nombre aléatoire entre 0 et 1
    Si le nombre < 0,4 :
        Incrémenter fleurs_jaunes de 1
    Sinon :
        Incrémenter fleurs_bleues de 1

Afficher fleurs_bleues

b) Modification de l’algorithme :

Pour saisir la taille de l’échantillon :

Lire taille_échantillon
Initialiser fleurs_jaunes à 0
Initialiser fleurs_bleues à 0

Pour i allant de 1 à taille_échantillon :
    Générer un nombre aléatoire entre 0 et 1
    Si le nombre < 0,4 :
        Incrémenter fleurs_jaunes de 1
    Sinon :
        Incrémenter fleurs_bleues de 1

Afficher fleurs_bleues

Exercice 4 – formule de tableur et intervalle.

a) =ALEA() affiche un nombre aléatoire dans l’intervalle .

b) =ALEA()+0,65 affiche un nombre dans l’intervalle .

c) =ALEA()+\frac{1}{4} affiche un nombre dans l’intervalle .

Exercice 5 – tableur et probabilité.

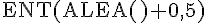
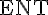
a) Pour la formule $\text{ENT(ALEA()+0,5)}$ :

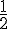
La probabilité que $\text{ENT}$ soit égale à 1 est $\frac{1}{2}$ , donc 0,5.

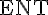
La probabilité que $\text{ENT}$ soit égale à 0 est 0,5.

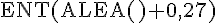
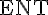
b) Pour la formule $\text{ENT(ALEA()+0,27)}$ :

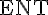
La probabilité que $\text{ENT}$ soit égale à 1 est 0,73.

La probabilité que $\text{ENT}$ soit égale à 0 est 0,27.

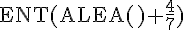
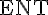
c) Pour la formule $\text{ENT(ALEA()+\frac{4}{7})}$ :

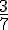
La probabilité que $\text{ENT}$ soit égale à 1 est $\frac{3}{7}$ , donc 0,43.

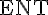
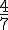
La probabilité que $\text{ENT}$ soit égale à 0 est $\frac{4}{7}$ , donc 0,57.

Exercice 6 – sac d’haricots et tableur pour simuler un échantillon.

a) Explication de la formule :

La formule =ENT(ALEA()+0,6) utilise la fonction ENT, qui renvoie la partie entière d’un nombre, et ALEA(), qui génère un nombre aléatoire entre 0 et 1. En ajoutant 0,6, on simule une probabilité de 60 % d’obtenir un haricot blanc (valeur 1) et 40 % d’obtenir un haricot rouge (valeur 0).

b) Simulation avec le tableur :

Pour simuler un échantillon de 38 haricots, on peut copier la formule =ENT(ALEA()+0,6) dans 38 cellules d’une colonne. Les valeurs obtenues (0 ou 1) représentent respectivement les haricots rouges et blancs extraits du sac.

c) Calcul de la fréquence des haricots blancs :

La fréquence des haricots blancs dans l’échantillon est calculée en divisant le nombre de 1 obtenus par 38. Par exemple, si on obtient 24 haricots blancs, la fréquence est :

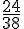
$\frac{24}{38}$

Cette fréquence n’est pas nécessairement égale à 0,6 en raison de la variabilité inhérente à l’échantillonnage aléatoire. Avec un nombre d’essais relativement faible, il est normal d’observer des écarts par rapport à la probabilité théorique de 60 %.

Exercice 7 – une boîte de perles et fréquence de cet échantillon.

a) Simulation d’un collier :

Pour simuler un collier avec la calculatrice, vous pouvez générer 45 nombres aléatoires entre 1 et 100. Comptez-les comme perles dorées si le nombre est compris entre 1 et 75, et comme perles argentées si le nombre est entre 76 et 100.

b) Calcul de la fréquence des perles dorées :

Calculez la fréquence des perles dorées en divisant le nombre de perles dorées par le nombre total de perles (45).

Exemple : Supposons que 33 des 45 perles sont dorées, alors la fréquence est :

$\frac{33}{45} \approx 0,733$

Cette fréquence n’est pas nécessairement égale à 0,75 car nous avons ici un échantillon de petite taille par rapport à la totalité des perles.

Les variations aléatoires peuvent donc affecter le résultat.

Exercice 8 – montures de lunettes et intervalle de fluctuation.

1. Calculons l’écart-type pour un échantillon de taille 50.

Pour cela, utilisons la formule de l’écart-type pour une proportion :

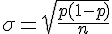
$\sigma=\sqrt{\frac{p(1-p)}{n}}$

où p = 0,38 et n = 50.

$\sigma=\sqrt{\frac{0,38(1-0,38)}{50}} \approx 0,0693$

2. Pour un intervalle de fluctuation à 95 %, il nous faut 1,96 écarts-types de part et d’autre de la moyenne :

$0,38 \pm 1,96 \times 0,0693$

Calculons cela :

Limite inférieure :

$0,38-1,96\times 0,0693 \approx 0,244$

Limite supérieure :

$0,38+1,96\times 0,0693 \approx 0,516$

Conclusion : L’intervalle de fluctuation au seuil de 95 % est $[0,244 ; 0,516]$

Exercice 9 – des céréales et des lentilles avec intervalles de fluctuation.

a) Calcul des intervalles de fluctuation :

Pour un échantillon de taille 100, la fréquence théorique du blé est 0,58 et celle de l’épeautre est 0,22.

La formule pour calculer un intervalle de fluctuation au seuil de 95 % est :

$[p - 1,96\times \sqrt{\frac{p(1-p)}{n}}\,;\,p + 1,96\times \sqrt{\frac{p(1-p)}{n}}]$

Pour le blé :

$p=0,58,\ n=100$

$[0,58 - 1,96\times \sqrt{\frac{0,58\times 0,42}{100}}\,;\,0,58 + 1,96\times \sqrt{\frac{0,58\times 0,42}{100}}]$

Pour l’épeautre :

$p=0,22,\ n=100$

$[0,22 - 1,96\times \sqrt{\frac{0,22\times 0,78}{100}}\,;\,0,22 + 1,96\times \sqrt{\frac{0,22\times 0,78}{100}}]$

b) Justification pour le riz rouge et les lentilles :

On ne peut pas utiliser la formule pour le riz rouge (10 %) et les lentilles (10 %) car la condition $n \geq\, 30$

et $n \times p \times (1 - p) > 5$ n’est pas respectée.

En effet, $100 \times 0,10 \times 0,90 = 9$ , qui est trop petit pour appliquer cette formule de manière fiable.

Exercice 10 – déformation du crâne et proportions.

Calculons d’abord la proportion de bébés présentant une déformation du crâne :

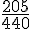
$\frac{205}{440}$

Cette fraction se simplifie pour donner :

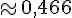
$\approx0,466$

Cela correspond à environ 47%.

Cette étude amène donc à rejeter une proportion de :

a) 50%

b) 61%

mais pas :

c) 3%

4.9/5 - (36850 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «simulation et échantillonnage : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Systèmes de deux équations à deux inconnues

Probabilités

Statistiques

Inéquations

Intervalles et valeur absolue

L’étude de fonction

Les équations de droites

Géométrie dans l’espace

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 357 910 cours et exercices de maths téléchargés en PDF et 4 250 exercices.