Systèmes de deux équations à deux inconnues : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Exercice 1 – résoudre le système.
Étape 1 : Exprimer y en fonction de x à partir de la première équation :

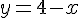
Étape 2 : Remplacer y dans la deuxième équation :
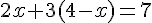
Étape 3 : Développer et simplifier :
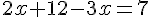
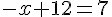
Étape 4 : Résoudre pour x :

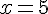
Étape 5 : Trouver y en utilisant y=4-x :
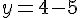
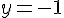
Exercice 2 – résolution de système.
Nous allons résoudre le système suivant :
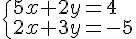
Étape 1 : Exprimer x en fonction de y à partir de la première équation.
De la première équation, nous avons :
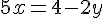
Donc :

Étape 2 : Remplacer x dans la deuxième équation.
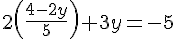
En simplifiant, nous avons :
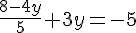
Multipliant toute l’équation par 5 pour éliminer le dénominateur :
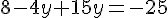
En simplifiant :
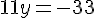
Donc :
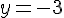
Étape 3 : Calculer x en utilisant la valeur de y.
Substituer y dans l’expression de x :
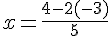
Ce qui donne :
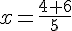
Donc :
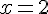
Conclusion : La solution du système est :
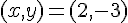
Exercice 3 – trouver l’ensemble solution.
Étape 1 : Isoler x dans la première équation.
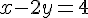
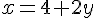
Étape 2 : Remplacer x dans la deuxième équation.


Étape 3 : Développer et simplifier.
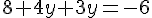
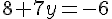
Étape 4 : Résoudre pour y.
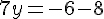

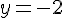
Étape 5 : Trouver la valeur de x.
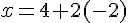
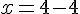
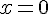
L’ensemble solution est 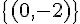
Exercice 4 – déterminer le couple solution.
Pour résoudre le système d’équations suivant :
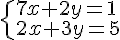
Étape 1 : Exprimons x en fonction de yà partir de la première équation.
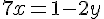
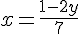
Étape 2 : Remplaçons x dans la deuxième équation.

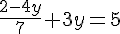
Étape 3 : Résolvons pour y.
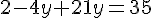
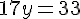

Étape 4 : Trouvons x en substituant y dans l’équation obtenue pour x.

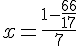


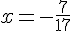
Le couple solution est 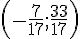
Exercice 5 – une infinité de solution.
Pour montrer qu’un système a une infinité de solutions, il faut que les deux équations soient équivalentes,
c’est-à-dire que l’une puisse se déduire de l’autre par une multiplication.
Considérons les équations suivantes :
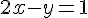
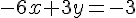
Multiplions la première équation par 3 :

Ce qui donne :

Maintenant prenons l’équation 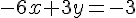
Si nous la multiplions par -1, nous obtenons :

Les deux équations 
ce qui signifie que le système a une infinité de solutions.
Exercice 6 – des lapins et des poules dans une ferme.
Soit :
x : le nombre de lapins
y : le nombre de poules
Nous avons les équations suivantes :
1. Les têtes : 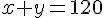
2. Les pattes : 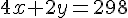
Résolvons ces équations :
De l’équation 1, nous trouvons : 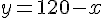
Substituons dans l’équation 2 : 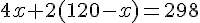
Développons : 
Simplifions : 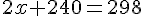
Retirons 240 des deux côtés : 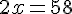
Divisons par 2 : 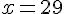
En substituant x = 29 dans l’équation de y : 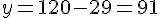
Conclusion : Il y a 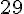
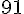
Exercice 7 – panier avec des pommes et des carottes.
Appelons x le prix d’un kg de pommes et y le prix d’un kg de carottes.
Pour le panier de Mme Martin :
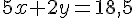
Pour le panier de M. Bernard :
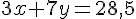
Résolvons ce système d’équations :
Multiplions la première équation par 7 :
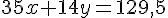
Multiplions la deuxième équation par 2 :
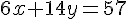
Soustrayons ces deux équations :
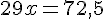

Le prix d’un kg de pommes est 2,5 €.
Substituons x = 2,5 dans la première équation :

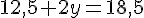
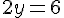
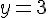
Le prix d’un kg de carottes est 3 €.
Conclusion : Le prix d’un kg de pommes est 2,5 € et le prix d’un kg de carottes est 3 €.
Exercice 8 – des pièces dans un porte-monnaie.
Énoncé : Max a 10 pièces dans son porte-monnaie.
Ce sont uniquement des pièces de 1 € et 2 €.
Le montant contenu dans le porte-monnaie est de 15 €.
Combien a-t-il de pièces de chaque sorte ?
Soit 

Nous avons les équations suivantes :

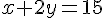
En soustrayant la première équation de la deuxième, nous obtenons :
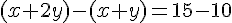
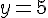
En remplaçant 
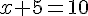
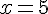
Max a donc 5 pièces de 1 € et 5 pièces de 2 €.
Exercice 9 – système à deux inconnue plus complexe.
Pour résoudre le système suivant :
Déduisons la première équation de la deuxième pour éliminer 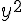
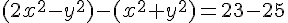
Ce qui donne :
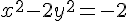
Ajoutons la première équation :
En résolvant :
De la première équation : 
Substituons dans la seconde :
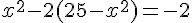
Ce qui donne :
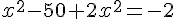
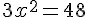


Si 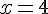
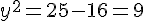

Si 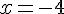
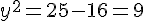

En conclusion, les solutions du système sont :
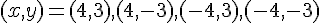
Exercice 10 – résoudre dans R² ce système par substitution.
Commençons par exprimer 
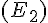
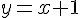
Substituons cette expression de 
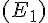

Simplifions cette équation :
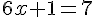
Résolvons pour 

Utilisons cette valeur de 

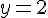
La solution du système est donc 
Télécharger ou imprimer cette fiche «systèmes de deux équations à deux inconnues : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.













