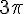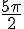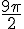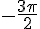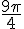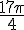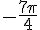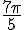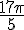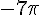Trigonométrie : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Exercice 1 – placer des points sur un cercle trigonométrique.
a) M image de 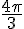
Pour placer M, il faut réduire l’angle modulo 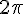
Le point M est donc positionné comme 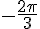
b) N image de 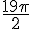
Réduisons également cet angle modulo 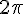
Et encore une fois :
Donc, N est positionné à 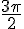
c) P image de 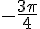
Aucun changement nécessaire car cet angle est déjà compris dans ![[-\pi, \pi]](https://maths-pdf.fr/latex-images/86f9a3a2cc344b78b146c202b2226bae.png)
Le point P est donc positionné à 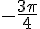
d) R image de 
Réduisons l’angle modulo 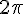
Le point R est donc positionné à 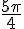
Exercice 2 – image et cercle trigonométrique.
a) M image de 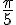
Cet angle se place dans le premier quadrant.
b) N image de 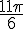
Réduction modulo 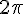

L’angle est dans le quatrième quadrant.
c) P image de 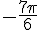
Réduction modulo 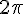
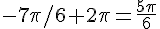
L’angle est dans le deuxième quadrant.
d) R image de 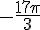
Réduction modulo 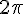
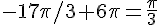
L’angle est dans le premier quadrant.
Exercice 3 – donner des nombres ayant le même point image.
Réponse a) :
- Positifs :
- Négatif :
Réponse b) :
- Positifs :
- Négatif :
Réponse c) :
- Positifs :
- Négatif :
Réponse d) :
- Positifs :
- Négatif :
Exercice 4 – trigonométrie et calculatrice.
a) Valeur approchée :
À l’aide d’une calculatrice, on trouve :
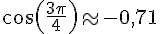
b) Valeurs exactes :
Sur le cercle trigonométrique, l’angle 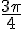
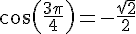
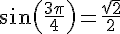
Exercice 5 – calculer une longueur avec la trigonométrie.
a) Calcul de la valeur exacte de OH :
Dans le triangle rectangle OMC, on applique le théorème de Pythagore :
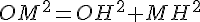
Avec 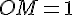



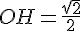
b) Mesure de l’angle 
Dans un triangle isocèle rectangle, les angles sont égaux et valent :
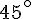
c) Valeurs exactes de 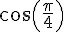
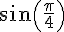
Pour un angle de 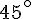
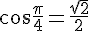
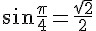
Exercice 6 – déterminer une longueur sur le cercle trigonométrique.
Pour déterminer la longueur de l’arc rouge, nous utilisons la formule de l’arc d’un cercle.
Sur le cercle trigonométrique de rayon 1, l’abscisse de point A est donnée par :
On connaît que 


Pareil pour les ordonnées de -0.6 :
On suppose des points symétriques donc 
La longueur totale de l’arc rouge est donc la somme des deux arcs. Calculons la partie positive :

Avec l’approximation numérique de $\arccos(-0,6)$, nous avons :

Donc :
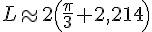
Exercice 7 – calculer une valeur approchée de la longueur L.
La figure rouge est composée d’un segment horizontal, d’un segment vertical, et d’un quart de cercle.
1. Longueur du segment vertical :
AB= 0,6
2. Longueur du segment horizontal :
3. Longueur de l’arc de cercle :
L’arc 
La position du point B sur l’arc est déterminée par :
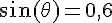

La longueur de l’arc OB est donc :
Longueur totale de L :
Valeur approchée : 2,04
Exercice 8 – algorithme et trigonométrie.
Pour 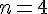
S = 0
Pour k = 0 :
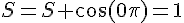
Pour k = 1 :
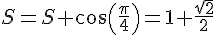
Pour k = 2 :

Pour k = 3 :
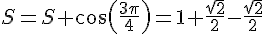
Pour k = 4 :
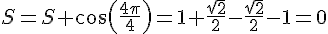
S = 0
Pour 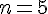
S = 0
Pour k = 0:
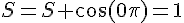
Pour k = 1:
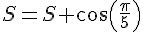
Pour k = 2:
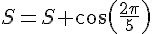
Pour k = 3:
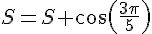
Pour k = 4:
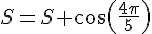
Pour k = 5:
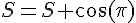
En utilisant les propriétés symétriques des fonctions trigonométriques, on trouve que toutes les cosinus s’annulent entre eux :
S = 0
Exercice 9 – mesures d’angle et point image.
a) 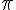
b) 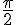
c) 
d) 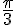
e) 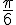
f) 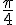
Exercice 10 – calculer la mesure d’un angle.
a) Calculer mentalement la mesure en degrés de 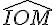
Le point M est l’image de 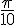
Cela correspond à un angle de 
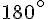
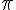
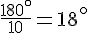
b) Donner mentalement un nombre réel dont N est le point image.
L’angle 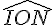
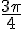
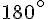
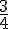
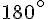
Télécharger ou imprimer cette fiche «trigonométrie : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.