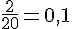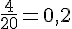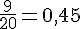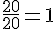Statistiques : corrigé des exercices de maths en 2de en PDF

Mis à jour le 24 novembre 2025

Les statistiques sont essentielles pour les élèves de seconde, car elles leur permettent de développer des compétences clés en maths telles que l’analyse de données, la compréhension des probabilités et l’interprétation de graphiques. Maîtriser ces concepts est crucial pour réussir dans cette matière et comprend des applications concrètes dans la vie quotidienne. Dans cet article, nous vous proposons des corrections d’exercices pour renforcer votre compréhension des statistiques.

Exercice 1 – nombre moyen de véhicules par foyer.

1. Calculer le nombre moyen de véhicules par foyer.

Pour calculer le nombre moyen de véhicules par foyer, on utilise la formule :

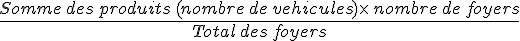
$\frac{Somme\,des\,produits\,(nombre\,de\,vehicules)\times \,nombre\,de\,foyers}{Total\,des\,foyers}$

Calcul :

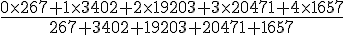
$\frac{0\times 267+1\times 3402+2\times 19203+3\times 20471+4\times 1657}{267+3402+19203+20471+1657}$

$\frac{0+3402+38406+61413+6628}{45000}$

$\frac{109849}{45000} \approx 2,44$

Donc, le nombre moyen de véhicules par foyer est d’environ 2,44.

2. Compléter les phrases suivantes :

a) « Au moins … % de foyers possèdent trois véhicules au plus » :

Somme des foyers ayant 0, 1, 2, ou 3 véhicules :

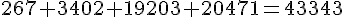
Pourcentage = 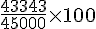$\frac{43343}{45000}\times 100$

Pourcentage = 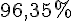$96,35\%$

b) « Au moins 50 % des foyers possèdent … véhicules ou moins » :

Somme jusqu’à 2 véhicules :

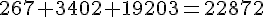
Pourcentage = $\frac{22872}{45000}\times 100$

Pourcentage = 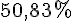$50,83\%$

Donc, au moins 50 % des foyers possèdent 2 véhicules ou moins.

Exercice 2 – documentaliste et emprunts des élèves.

a) Tableau des effectifs cumulés croissants :

0 : 39

1 : 39 + 36 = 75

2 : 75 + 23 = 98

3 : 98 + 22 = 120

4 : 120 + 20 = 140

5 : 140 + 18 = 158

6 : 158 + 10 = 168

7 : 168 + 11 = 179

8 : 179 + 5 = 184

b) Combien d’élèves ont emprunté trois livres ou plus?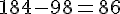

c) Calculer la fréquence cumulée croissante au millième près de la valeur 4 et l’interpréter :

Effectif total : 184

Fréquence cumulée pour 4 :

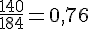
$\frac{140}{184}=0,76$

L’interprétation de 0,76 est que 76% des élèves ont emprunté au plus 4 livres.

d) Représentation de la série des effectifs par un diagramme en bâtons :

Utilisez les valeurs du premier tableau pour tracer le diagramme.

Exercice 3 – automobiliste et fréquences cumulées.

a) Fréquences cumulées croissantes en pourcentages :

Classe	[10; 15[	[15; 20[	[20; 25[	[25; 30]
Effectif cumulé	15	35	70	100
Pourcentage cumulé	15%	35%	70%	100%

b) Pourcentage des trajets durent moins de 20 min :

Le pourcentage est 35% car cela correspond aux classes [10; 15[ et [15; 20[ ( $\frac{35}{100}\times 100$ ).

c) Valeurs inférieures à 25 min :

Il y a 70 trajets de moins de 25 minutes.

d) Représentation :

– Histogramme :

Représente les effectifs de chaque classe ([10; 15[, [15; 20[, [20; 25[, [25; 30]).

– Courbe des effectifs cumulés croissants :

Trace la courbe où l’axe des abscisses porte les classes et l’axe des ordonnées les effectifs cumulés (15, 35, 70, 100).

Exercice 4 – notes du dernier devoir de mathématiques et statistiques.

a) La classe [10 ; 12[ a un effectif de 4, ce qui correspond à 5% de la classe puisque $\frac{4}{80}\times 100$ est environ 5%.

b) En additionnant les effectifs des notes inférieures à 14, on obtient 77.

Cela représente 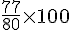$\frac{77}{80}\times 100$ soit 96,25%.

Donc la valeur exacte est supérieure à 95%.

c) Pour estimer la moyenne, on peut calculer :

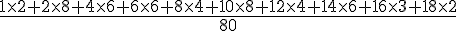
$\frac{1\times 2+2\times 8+4\times 6+6\times 6+8\times 4+10\times 8+12\times 4+14\times 6+16\times 3+18\times 2}{80}$ = 7,625.

La moyenne estimée est donc 7,625.

d) Nina a raison, la médiane est bien 8. L’effectif total est 80,

donc la médiane est la moyenne des 40ème et 41ème valeurs dans l’ordre croissant.

Les deux valeurs sont dans la classe [8 ; 10[, donc la médiane est 8.

e) Le premier quartile se trouve dans la classe [4 ; 6[ car les 20% premiers élèves (soit les 16èmes) sont dans cette classe.

Le troisième quartile se trouve dans la classe [10 ; 12[, pour les élèves autour du 60ème (75% de 80).

Exercice 5 – calcul de moyenne et de quartiles.

a) Déterminer la moyenne et la médiane :

Les notes des élèves sont : 18, 36, 44, 46, 54, 54, 55, 56, 62, 70, 73, 74, 74.

Pour calculer la moyenne :

Moyenne $= \frac{18 + 36 + 44 + 46 + 54 + 54 + 55 + 56 + 62 + 70 + 73 + 74 + 74}{13}$

$\frac{716}{13} \approx 55$

La moyenne est donc 55.

Pour déterminer la médiane :

La série ordonnée a 13 valeurs, la médiane est donc la 7ème valeur.

La médiane est : 55.

b) Déterminer les quartiles et les caractéristiques de dispersion :

Pour les quartiles :

1er quartile (Q1) : 1/4 de 13 = 3,25 donc Q1 est la 4ème valeur :

Q1 = 46.

3ème quartile (Q3) : 3/4 de 13 = 9,75 donc Q3 est la 10ème valeur :

Q3 = 70.

Pour les caractéristiques de dispersion :

L’étendue est la différence entre la valeur max et min :

Étendue = 74 – 18 = 56

L’écart interquartile est Q3 – Q1 :

Ecart interquartile = 70 – 46 = 24

Résumé des caractéristiques de dispersion :

Étendue : 56
Écart interquartile : 24

Exercice 6 – l’anaconda géant et calcul de médiane, moyenne et quartile.

Moyenne :

La moyenne se calcule en faisant la somme des tailles multipliées par leurs effectifs respectifs, divisé par le nombre total d’anacondas.

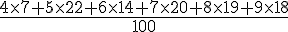
$\frac{4\times 7+5\times 22+6\times 14+7\times 20+8\times 19+9\times 18}{100}$

Calcul :

$\frac{28+110+84+140+152+162}{100}=6,94$

Médiane :

On trouve le centre de la distribution. Il y a 100 anacondas, donc la médiane est la moyenne de la 50ème et 51ème valeur.

En cumulant les effectifs : 7, 29, 43, 63… Les 50ème et 51ème valeurs sont dans la classe de taille 7 m.

Médiane = 7 m

Quartiles :

1er quartile (Q1) : 25ème valeur, donc dans la classe de taille 5 m.

1er quartile = 5 m

3ème quartile (Q3) : 75ème valeur, donc dans la classe de taille 8 m.

3ème quartile = 8 m

Caractéristiques de dispersion :

Écart interquartile : Q3 – Q1 = 8 – 5 = 3 m.

Exercice 7 – taille de requins blancs et moyenne.

Pour calculer la taille moyenne des requins, on utilise la formule de la moyenne pondérée :

$\frac{\sum(f_i \cdot x_i)}{\sum f_i}$

Avec :

f_i : l’effectif associé à chaque taille.
x_i : chaque taille de requin.

En utilisant les valeurs fournies dans le tableau :

$\frac{(1,5 \times 7) + (2 \times 10) + (2,5 \times 24) + (3 \times 32) + (3,5 \times 18) + (4 \times 4) + (4,5 \times 1)}{96}$

Effectuons les calculs :

$\frac{10,5 + 20 + 60 + 96 + 63 + 16 + 4,5}{96}$

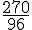
$\frac{270}{96}$

La taille moyenne des requins blancs est de : 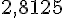mètres.

Exercice 8 – algorithme et statistiques.

1. Appliquer cet algorithme, avec chacune des listes ci-dessous.

a) Liste : 2 ; 3 ; 5 ; 25 ; 32 ; 48

– La longueur de la liste est n = 6 (pair).

– Selon l’algorithme : $i = \frac{n}{2} = \frac{6}{2} = 3$ .

– Résultat : Afficher 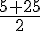$\frac{5+25}{2}$ = 15.

b) Liste : 5 ; 8 ; 16 ; 27 ; 54 ; 69 ; 84

– La longueur de la liste est n = 7 (impair).

– Selon l’algorithme : $i = \frac{n-1}{2} = \frac{7-1}{2} = 3$ .

– Résultat : Afficher 27.

2. Quel est le rôle de cet algorithme ?

Le rôle de cet algorithme est de calculer la médiane d’une liste ordonnée de nombres réels.

Si n est un nombre pair, il calcule la moyenne des deux nombres du milieu.

Si n est impair, il affiche le numéro du milieu.

Exercice 9 – fréquences cumulées et entreprise de carrelage.

a) Calcul des fréquences cumulées croissantes :

• Pour 0 carreau :
• Pour 1 carreau : $0,04 + 0,08 = 0,12$
• Pour 2 carreaux : $0,12 + 0,18 = 0,30$
• Pour 3 carreaux : $0,30 + 0,44 = 0,74$
• Pour 4 carreaux : $0,74 + 0,19 = 0,93$
• Pour 5 carreaux : $0,93 + 0,07 = 1$

b) Proportion de paquets rejetés :

L’entreprise ne peut accepter que trois carreaux défectueux au plus.

Par conséquent, la proportion de paquets rejetés est celle contenant quatre ou cinq carreaux défectueux.

• Fréquence cumulée jusqu’à 3 :
• Proportion rejetée : $1 - 0,74 = 0,26$

La proportion de paquets rejetés à intégrer dans les prévisions comptables est de 26%.

Exercice 10 – courbe des fréquences cumulées croissantes.

a) Regroupement des données :

Classes d’amplitude 5 dB à partir de 50 dB :

50 – 55
55 – 60
60 – 65
65 – 70
70 – 75

b) Histogramme :

Pour réaliser un histogramme, compter le nombre de données dans chaque classe :

50 – 55 : 2 données
55 – 60 : 2 données
60 – 65 : 5 données
65 – 70 : 6 données
70 – 75 : 5 données

c) Fréquences cumulées croissantes :

50 – 55 : $\frac{2}{20}=0,1$
55 – 60 : $\frac{4}{20}=0,2$
60 – 65 : $\frac{9}{20}=0,45$
65 – 70 : $\frac{15}{20}=0,75$
70 – 75 : $\frac{20}{20}=1$

d) Classe de plus grande fréquence :

La classe 65 – 70 dB est la plus fréquente avec 6 véhicules mesurés dans cette intervalle.

Cela indique que la plupart des véhicules avaient un niveau sonore dans cette plage.

4.8/5 - (32784 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «statistiques : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Vecteurs

Résolution graphique d’équations et inéquations

Intervalles et valeur absolue

Les équations de droites

Systèmes de deux équations à deux inconnues

Algorithmes et programmes

Simulation et échantillonnage

Trigonométrie

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 357 917 cours et exercices de maths téléchargés en PDF et 4 250 exercices.