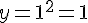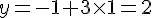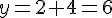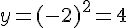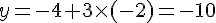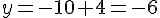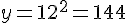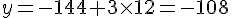Algorithmes et programmes : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Dans cet article dédié aux corrections d’exercices de mathématiques en seconde, nous allons explorer les algorithmes et les programmes, des concepts essentiels pour développer des compétences en raisonnement logique et en résolution de problèmes. Comprendre ces notions permet aux élèves de mieux appréhender les systèmes informatiques et d’appliquer leurs connaissances mathématiques de manière pratique. Ce travail est crucial pour renforcer la confiance des élèves et les préparer à des études futures en sciences et technologies.
Exercice 1 – programme avec le langage Python.
a) Le type de la variable x est entier (int) car elle est convertie par la fonction int().
b) Pour chaque valeur de x :
• Si x = 3 :
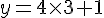
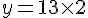
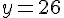
• Si x = -1 :
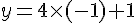
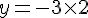
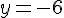
• Si x = 11 :
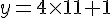
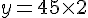
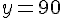
c) La fonction définie est 
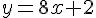
Exercice 2 – décrire le rôle et fonctionnement de l’algorithme.
L’algorithme a pour fonction de calculer la longueur d’une chaîne de caractères donnée, puis d’extraire et d’afficher le premier caractère de cette chaîne.
Voici le fonctionnement de l’algorithme pas à pas :
1. Entrée : L’utilisateur saisit une chaîne de caractères non vide, notée C.
2. Traitement :
-
- Assigner à \ell la valeur Lgr(C), qui représente le nombre de caractères de la chaîne C.
- Assigner à C’ la sous-chaîne Sch(C,
,
).
Cela signifie que l’on extrait à partir de la position 1, une sous-chaîne de longueur 1.
3. Sortie : Afficher C’, qui est le premier caractère de la chaîne initiale C.
Exercice 3 – programme et magasin de reprographie.
a) Compléter les lignes ① et ② :
Complétez le programme comme suit :
print("Entrer N :")
N=int(input())
if N \leq 50:
\qquad Prix=N \times 0.15
else:
\qquad Prix=N \times 0.10
print("Prix=", Prix)
b) Saisir le programme à l’ordinateur :
Il est important de saisir correctement le programme pour obtenir le résultat souhaité.
c) Contrôler son fonctionnement à l’aide d’exemples :
Vérifions la calculatrice avec quelques exemples :
Pour N = 30 photocopies :
Prix = 
Pour N = 60 photocopies :
Prix = 60 \times 0.10 = 6€
Exercice 4 – algorithme qui affiche la distance.
a) Calcul du temps mis par Louise :
Pour les 5 premiers kilomètres, elle court à 15 km/h :
Le temps pour 5 km est : 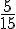
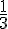
Pour les 2 km restants, elle court à 12 km/h :
Le temps pour 2 km est : 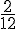
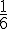
Le temps total est : 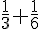
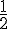
b) Algorithme :
L’algorithme suivant calcule et affiche la distance parcourue 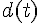

Entrée : Un temps 
Traitement :
Convertir le temps en heures : 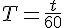
Si 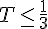
Calculer 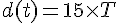
Sinon :
Calculer 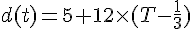
Sortie : Afficher 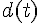
Exercice 5 – un algorithme à étudier.
a) Exécuter cet algorithme avec la valeur n = 5 en entrée.
Pour 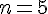
– Pour
– Pour
– Pour
– Pour
– Pour
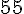
b) De façon plus générale, expliquer le rôle de cet algorithme.
Le rôle de cet algorithme est de calculer la somme des carrés des entiers naturels de 1 à 
Formellement, il calcule la valeur de la somme :
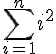
Exercice 6 – un algorithme qui donne l’image par une fonction.
Pour écrire un algorithme qui donne l’image par une fonction selon 
Algorithm f(x)
Input: x
Output: f(x)
If x  0 Then
f(x) := x2
ElseIf 0 < x
0 Then
f(x) := x2
ElseIf 0 < x  1 Then
f(x) := x
Else
f(x) := -2x + 3
EndIf
Return f(x)
EndAlgorithm
1 Then
f(x) := x
Else
f(x) := -2x + 3
EndIf
Return f(x)
EndAlgorithm
Exercice 7 – simuler 100 lancers avec Python.
a) Rôle des variables :
- n: Cette variable compte le nombre de lancés qui donnent « Pile ».
- i: C’est l’indice de la boucle, allant de 1 à 100 pour réaliser les 100 lancers.
- x: Cette variable reçoit un nombre aléatoire compris entre 0 et 1 à chaque lancer.
b) Modification pour M simulations :
Pour que Suzy puisse effectuer M fois la simulation, elle doit ajouter une boucle extérieure qui exécute la simulation complète M fois. Voici une suggestion de modification :
from random import random
for simulation in range(M): # Effectuer M simulations
n=0
for i in range(1,101):
x=random()
if x<0.5:
n=n+1
print("n=",n)
Explication : La boucle extérieure for simulation in range(M): permet de répéter le processus des 100 lancers de pièce M fois, et le compteur n est réinitialisé à zéro pour chaque simulation.
Exercice 8 – donner un programme qui fournit les 100 premiers entiers.
a) Réponse : La fonction diviseurs(N) calcule le nombre de diviseurs de N. Elle initialise une variable x à 0, puis parcourt tous les entiers k de 1 à N. Si k divise N, elle incrémente x de 1. Finalement, elle renvoie x. Donc, elle retourne le nombre de diviseurs de N.
b) Programme en pseudo-code :
Pour chaque entier N de 1 à 100 :
- Initialiser x à 0.
- Pour k allant de 1 à N :
- Si k divise N alors ajouter 1 à x.
- Si x est au moins 10, afficher N.
Exercice 9 – un programme écrit en Python.
a) Le type de la variable x est entier (int).
b)
Pour chaque valeur de x :
– Si x = 1 :
- Calcul de y :
– Si x = -2 :
- Calcul de y :
– Si x = 12 :
- Calcul de y :
c) La fonction définie par le programme est 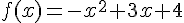
Exercice 10 – un programme écrit avec le langage Python.
a) Réponse :
Lorsque l’on saisit 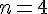
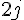
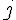

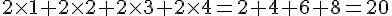
La valeur affichée est donc 20.
b) Explication générale :
De façon générale, le programme calcule la somme des termes de la forme 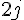
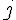

Cela correspond à la somme :
Ce qui peut être simplifié par le facteur commun :
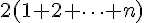
La somme des entiers de 1 à 
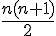
Donc, le programme calcule :
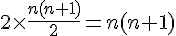
Télécharger ou imprimer cette fiche «algorithmes et programmes : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.


 ,
, 




 0 Then
f(x) := x2
ElseIf 0 < x
0 Then
f(x) := x2
ElseIf 0 < x