Fonction carrée et polynôme : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Exercice 1 – fonction polynôme et parabole.
a) Maximum ou minimum : La fonction g est un polynôme de degré 2 de la forme 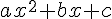
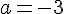
Comme 
b) Tabulation de g :
c) Sommet de la parabole :
L’abscisse 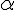
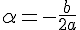
Donc, 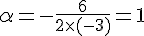
L’ordonnée 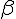
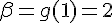
Le sommet S est donc 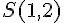
d) Tracé de la parabole :
Pour tracer la parabole, utilisez les points de la tabulation ainsi que le sommet 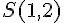
La parabole passe par ces points et a son maximum au sommet.
Exercice 2 – fonction polynôme de degré 2.
a) Pour afficher la parabole P à l’écran de la calculatrice, entrez l’équation 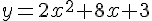
La parabole est une courbe symétrique par rapport à son sommet.
Le sommet S d’une parabole de la forme 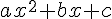
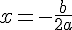
Pour notre équation, 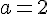
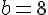
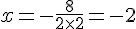
On remplace 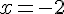
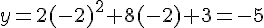
Ainsi, le sommet S est 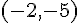
b) L’équation entrée dans l’écran de calcul indique que la résolution 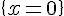
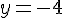
e qui n’est pas pertinent ici pour la conjecture du sommet, qui est à 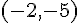
c) Pour tracer la parabole P, utilisez la carte graphique de la calculatrice pour visualiser
l’équation 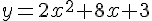
Exercice 3 – tableau et étude du signe d’un produit.
a) Étude du signe de 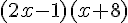

Les racines de l’expression sont obtenues en résolvant :
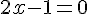
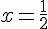
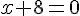
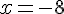
Ces racines divisent la droite réelle en intervalles :
Tableau de signes :
| x | 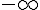
|
-8 | 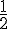
|

|
|---|---|---|---|---|
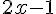
|
– | – | 0 | + |
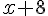
|
– | 0 | + | + |
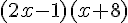
|
+ | 0 | – | + |
b) Résolution de l’inéquation : 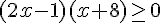
La solution est : 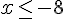
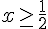
c) Contrôle graphique :
Pour vérifier graphiquement, tracer la courbe de la fonction 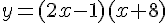
et observer les intervalles où la courbe est au-dessus ou sur l’axe des abscisses.
Exercice 4 – résoudre une inéquation et étude de signe du produit.
a) Étudier le signe de (4+x)(2+x).
Nous allons utiliser un tableau de signes pour déterminer les intervalles où le produit est positif, négatif ou nul.
- Les zéros des facteurs sont x = -4 et x = -2.
- On divise donc la droite des réels en trois intervalles :
, ]-4, -2[ , et
.
Construisons le tableau de signes :
| x | [-∞, -4[ | -4 | ]-4, -2[ | -2 | ]-2, +∞[ |
|---|---|---|---|---|---|
| 4+x | – | 0 | + | + | + |
| 2+x | – | – | – | 0 | + |
| (4+x)(2+x) | + | 0 | – | 0 | + |
b) Résoudre l’inéquation (4+x)(2+x) < 0.
L’inéquation est négative sur l’intervalle 
Solution :
Exercice 5 – résoudre graphiquement des inéquations.
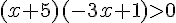
Pour cette inéquation, déterminons d’abord les zéros des facteurs :
Cherchons les intervalles de signe avec un tableau de signes :
| Intervalle | x+5 | -3x+1 | Produit |
|---|---|---|---|
![]-\infty, -5[](https://maths-pdf.fr/latex-images/11a7fecc1c84e7ea873348f52f746ca2.png) |
– | + | – |
![]-5, \frac{1}{3}[](https://maths-pdf.fr/latex-images/719288c33d97864b529c5ca5dc8c4ea2.png) |
+ | + | + |
 |
+ | – | – |
Solution :
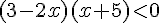
Tableau de signes :
| Intervalle | 3-2x | x+5 | Produit |
|---|---|---|---|
![]-\infty, -5[](https://maths-pdf.fr/latex-images/11a7fecc1c84e7ea873348f52f746ca2.png) |
+ | – | – |
 |
+ | + | + |
 |
– | + | – |
Solution : ![x \in ]-5, \frac{3}{2}[](https://maths-pdf.fr/latex-images/71a25ad530bc230a5f52f5e2474f9f7b.png)
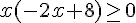
Tableau de signes :
| Intervalle | x | -2x+8 | Produit |
|---|---|---|---|
![]-\infty, 0[](https://maths-pdf.fr/latex-images/7f0ec415fa3d43de1aa4c34decdbb0a0.png) |
– | + | – |
![[0, 4]](https://maths-pdf.fr/latex-images/045d5c243903d167f321bbc4e710606a.png) |
+ | + | + |
 |
+ | – | – |
Solution :
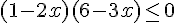
Tableau de signes :
| Intervalle | 1-2x | 6-3x | Produit |
|---|---|---|---|
![]-\infty, \frac{1}{2}[](https://maths-pdf.fr/latex-images/02731e19a0710a2935485ee3028d147c.png) |
+ | + | + |
![[\frac{1}{2}, 2]](https://maths-pdf.fr/latex-images/e9fcfaed7c27b69d06afadfbd4581a4f.png) |
+ | – | – |
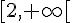
|
– | – | + |
Solution :
Exercice 6 – aire d’un rectangle et fonctions.
a) Placer le point M :
Pour que l’aire du triangle AMN soit comprise entre le quart et la moitié de l’aire du rectangle ABCD :
L’aire du rectangle ABCD est 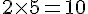
Donc,
aire minimum = 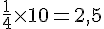
aire maximum = 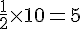
L’aire du triangle AMN est :
Étant donné que 
On résout :
Donc
Cela signifie
b) Sur l’affirmation de Xavier :
L’aire maximale de AMN est 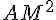
Puisque 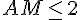
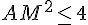
Les trois quarts de l’aire du rectangle ABCD est :
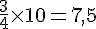
Donc, Xavier a raison, car l’aire maximale possible pour AMN est 4 cm2, qui est inférieure à 7,5 cm2.
Exercice 7 – aire d’un triangle et fonctions.
Étape 1 : Calcul de l’aire du triangle ABC.
Le triangle ABC est rectangle en A, donc son aire est donnée par :
Étape 2 : Aire du triangle BMN.
L’aire requise est au moins le quart de celle de ABC :
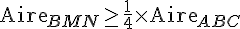
Étape 3 : Positionnement de M.
BMN est rectangle en M, donc :
Le théorème de Pythagore dans BMN nous donne :
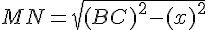
En remplaçant BC par la valeur de l’hypoténuse AC :
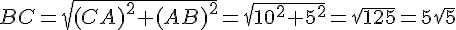
Il faut satisfaire :
Il s’agit de résoudre cette inéquation pour trouver la valeur minimale de x.
Exercice 8 – programme de calcul et fonctions.
a) On choisit le nombre 5,5. Suivons le programme de calcul étape par étape :
– Ajouter 7 : 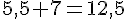
– Élever au carré : 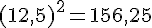
– Multiplier par 2 : 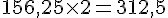
– Soustraire 8 : 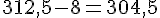
Résultat : 304.5
b) Soit 
– Ajouter 7 : 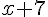
– Élever au carré : 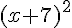
– Multiplier par 2 : 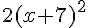
– Soustraire 8 : 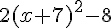
Expression finale : 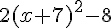
c) Pour que le nombre obtenu soit minimal, il suffit de minimiser l’expression. Comme 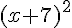
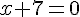
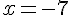
Vérification :
Pour 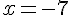
– Ajouter 7 : 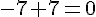
– Élever au carré : 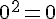
– Multiplier par 2 : 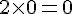
– Soustraire 8 : 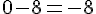
Nombre minimal : -8
Exercice 9 – logiciel de calcul formel et fonctions.
a) Rédiger un programme de calcul associé à cette fonction 
La fonction est donnée sous la forme canonique : 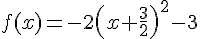
b) Quel nombre obtient-on lorsqu’on choisit :
Le nombre 0 ? :
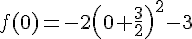
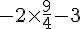
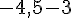
Le nombre -1,5 ? :
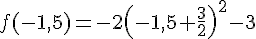
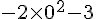
c) Peut-on choisir un nombre de façon que le nombre obtenu avec ce programme de calcul soit maximal ?
La fonction quadratique sous forme canonique atteint son maximum quand 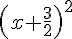
c’est-à-dire quand 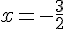
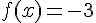
Exercice 10 – algorithme et calculatrice.
1. a) Algorithme :
Saisir une valeur de 
Calculer 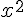

Si 
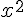
Sinon, afficher 
1. b) Test de l’algorithme :
Testez pour quelques valeurs de 
On peut conjecturer que la valeur minimale des deux est 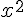



2. a) Courbes :
Utilisez une calculatrice pour tracer les courbes 

2. b) Confirmation de la conjecture :
Oui, la courbe confirme que pour 



3. Démonstration algébrique :
Comparer 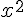

On veut résoudre 
Reformulons l’inéquation : 
Donc, 
Pour 
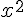


Télécharger ou imprimer cette fiche «fonction carrée et polynôme : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.

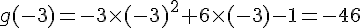
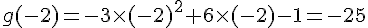
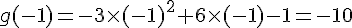
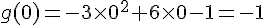
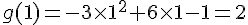
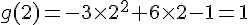
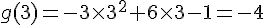
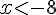
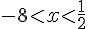
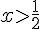
![x\in -]\infty, -4]](https://maths-pdf.fr/latex-images/7ea842cc941efcf5c10db84d6685e059.png) , ]-4, -2[ , et
, ]-4, -2[ , et ![]-2, +\infty[](https://maths-pdf.fr/latex-images/9df6b155df131900fd566ae173688cf2.png) .
.


![x \in ]-5, \frac{1}{3}[](https://maths-pdf.fr/latex-images/ede4cf6dec90391dc1070c616e2dd4a5.png)

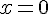

![x \in [0, 4]](https://maths-pdf.fr/latex-images/c881fdd790214d5784872f40e56d3563.png)


![x \in [\frac{1}{2}, 2]](https://maths-pdf.fr/latex-images/5484642eb460f20aaa63be5085d56400.png)















