Géométrie dans l’espace : corrigé des exercices de maths en 2de en PDF

Mis à jour le 24 novembre 2025

La géométrie dans l’espace est une composante essentielle du programme de mathématiques en seconde, permettant aux élèves de développer des compétences clés en visualisation, raisonnement spatial et calcul. Maîtriser les concepts de la géométrie dans l’espace aide non seulement à exceller dans les examens, mais aussi à renforcer des bases solides pour des études futures en maths et dans des domaines connexes. À travers les corrections d’exercices pratiques, les élèves apprendront à appliquer efficacement leurs connaissances et à résoudre des problèmes complexes.

Exercice 1 – volume d’un pavé droit.

1. Calcul de la hauteur du pavé :

Le volume d’un pavé se calcule avec la formule : $V=L\times \ell\times h$

On connaît : 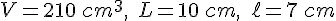$V=210\,cm^3,\;L=10\,cm,\;\ell=7\,cm$

En remplaçant, on a : $210=10\times 7\times h$

Donc :

2. Volume d’un cube lorsque sa longueur d’arête est triplée :

Volume initial du cube : 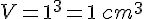$V=1^3=1\,cm^3$

Longueur de l’arête triplée : 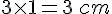$3\times 1=3\,cm$

Nouveau volume : $V=3^3=27\,cm^3$

3. Utilisation du cube pour citer des droites :

Parallèles : Les droites (AB) et (EF)

Sécantes : Les droites (AB) et (BC)

Non coplanaires : Les droites (AB) et (EH)

Exercice 2 – représentations en perspective cavalière.

1) Cube d’arêtes de longueur 6 carreaux :

Pour dessiner le cube, chaque arête doit mesurer 6 carreaux tout en respectant l’angle de fuite.

Tracez six carreaux dans chaque direction à partir d’un sommet.

2) Cube d’arêtes de longueur 5 carreaux :

Chaque arête mesure 5 carreaux.

Prolongez chaque angle et côté du cube initial de sorte que chacun mesure 5 carreaux.

3) Parallélépipède rectangle de dimensions 3, 5, et 6 carreaux :

Dessinez une face de base 3 carreaux de largeur et 5 carreaux de hauteur.

Puis, prolonger la profondeur de 6 carreaux en respectant l’angle de fuite.

4) Pyramide de hauteur 6 carreaux à base carré de côté 3 carreaux :

Commencez par dessiner une base carrée de 3 carreaux de côté.

Le sommet de la pyramide se situe sur un axe de symétrie de la base, à 6 carreaux au-dessus du centre de la base.

Exercice 3 – construire le patron d’un cube.

Pour construire le patron du cube, il faut déplier les faces en veillant à placer correctement les motifs.

Voici une suggestion de patron :

Face du haut (visible) : motif A
Face avant (visible) : motif \nabla
Face droite (visible) : motif \partial
Face gauche (non visible) : motif \infty
Face arrière (non visible) : motif \emptyset
Face du bas (non visible) : motif \mathcal{H}

Ce patron peut être représenté en forme de croix, chaque face adaptée selon sa position et ses motifs visibles ou non visibles.

Exercice 4 – construire le patron d’un prisme.

Pour construire le patron du prisme ABCDEFGH, suivez les étapes ci-dessous :

Commencez par dessiner le carré EFGH avec un côté de 2 cm.
À partir du point E, tracez le segment ED perpendiculaire à EH mesurant 5 cm.
Tracez le segment DC parallèle à HG mesurant 2 cm.
Complétez le carré DCGH en traçant les segments CG et DH, chacun mesurant 2 cm.
Pour former le trapèze rectangle ADHE, tracez le segment AD parallèle à EH mesurant 5 cm.
Reliez les points A et E pour compléter le trapèze rectangle ADHE.
Répétez le même processus à partir de B pour former le trapèze rectangle BCGF, mesurant aussi 5 cm pour BC et FG.

Le patron complet doit ressembler à une croix avec deux carrés (EFGH et DCGH) et quatre trapèzes rectangles (ADHE, BCGF de chaque côté des carrés).

Exercice 5 – représenter un tétraèdre en perspective cavalière.

1) Représentation du tétraèdre :

Tracez un triangle équilatéral pour ABC et placez S au-dessus du centre de ce triangle.

2) Calcul de la longueur IS :

Dans le triangle équilatéral ABC de côté 4 cm, I est le milieu de [AB]. Donc, AI = \frac{4}{2} = 2 cm.

Pour calculer IS, utilisons Pythagore dans le triangle ABS :

$AS=\sqrt{4^2-2^2}$

Donc, $IS = 2\sqrt{3}$ cm.

3) Calcul de la longueur SH :

SH est la hauteur du tétraèdre. Nous savons que SH est l’axe du cercle qui est inscrit dans le triangle équilatéral ABC.

La formule pour la hauteur d’un tétraèdre régulier de côté a est :

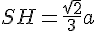
$SH=\frac{\sqrt{2}}{3}a$

Donc, 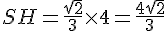$SH=\frac{\sqrt{2}}{3}\times 4=\frac{4\sqrt{2}}{3}$

4) Calcul du volume de ABCS :

Le volume V d’un tétraèdre régulier de côté a est donné par :

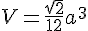
$V=\frac{\sqrt{2}}{12}a^3$

En remplaçant a par 4 cm :

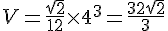
$V=\frac{\sqrt{2}}{12}\times 4^3=\frac{32\sqrt{2}}{3}$

Exercice 6 – un patron pour confectionner une initiale.

Pour concevoir le patron de cette lettre « H », nous devons prendre en compte toutes les dimensions visibles du modèle et représenter chaque face à plat :

1. Face avant et arrière (2 rectangles) :

Chaque mesure 6 cm de hauteur et 6 cm de largeur.

2. Faces latérales (4 rectangles) :

Chaque mesure 6 cm de hauteur et 2 cm de largeur.

3. Faces supérieures et inférieures (3 rectangles) :

Les deux sections verticales mesurent chacune 1 cm de largeur et 6 cm de longueur, tandis que la section horizontale au milieu mesure 1 cm de largeur et 4 cm de longueur.

Pour construire le patron :

Tracez deux grands rectangles de 6 cm x 6 cm pour les faces avant et arrière.
Ajoutez quatre petits rectangles de 6 cm x 2 cm pour les côtés latéraux.
Ajoutez trois rectangles de 1 cm x 6 cm pour les sections verticales supérieures/inférieures et un rectangle de 1 cm x 4 cm pour la section horizontale centrale.

Illustration : À l’aide d’un patron en papier ou en carton léger, connectez les rectangles selon les dimensions indiquées pour former la lettre « H » tridimensionnelle.

Exercice 7 – volume du chocolat pour une boule pleine.

Chaque boule de chocolat a la forme d’une sphère complète.

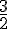
Le diamètre est de 3 cm, donc le rayon est de $\frac{3}{2}$

Le volume d’une sphère est donné par la formule :

$V=\frac{4}{3}\pi r^3$

En substituant 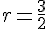$r=\frac{3}{2}$

$V=\frac{4}{3}\pi(\frac{3}{2})^3$

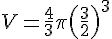
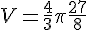
$V=\frac{4}{3}\pi\frac{27}{8}$

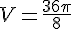
$V=\frac{36\pi}{8}$

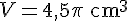
$V=4,5\pi\,\text{cm}^3$

Pour 24 boules, le volume total est :

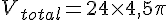
$V_{total}=24\times 4,5\pi$

$V_{total}=108\pi\,cm ^3$

Donc, le volume total de chocolat nécessaire est de 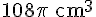$108\pi\,\text{cm}^3$

Exercice 8 – volume de la part d’un camembert.

Pour résoudre cet exercice, nous devons d’abord calculer le volume total du camembert en forme de cylindre.

La formule du volume d’un cylindre est : $V=\pi\times r^2\times h$

Où :

est le rayon du cylindre, soit $5,5\ cm$ (car le diamètre est 11 cm).
est la hauteur du cylindre, soit $3\ cm$ .

Donc, le volume total du camembert est :

$V=\pi\times (5,5)^2\times 3$

$V\approx285,36\ cm^3$

La part découpée représente 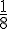$\frac{1}{8}$

Le volume de la part est donc :

$V_{part}=\frac{1}{8}\times 285,36$

$V_{part}\approx35,67\ cm^3$

Le volume de la part est environ $35,67\ cm^3$

Exercice 9 – réduction de la pyramide de Khéops.

1) Représentation en perspective cavalière :

Pour représenter la pyramide en perspective cavalière, nous choisissons un coefficient de réduction de 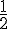$\frac{1}{2}$ .

Cela signifie que les dimensions sont réduites de moitié.

2) Calcul du volume initial :

Le volume d’une pyramide est donné par la formule :

$V=\frac{1}{3}\times base\times hauteur$

La base est un carré de côté 230,3 m, donc :

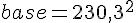
La hauteur initiale était de 146,6 m.

Donc le volume initial est :

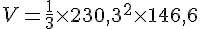
$V=\frac{1}{3}\times 230,3^2\times 146,6$

Calculons :

$V\approx2,592\times 10^6\ m^3$

3) Volume actuel et perte de volume :

La hauteur actuelle est de 138,7 m :

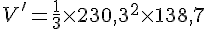
$V'=\frac{1}{3}\times 230,3^2\times 138,7$

Calculons :

$V'\approx2,521\times 10^6\ m^3$

La perte de volume est :

$\Delta V=2,592\times 10^6-2,521\times 10^6$

$\Delta V\approx71\times 10^3\ m^3$

Exercice 10 – droites parallèles et coplanaires dans un parallélépipède.

1) Les droites 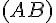et définissent un plan. Ce plan est (ABHG).

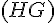
2) Les droites 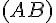et définissent un plan. Ce plan est (ABCG).

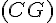
3) Trois droites parallèles à 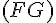sont : , et .

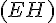
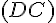
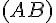
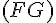
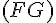
4) Trois droites sécantes à sont : , et .

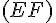
5) Trois droites non coplanaires à 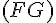sont : , et .

4.9/5 - (33498 votes)

Télécharger puis imprimer cette fiche en PDF.

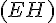
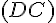
Télécharger ou imprimer cette fiche «géométrie dans l'espace : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Statistiques

Trigonométrie

Systèmes de deux équations à deux inconnues

Fonction carrée et polynôme

Algorithmes et programmes

Simulation et échantillonnage

Les équations et inéquations

Intervalles et valeur absolue

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 357 917 cours et exercices de maths téléchargés en PDF et 4 250 exercices.