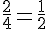Probabilités : corrigé des exercices de maths en 2de en PDF

Mis à jour le 24 novembre 2025

Les probabilités représentent une notion essentielle du programme de mathématiques en seconde, permettant aux élèves de développer des compétences analytiques cruciales. En maîtrisant les calculs de probabilités et l’analyse de situations aléatoires, les lycéens acquièrent une compréhension approfondie des statistiques et du raisonnement logique. La pratique régulière à travers des exercices corrigés favorise l’autonomie et la confiance en mathématiques, des atouts indispensables pour leur avenir académique.

Exercice 1 – une pièce équilibrée et arbre de probabilité.

a) Reproduire et compléter l’arbre des possibles :

En lançant la pièce deux fois, nous obtenons les résultats suivants :

Premier lancer : 1 ou 2
Deuxième lancer : 1 ou 2

Les sommes possibles sont :

1 + 1 = 2
1 + 2 = 3
2 + 1 = 3
2 + 2 = 4

b) Déterminer la probabilité associée à chaque issue :

Il y a 4 issues possibles : (1,1), (1,2), (2,1), (2,2).

La probabilité de chaque couple est : 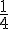$\frac{1}{4}$

Probabilités pour chaque somme :

Somme 2 : (1,1) $\Rightarrow$ $\frac{1}{4}$
Somme 3 : (1,2) et (2,1) $\Rightarrow$ $\frac{2}{4}=\frac{1}{2}$
Somme 4 : (2,2) $\Rightarrow$ $\frac{1}{4}$

Exercice 2 – une boule dans un sac et issues possibles.

a) Félix affirme qu’il y a une chance sur deux de tirer une boule bleue. Or, dans le sac, il y a au total 6 boules : 3 vertes, 2 bleues, et 1 rouge.

Donc, la probabilité de tirer une boule bleue est :

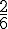
$\frac{2}{6}$

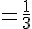
$=\frac{1}{3}$

Félix se trompe, la probabilité est 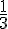$\frac{1}{3}$

b) Issues possibles et probabilités :

- Tirer une boule rouge : 1 rouge sur 6 boules au total

Probabilité = 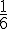$\frac{1}{6}$

- Tirer une boule bleue : 2 bleues sur 6 boules au total

Probabilité = 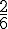$\frac{2}{6}$

Probabilité réduite = 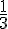$\frac{1}{3}$

- Tirer une boule verte : 3 vertes sur 6 boules au total

Probabilité = 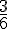$\frac{3}{6}$

Probabilité réduite = 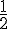$\frac{1}{2}$

Exercice 3 – déterminer la probabilité d’un événement.

a) Peut-on utiliser le modèle d’équiprobabilité ?

Oui, car chaque carte a la même probabilité d’être tirée dans un jeu complet de 32 cartes.

b) Déterminer la probabilité de l’événement :

A : « La carte tirée est une Dame » :

Il y a 4 Dames dans un jeu de 32 cartes. La probabilité est donc :

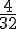
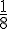
$\frac{4}{32}$ = $\frac{1}{8}$

B : « La carte tirée est un Cœur » :

Il y a 8 Cœurs dans un jeu de 32 cartes (puisqu’il y a 4 couleurs et 32 cartes au total, donc 32 ÷ 4 = 8). La probabilité est donc :

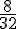
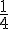
$\frac{8}{32}$ = $\frac{1}{4}$

Exercice 4 – jeu de grattage et probabilité.

Événement A : « On gagne au moins 20 € »

Pour cet événement, on additionne les probabilités des gains de 20 € et 1000 € :

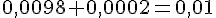
Événement B : « On gagne 5 € au plus »

Pour cet événement, on additionne les probabilités des gains de 0 €, 1 € et 5 € :

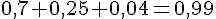
Exercice 5 – une urne et détermination de la probabilité d’un événement.

Événement A : « La lettre tirée n’est pas une voyelle ».

Il y a 5 voyelles dans l’alphabet : A, E, I, O, U.

Donc, il y a 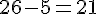consonnes.

La probabilité que la lettre tirée ne soit pas une voyelle est :

Réponse A : 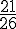$\frac{21}{26}$

Événement B : « La lettre tirée est avant M dans l’ordre alphabétique ».

Les lettres avant M sont : A, B, C, D, E, F, G, H, I, J, K, L.

Il y a donc 12 lettres avant M.

La probabilité que la lettre tirée soit avant M est :

Réponse B : 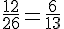$\frac{12}{26}=\frac{6}{13}$

Exercice 6 – tirage d’une carte au hasard.

1. Probabilité de tirer le 5 de Carreau :

a) Pour Hugo : Il y a 32 cartes dans le jeu et seulement un 5 de Carreau.

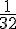
$\frac{1}{32}$

b) Pour Chloé : Il y a 52 cartes dans le jeu et seulement un 5 de Carreau.

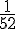
$\frac{1}{52}$

2. Inès affirme que la probabilité de tirer un Cœur est la même pour Hugo et Chloé :

Pour Hugo : Il y a 8 Cœurs dans un jeu de 32 cartes.

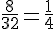
$\frac{8}{32}=\frac{1}{4}$

Pour Chloé : Il y a 13 Cœurs dans un jeu de 52 cartes.

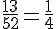
$\frac{13}{52}=\frac{1}{4}$

Donc, elle a raison. Les probabilités sont égales.

3. Tirage d’un As :

Pour Hugo : Il y a 4 As dans un jeu de 32 cartes.

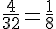
$\frac{4}{32}=\frac{1}{8}$

Pour Chloé : Il y a 4 As dans un jeu de 52 cartes.

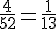
$\frac{4}{52}=\frac{1}{13}$

Hugo a une plus grande probabilité de tirer un As.

Exercice 7 – déterminer la probabilité de l’union.

a) Traduction de l’événement R ∪ H :

L’événement R ∪ H signifie que l’élève choisi joue soit au rugby, soit au handball, ou aux deux.

b) Détermination de la probabilité de R ∪ H :

La probabilité de l’union de deux événements est donnée par la formule :

$P(R\cup H)=P(R)+P(H)-P(R\cap H)$

En utilisant les valeurs données :

$P(R\cup H)=0,56+0,37-0,29$

En calculant, nous trouvons :

$P(R\cup H)=0,64$

Donc, la probabilité que l’élève choisi joue soit au rugby, soit au handball, ou aux deux, est 0,64.

Exercice 8 – la probabilité d’une population et le caractère génétique.

a) Déterminer la probabilité qu’il possède au moins l’un des deux caractères.

On utilise la formule de probabilité de l’union de deux événements :

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Avec P(A) = 0,8, P(B) = 0,6 et P(A \cap B) = 0,45.

Donc : $P(A\cup B)=0,8+0,6-0,45=0,95$

La probabilité qu’il possède au moins l’un des deux caractères est donc de 0,95.

b) Déterminer la probabilité qu’il possède ni le caractère A ni le caractère B.

La probabilité qu’il ne possède ni le caractère A ni le caractère B est le complément de la probabilité qu’il possède au moins l’un des deux caractères :

$P(\overline{A\cup B})=1-P(A\cup B)$

Donc : $P(\overline{A\cup B})=1-0,95=0,05$

La probabilité qu’il ne possède ni le caractère A ni le caractère B est donc de 0,05.

Exercice 9 – déterminer la probabilité de chaque événement.

a) 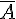$\overline{A}$

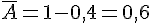
$\overline{A}=1-0,4=0,6$

b)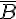 $\overline{B}$

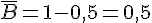
$\overline{B}=1-0,5=0,5$

c) $\overline{A \cap B}$

Formule : $P(A \cup B) = P(A) + P(B) - P(A \cap B)$

$P(A\cap B)=0,4+0,5-0,6=0,3$

d) $\overline{A} \cap B$

Formule : $\overline{A} \cap B = B - (A \cap B)$

$P(\overline{A}\cap B)=0,5-0,3=0,2$

e) $A \cap \overline{B}$

$P(A\cap \overline{B})=0,4-0,3=0,1$

f) $\overline{A} \cap \overline{B}$

$P(\overline{A}\cap \overline{B})=1-0,6=0,4$

Exercice 10 – une école de commerce avec probabilités et fréquences.

a) 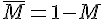$\overline{M}=1-M$

a) Probabilité que l’étudiant ne soit pas inscrit en Marketing :

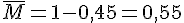
$\overline{M}=1-0,45=0,55$

b) Probabilité que l’étudiant ne soit pas inscrit en Négociation :

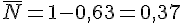
$\overline{N}=1-0,63=0,37$

c) Probabilité que l’étudiant soit inscrit uniquement en Marketing :

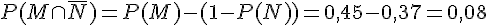
$P(M\cap\overline{N})=P(M)-(1-P(N))=0,45-0,37=0,08$

d) Probabilité que l’étudiant soit inscrit dans au moins une des deux options :

$P(M\cup N)=1-0,18=0,82$

e) Probabilité que l’étudiant soit inscrit en Marketing ou en Négociation ou les deux :

$P(M\cup N)=0,82$

f) Probabilité que l’étudiant soit inscrit aux deux options :

$P(M\cap N)=P(M)+P(N)-P(M\cup N)=0,45+0,63-0,82=0,26$

4.8/5 - (30624 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «probabilités : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Fonction carrée et polynôme

Vecteurs

L’étude de fonction

Statistiques

Résolution graphique d’équations et inéquations

Simulation et échantillonnage

Fonction inverse

Géométrie dans l’espace

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 357 911 cours et exercices de maths téléchargés en PDF et 4 250 exercices.