Vecteurs : corrigé des exercices de maths en 2de en PDF

Mis à jour le 24 novembre 2025

Les vecteurs représentent un enjeu clé dans le programme de mathématiques de seconde, permettant aux élèves de développer des compétences essentielles telles que la représentation graphique, les calculs algébriques et la résolution de problèmes. Comprendre les vecteurs est crucial pour aborder des notions plus avancées en géométrie et en physique. Ce guide de corrections d’exercices est conçu pour aider les élèves à maîtriser ces concepts fondamentaux et améliorer leurs performances scolaires.

Exercice 1 – démontrer qu’un quadrilatère est un parallélogramme.

a) Construction du point D :

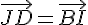
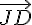
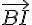
Pour construire le point D tel que $\vec{JD}=\vec{BI}$ , il faut que le vecteur $\vec{JD}$ soit égal au vecteur $\vec{BI}$ .

Pour y parvenir, suivez ces étapes :

– Placez le point initial I sur le segment [AB].

– Depuis J, tracez un vecteur égal à 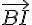$\vec{BI}$ , ce qui fixe la position de D.

b) Montrer que le quadrilatère BIEF est un parallélogramme :

Les points E et F sont définis comme les symétriques des points J et D par rapport au point C.

On va démontrer que BIEF est un parallélogramme.

1. Propriété des symétriques :

Le symétrique d’un point par rapport à un autre est tel que ce dernier est le milieu du segment formé par le point et son symétrique.

Cela implique :

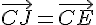
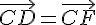
$\vec{CJ}=\vec{CE}$ et $\vec{CD}=\vec{CF}$

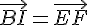
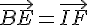
2. Parallélisme : Montrons que $\vec{BI}=\vec{EF}$ et $\vec{BE}=\vec{IF}$ :

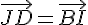
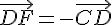
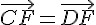
– Puisque $\vec{JD}=\vec{BI}$ , d’après la construction, et $\vec{DF}=-\vec{CD}$ et $\vec{CF}=\vec{DF}$ ,

il en résulte que :

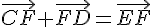
$\vec{CF}+\vec{FD}=\vec{EF}$

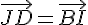
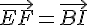
Ensuite, comme $\vec{JD}=\vec{BI}$ et E et F sont symétriques de J et D, alors $\vec{EF}=\vec{BI}$ .

– De même pour 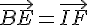$\vec{BE}=\vec{IF}$ , car les symétriques de B et I par rapport à C sont E et F.

Conclusion :

Les côtés opposés du quadrilatère BIEF sont égaux deux à deux, d’où BIEF est un parallélogramme.

Exercice 2 – démontrer que des droites sont parallèles.

a) Placement des points :

On place les points D, E, F et G tels que 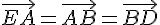$\vec{EA}=\vec{AB}=\vec{BD}$

et les segments [AG] et [BF] ont le même milieu C.

b) On doit montrer que 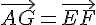$\vec{AG}=\vec{EF}$ .

Comme C est le milieu des segments [AG] et [BF], les vecteurs $\vec{AC} = \vec{CG}et \vec{BC} = \vec{CF}$ .

Cela implique que 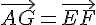$\vec{AG}=\vec{EF}$ car G et F sont symétriques par rapport à C.

c) Montrer que les droites (BF) et (DG) sont parallèles :

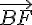
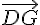
Les vecteurs $\vec{BF}$ et $\vec{DG}$ sont colinéaires si et seulement si les segments [BF] et [DG] sont parallèles.

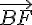
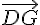
Puisque $\vec{BF}$ = $\vec{DG}$ , les droites (BF) et (DG) sont parallèles.

d) Montrer que les droites (AF) et (BG) sont parallèles :

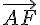
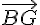
Les vecteurs $\vec{AF}$ et $\vec{BG}$ sont colinéaires.

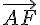
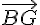
En effet, puisque $\vec{AF}$ est colinéaire à $\vec{BG}$ par construction (étant donné que F et G sont les symétriques par rapport à C,

les droites (AF) et (BG) sont parallèles.

Exercice 3 – vecteurs égaux dans un parallélogramme.

a) Vecteurs égaux :

Dans le parallélogramme , les vecteurs opposés sont égaux :

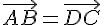
$\vec{AB}=\vec{DC}$

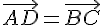
$\vec{AD}=\vec{BC}$

Pour les symétriques par rapport à un point :

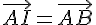
$\vec{AI}=\vec{AB}$

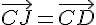
$\vec{CJ}=\vec{CD}$

b) Montrons que 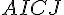est un parallélogramme :

Nous devons montrer que les segments sont égaux et parallèles pour former un parallélogramme.

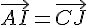
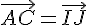
Comme $\vec{AI}=\vec{CJ}$ et $\vec{AC}=\vec{IJ}$ , nous avons bien les conditions d’un parallélogramme.

Donc 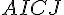est un parallélogramme.

Exercice 4 – les coordonnées du vecteur.

Pour déterminer les coordonnées du vecteur 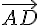$\vec{AD}$ , nous devons soustraire les coordonnées de A à celles de D.

A a pour coordonnées (-1, 2), et D a pour coordonnées (4, 1).

Les coordonnées du vecteur 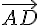$\vec{AD}$ sont calculées comme suit :

X :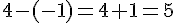

Y :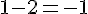

Les coordonnées du vecteur 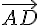$\vec{AD}$ sont donc :

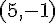
La bonne réponse est : a.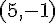

Exercice 5 – calculer les coordonnées du vecteur.

Énoncé : Dans un repère orthonormé, le point A a pour coordonnées (3 ; -2) et le point B (2 ; 4).

Les coordonnées du vecteur 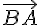$\vec{BA}$ sont données par la formule :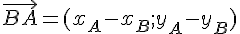

Formule : $\vec{BA}=(x_A-x_B;y_A-y_B)$

Calcul :

1. Calcul de la coordonnée en :

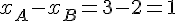
2. Calcul de la coordonnée en :

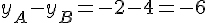
Les coordonnées du vecteur 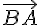$\vec{BA}$ sont (1 ; -6), soit l’option c.

Exercice 6 – les vecteurs colinéaires.

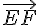
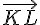
Les vecteurs colinéaires sont $\vec{EF}$ et $\vec{KL}$ . Ils ont la même direction.

Exercice 7 – conditions pour des vecteurs colinéaires.

Pour que les deux vecteurs $\vec{u}$ et $\vec{v}$ soient colinéaires, il faut que :

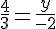
$\frac{4}{3}=\frac{y}{-2}$

On résout l’équation :

$4\times (-2)=3\times y$

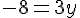
Donc :

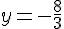
$y=-\frac{8}{3}$

Conclusion :

La valeur de pour laquelle les vecteurs sont colinéaires est option aucune des propositions données.

Exercice 8 – simplifier des écritures vectorielles.

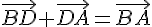
1) $\vec{BD}+\vec{DA}=\vec{BA}$

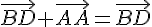
2) $\vec{BD}+\vec{AA}=\vec{BD}$

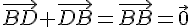
3) $\vec{BD}+\vec{DB}=\vec{BB}=\vec{0}$

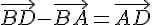
4) $\vec{BD}-\vec{BA}=\vec{AD}$

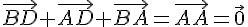
5) $\vec{BD}+\vec{AD}+\vec{BA}=\vec{AA}=\vec{0}$

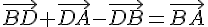
6) $\vec{BD}+\vec{DA}-\vec{DB}=\vec{BA}$

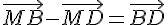
1) $\vec{MB}-\vec{MD}=\vec{BD}$

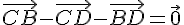
2) $\vec{CB}-\vec{CD}-\vec{BD}=\vec{0}$

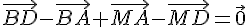
3) $\vec{BD}-\vec{BA}+\vec{MA}-\vec{MD}=\vec{0}$

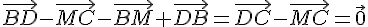
4) $\vec{BD}-\vec{MC}-\vec{BM}+\vec{DB}=\vec{DC}-\vec{MC}=\vec{0}$

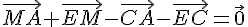
5) $\vec{MA}+\vec{EM}-\vec{CA}-\vec{EC}=\vec{0}$

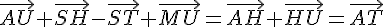
6) $\vec{AU}+\vec{SH}-\vec{ST}+\vec{MU}=\vec{AH}+\vec{HU}=\vec{AT}$

Exercice 9 – vecteur et coordonnées.

1. Calcul de $3\vec{u} - 2\vec{v}$ :

Les coordonnées de sont (-5, 8) et celles de $\vec{v}$ sont (3, 5).

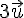
Calculons $3\vec{u}$ :

$3\vec{u} = 3 \times ( -5; 8 ) = ( 3 \times -5 ; 3 \times 8 ) = ( -15 ;24)$

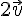
Calculons $2\vec{v}$ :

$2\vec{v} = 2 \times ( 3 ;5) =( 2 \times 3 ; 2 \times 5) = ( 6 ; 10)$

Calculons $3\vec{u} - 2\vec{v}$ :

$3\vec{u} - 2\vec{v} = ( -15 ; 24 )- ( 6 ; 10) = ( -15 - 6 ; 24 - 10 ) = ( -21 ;14 )$

Donc, le vecteur $3\vec{u} - 2\vec{v}$ a pour coordonnées : ( -21; 14 ).

La réponse correcte est : d.( -21 ; 14 )

Exercice 10 – parallélogramme et égalités.

Dans un parallélogramme, les côtés opposés sont égaux et parallèles. Par conséquent :

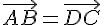
$\vec{AB}=\vec{DC}$

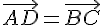
$\vec{AD}=\vec{BC}$

Les choix corrects sont donc b et d.

4.7/5 - (33603 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «vecteurs : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Les équations et inéquations

L’étude de fonction

Intervalles et valeur absolue

Inéquations

Trigonométrie

Statistiques

Algorithmes et programmes

Résolution graphique d’équations et inéquations

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 357 907 cours et exercices de maths téléchargés en PDF et 4 250 exercices.