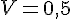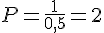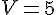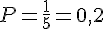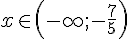Fonction inverse : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Exercice 1 – inverse d’un nombre.
a)
Pour 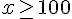
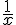
Donc, 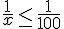
b)
Pour 
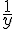
Donc, 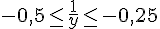
Exercice 2 – courbe d’une fonction inverse.
La courbe représente la fonction inverse 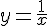
À partir du graphique, on observe que pour 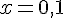
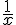
Pour 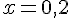
En utilisant le graphe :
Pour 
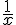
Donc, la bonne réponse est d)
Exercice 3 – tableau et étudier le signe de l’expression.
a) Recopier et compléter :
Pour tout 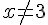
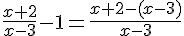
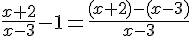
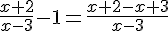
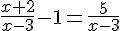
b) En déduire le tableau de signes de 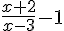
Tableau de signes :
La fraction 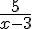

Pour 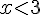

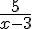
Pour 

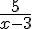
Exercice 4 – résistance équivalente et fonction inverse.
1. On note 
a) Démontrer que la valeur de la résistance équivalente 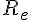
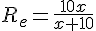
Étant donné que 

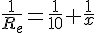
En combinant les fractions :
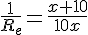
En inversant :
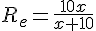
b) Afficher à l’écran de la calculatrice la courbe représentative de la fonction 
![[0 ; 10]](https://maths-pdf.fr/latex-images/cb55360cc7b731d1408aae4aaa3a86a2.png)
Utilisez une calculatrice graphique pour tracer la courbe de 
![[0 ; 10]](https://maths-pdf.fr/latex-images/cb55360cc7b731d1408aae4aaa3a86a2.png)
2. Déterminer les valeurs de 
a) Graphiquement :
Tracez la droite 


b) Algébriquement :
On résout l’inéquation 
Mise sous forme d’inéquation :
Développer et simplifier :
En soustrayant 4x des deux côtés :
En divisant par 6 :
Donc, 

Exercice 5 – calculatrice et étude des courbes avec conjecture.
a) Affichage des courbes :
Utilisez votre calculatrice pour tracer les courbes de f et g dans la fenêtre indiquée.
Vous observerez que la courbe de f tend vers la droite de g sauf en x = 1 où f n’est pas définie.
b) Conjecture :
Pour toutes les valeurs de 

c) Démonstration :
En calculant 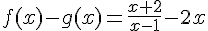
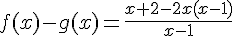
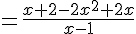
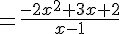
En analysant ce résultat, vous pourrez conclure que l’ensemble des solutions de l’inéquation est bien 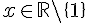
Exercice 6 – etude d’un piston et fonction inverse.
a) Expliquer pourquoi cette loi est liée à la fonction inverse.
La relation 
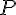

Cela signifie que si l’un augmente, l’autre diminue en conséquence pour maintenir le produit constant.
Ceci est typique d’une fonction inverse où l’on a 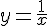
b) Quelles sont les valeurs possibles pour la pression ?
Étant donné 

- Quand
- Quand
Donc, les valeurs possibles pour la pression 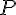
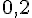
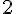
Exercice 7 – exprimer des longueurs et aire d’un triangle.
a) Exprimer les longueurs ON et MN en fonction de x.
La longueur ON est simplement la coordonnée 
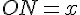
La longueur MN est la différence entre les ordonnées de M et N :
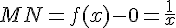
b) Démontrer que l’aire du triangle OMN est constante.
L’aire du triangle OMN peut être calculée par la formule de l’aire d’un triangle rectangle :
En substituant les valeurs des longueurs obtenues plus haut, on a :
En simplifiant, on trouve :
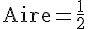
Donc, l’aire du triangle OMN est constante et vaut 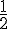
Exercice 8 – résoudre des inéquations et intervalles.
a) Résoudre 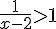
![\left]2,+\infty\right[](https://maths-pdf.fr/latex-images/6e9f1b6c3d9586868fe0606704a5c64d.png)
Transformons l’inéquation :
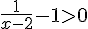
Cela devient :
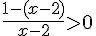
Soit :
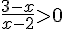
Analysons le signe de cette fraction.
Nous devons avoir 

– 
– 
Donc, la solution dans l’intervalle donné est :
Solution : ![\left]2,3\right[](https://maths-pdf.fr/latex-images/f289139313e3e3c7f8ae878244158f9b.png)
b) Résoudre 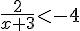
![\left]-\infty,-3\right[](https://maths-pdf.fr/latex-images/cfa5a3f4c7b52b05f5353c0bb6753113.png)
Transformons l’inéquation :
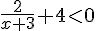
Multiplions le tout par x+3 (qui est négatif puisque x < -3) :
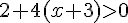
Développons :
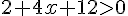
Simplifions :
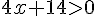
Donc :
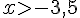
La solution dans l’intervalle donné est :
Solution : ![\left]-3,5,-3\right[](https://maths-pdf.fr/latex-images/81fa8f137efc625e47523b75ec7576aa.png)
Exercice 9 – résoudre une inéquation et étude d’un quotient.
a) Étude du signe du quotient :
Pour étudier le signe de 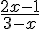
Numérateur : 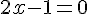
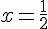
Dénominateur : 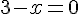
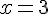
Les valeurs critiques sont donc 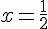
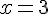
| 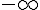
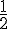
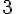

| Zone | — | Plus | — | Moins | — | Plus |
b) Résolution de l’inéquation :
Résoudre 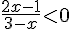
D’après le tableau de signes, cela se produit lorsque 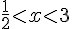
c) Vérification graphique avec la calculatrice :
En traçant le graphe de la fonction 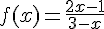
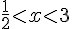
Exercice 10 – calcul formel et fonction inverse.
Pour résoudre l’inéquation 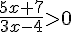
1. Trouvons les valeurs annulant le numérateur : 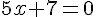
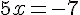
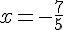
2. Trouvons les valeurs annulant le dénominateur : 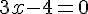
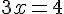
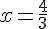
3. Les valeurs critiques sont donc 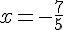
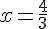
4. Analyse de signe :
- Pour
- Pour
- Pour
5. La solution de l’inéquation est donc ![x\in]-\infty;-\frac{7}{5}]\cup[\frac{4}{3};+\infty[](https://maths-pdf.fr/latex-images/2093bde431f68c197520fbdb4ae9d77a.png)
Télécharger ou imprimer cette fiche «fonction inverse : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.