Les équations et inéquations : corrigé des exercices de maths en 2de en PDF

Exercice 1 – tableau de signe d’une fonction affine.

a) Tableau de signes de

La fonction affine telle que s’annule lorsque :

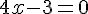
Soit :

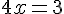
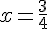
Le tableau de signes est :

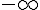
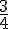
		0

b) Résolution de l’inéquation :

Nous avons :

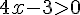
Cela revient à :

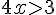
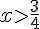
La solution est donc :

Exercice 2 – fonction affine et tableau de signes.

a) On cherche le tableau de signes de la fonction .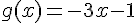

Cette fonction est décroissante car le coefficient de est négatif.

Pour trouver le zéro de la fonction, on résout :

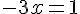
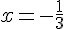
Le tableau de signes est donc :

	-∞	–	+∞
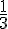
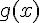
	–	0	+

b) Céline affirme : « Sans calcul, je peux donner le signe de .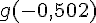
Est-ce possible ?

Oui, c’est possible car 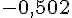est inférieur à .
Donc, .

c) Déterminer du tableau de signes la résolution de chaque inéquation :

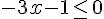
Selon le tableau de signes, la solution est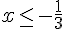

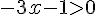
Selon le tableau de signes, la solution est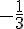

Exercice 3 – deux fonctions affines et des affirmations vraies ou fausses.

1. Donner le tableau de signes :

a) de :

L’équation de est .

Cherchons le zéro de :

.

Tableau de signes :

b) de :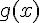

L’équation de \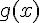 est .

Cherchons le zéro de :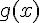

.

Tableau de signes :

2. Pour chaque affirmation, dire si elle est vraie ou fausse :

a) Elie : « Je peux dire que \(f(0,982)\) est positif sans effectuer de calcul. »

Vrai.

Car  0,982 < 1  et d’après le tableau de signes, pour  x < 1 ,  f(x)  est positif.

b) Quentin : « Il existe un nombre réel inférieur à 2 dont l’image par est positive. »

Vrai. Pour x < 1, f(x) est positif.

Donc, par exemple pour  x = 0, f(x) = 5 ce qui est positif.

c) Karen : « Pour tout nombre réel x négatif, son image g(x) est négative. »

Vrai. Pour x < 0, g(x) est négatif car 0 < 0,6 et d’après le tableau de signes, g(x) est négatif pour x < 0,6.

d) Geoffroy : « Il existe des nombres réels x tels qu’à la fois f(x) et g(x) sont positifs. »

Faux. Selon les tableaux de signes, f(x) est positif pour x 0,6.

Il n’y a pas d’intersection où les deux fonctions sont positives simultanément.

Exercice 4 – système de deux équations à deux inconnues.

a) Expliquer pourquoi ce système (S) a un seul couple solution :

Pour déterminer si ce système a un seul couple solution, nous devons vérifier la régularité des coefficients des deux équations.

Le système est donné par :

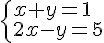
Les coefficients directeurs des équations sont différents :

– Premier équation :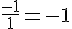

– Deuxième équation :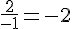

Les coefficients étant différents, les droites sont sécantes et le système a un seul couple solution.

b) Résoudre ce système :

Pour résoudre le système, utilisons la méthode de substitution.

Exprimons à partir de la première équation :

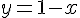
Substituons cette expression dans la deuxième équation :

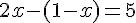
Simplifions et résolvons pour :

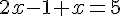
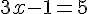
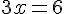
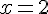
Utilisons cette valeur de pour trouver :

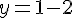
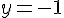
Le couple solution est donc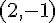

Exercice 5 – programme de calcul et équations.

Soit le nombre choisi.

1. Ajouter 8 :

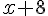
2. Multiplier le résultat par 3 :

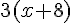
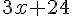
3. Enlever 24 :

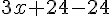
4. Enlever le nombre de départ :

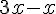
Conclusion :

La conjecture est vraie.

Pour n’importe quel nombre choisi, on trouve le double de ce nombre.

Exercice 6 – trois triangles équilatéraux identiques découpés dans les coins.

Trois triangles équilatéraux identiques sont découpés dans les coins d’un triangle équilatéral de côté 6 cm.

Gabriel émet une conjecture :

« La somme des périmètres des trois petits triangles équilatéraux est égale au périmètre de l’hexagone orange. »

Cette conjecture est-elle vraie ? Justifier.

Chaque petit triangle équilatéral découpé a un côté qui est un tiers du côté du grand triangle.

Ainsi, le côté de chaque petit triangle est :

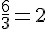
Le périmètre de chaque petit triangle équilatéral est :

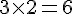
La somme des périmètres des trois petits triangles est :

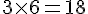
L’hexagone est formé par les côtés restants du grand triangle (côté 6 cm) après avoir découpé les trois petits triangles équilatéraux.

Ainsi, chaque côté de l’hexagone est aussi 2 cm, et l’hexagone a 6 côtés.

Le périmètre de l’hexagone est :

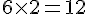
Conclusion : La somme des périmètres des trois petits triangles est 18, tandis que le périmètre de l’hexagone est 12.

Donc, la conjecture de Gabriel est fausse.

Exercice 7 – nombre de départ et programme de calcul.

a) Si on choisit le nombre -4 :

– On soustrait 3 :

– On élève -7 au carré :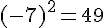

– On soustrait le carré du nombre de départ :

On obtient 33.

b) Pour obtenir 0, effectuons le calcul :

– Soit le nombre de départ.

– Alors :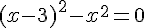

– Cela donne :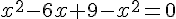

– Ce qui simplifie à :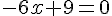

– Résolvons :

Oui, il est possible de choisir le nombre 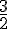pour obtenir 0.

Exercice 8 – deux programmes de calcul et une affirmation.

a) Joseph affirme :

Pour le premier programme :

Choisissons un nombre .

Appliquons les opérations : multiplier par 2 et ajouter 1.

Cela donne .

Pour le second programme :

Choisissons un nombre .

Appliquons les opérations : ajouter 1, élever au carré, puis soustraire le carré du nombre de départ.
Cela donne :

.

Donc, les deux programmes donnent le même résultat quel que soit le nombre choisi pour .

Joseph a raison.

b) Est-il possible d’obtenir 0 ?

Non, le résultat des deux programmes est toujours .
Puisque pour tout réel, il est impossible d’obtenir 0.

Exercice 9 – algorithme et formule d’abonnement à un club.

Pour déterminer la formule la moins chère, nous allons comparer les deux options en fonction du nombre de films téléchargés .

Formule A : Le coût total est .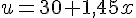

Formule B : Le coût total est .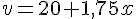

En comparant :

Si 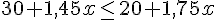alors Formule A est la moins chère.

Sinon, Formule B est la moins chère.

Pour résoudre l’inéquation :

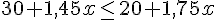
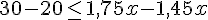
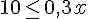
Donc, pour , Formule B est la moins chère.
Pour , Formule A est la moins chère.

Exercice 10 – conjecture et programmes de calcul.

1. Quel nombre obtient-on avec chaque programme lorsqu’on choisit :

a) -1 ?

Programme 1 :

– Choisir un nombre :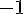

– Soustraire 1 :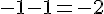

– Élever au carré :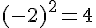

– Multiplier par 4 :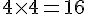

– Soustraire 1 :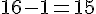

Résultat : 15

Programme 2 :

– Choisir un nombre :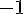

– Multiplier par 2 et soustraire 1 :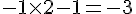

– Multiplier le nombre choisi par 2 et soustraire 3 :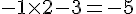

– Multiplier les deux nombres trouvés :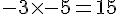

Résultat : 15

b) 0 ?

Programme 1 :

– Choisir un nombre :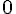

– Soustraire 1 :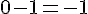

– Élever au carré :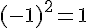

– Multiplier par 4 :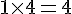

– Soustraire 1 :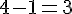

Résultat : 3

Programme 2 :

– Choisir un nombre :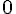

– Multiplier par 2 et soustraire 1 :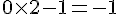

– Multiplier le nombre choisi par 2 et soustraire 3 :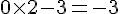

– Multiplier les deux nombres trouvés :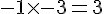

Résultat : 3

c) 1 ?

Programme 1 :

– Choisir un nombre :

– Soustraire 1 :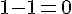

– Élever au carré :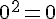

– Multiplier par 4 :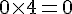

– Soustraire 1 :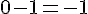

Résultat : -1

Programme 2 :

– Choisir un nombre :

– Multiplier par 2 et soustraire 1 :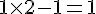

– Multiplier le nombre choisi par 2 et soustraire 3 :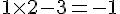

– Multiplier les deux nombres trouvés :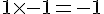

Résultat : -1

d) 2 ?

Programme 1 :

– Choisir un nombre :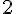

– Soustraire 1 :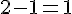

– Élever au carré :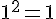

– Multiplier par 4 :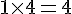

– Soustraire 1 :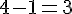

Résultat : 3

Programme 2 :

– Choisir un nombre :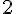

– Multiplier par 2 et soustraire 1 :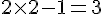

– Multiplier le nombre choisi par 2 et soustraire 3 :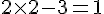

– Multiplier les deux nombres trouvés :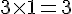

Résultat : 3

2. a) Émettre une conjecture quant à ces deux programmes.

La conjecture est que les deux programmes de calcul donnent toujours le même résultat pour un nombre choisi.

b) Démontrer cette conjecture.

Soit  x   le nombre choisi.

Programme 1 :

– Soustraire 1 :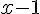

– Élever au carré :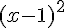

– Multiplier par 4 :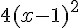

– Soustraire 1 :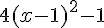

Programme 2 :

– Multiplier par 2 et soustraire 1 :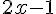

– Multiplier par 2 et soustraire 3 :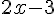

– Multiplier les deux résultats :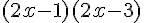

Calculons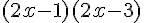

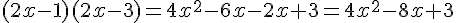
Comparons les deux résultats :

Programme 1 :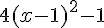

Programme 2 :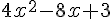

Développons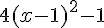

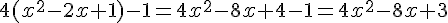
Les deux programmes donnent le même résultat, ce qui vérifie la conjecture.