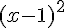Résolution graphique d’équations et inéquations : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Exercice 1 – résoudre graphiquement les inéquations.
a) 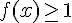
Pour 
![\left[0,5;1\right]](https://maths-pdf.fr/latex-images/fb708d766f87010d1a215fdffdb2b730.png)
b) 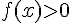
Pour 
![\left]-3;1,5\right[](https://maths-pdf.fr/latex-images/ae517074788b3cce2f4e0acd621f07a7.png)
c) 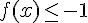
Pour 

Exercice 2 – réssoudre les inéquations graphiquement.
a) 
Il faut identifier les zones où la courbe 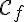
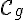
On observe que cela se produit pour ![x\in[-3;-1]](https://maths-pdf.fr/latex-images/6875110367777533205f38e004fa3bd6.png)
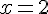
b) 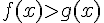
Ici, on cherche les zones où la courbe 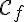
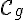
Cela se produit pour 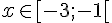
c) 
Nous devons déterminer les intervalles où la courbe 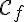
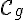
Ces conditions sont vérifiées pour ![x\in[-1;2]](https://maths-pdf.fr/latex-images/3ae08c9801493bea84eafd9741455d07.png)
Exercice 3 – problème sur les fonctions et inéquations.
a) Montrer que pour tout 
L’aire du carré ABCD est 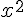
Le carré AEFG a pour côté 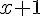
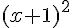
L’aire du polygone BCDGFE est alors :
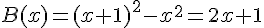
b) À l’écran de la calculatrice, afficher les courbes représentatives des fonctions 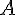
La fonction 
La fonction 
c) Vérifier l’affichage obtenu avec un logiciel de calcul formel.
En utilisant un logiciel de calcul formel, on observe l’intersection des graphes au niveau des racines des équations données.
Les racines sont 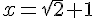
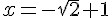
d) Déduire des questions b) et c) les solutions de l’inéquation 
En résolvant l’inéquation 

Exercice 4 – déterminer l’image et l’antécédent.
a) Déterminer l’image par f de :
b) Déterminer l’antécédent de 0,6 par f :
L’antécédent de 0,6 par f est 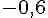
c) Existe-t-il un nombre égal à son image par f ?
Oui, le nombre 0 est égal à son image par f, car son opposé est lui-même : 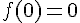
Exercice 5 – résolution graphique d’inéquation.
a) Ensembles de définition :
– Pour la fonction f, le domaine est ![[0\,;2]](https://maths-pdf.fr/latex-images/c39d5b24204494e0b3896e5b674ad0b7.png)
– Pour la fonction g, le domaine est ![[0\,;3]](https://maths-pdf.fr/latex-images/200e05b4d32eae6ef2c373b1b614d43b.png)
b) Validation de l’affirmation :
Linda affirme : «g(1) > f(1)».
Pour vérifier cette affirmation, regardons les valeurs de f et g pour 
– f(1) se lit graphiquement comme étant 
– g(1) se lit graphiquement comme étant 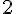
On a 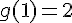
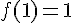
Donc, f(1) » alt= »g(1)>f(1) »>, Linda a raison.
Exercice 6 – lecture graphique d’une fonction.
a) L’image de 2 par f est : 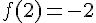
b) f(4) est : 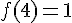
c) Les antécédents de 2 par f sont :
d) Reformulez b) : l’image de 4 par f est 1.
Reformulez c) : les antécédents de 2 par f sont -3 et 1.
Exercice 7 – problème de carré et fonctions.
a) Ensemble de définition des fonctions A et P :
L’ensemble de définition pour les fonctions A(x) et P(x) est 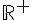
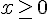
b) Exprimer A(x) et P(x) en fonction de x :
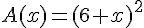
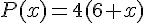
c) Calculer P(x) lorsque A(x) = 51,84 :
Équation : 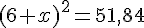
Résolution : 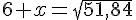
Environ : 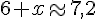
Donc, 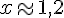
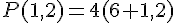
Val = 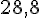
d) Calculer A(x) lorsque P(x) = 32,8 :
Équation : 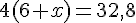
Résolution : 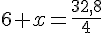
Environ : 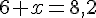
Donc, 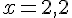
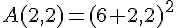
Val = 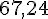
Exercice 8 – tableau de valeurs d’une fonction.
a) Parmi les expressions proposées:
Nous vérifions chaque expression pour les valeurs données. La seule expression qui convient à toutes les valeurs du tableau est 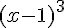
b) En sachant que 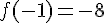
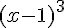
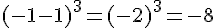
c) La formule saisie dans la cellule B2 est 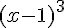
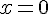
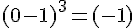
Exercice 9 – représenter des intervalles.
a) 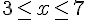
b) 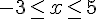
c) 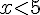
d) 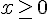
e) 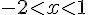
f) 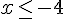
a) 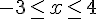
b) 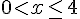
c) 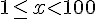
d) ![x\in{}]-\infty;10[](https://maths-pdf.fr/latex-images/9179517dbfa75d1a3ec0045d2cf6c261.png)
e) 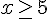
f) ![x\in{}]-\infty;0[](https://maths-pdf.fr/latex-images/113a0ad9395be932375c6e2b171828e9.png)
Exercice 10 – ensemble de définition, image et antécédent.
a) Déterminer l’ensemble de définition de V.
L’ensemble de définition de la fonction V est constitué des valeurs possibles pour x.
Ainsi, l’ensemble de définition est 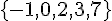
b) Lire l’image de 3 par V.
L’image de 3 par la fonction V est 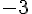
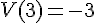
c) Lire V(7).
La valeur de V(7) est 
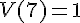
d) Lire les antécédents de 7 par V.
Les antécédents de 7 par la fonction V sont 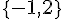
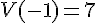
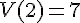
Télécharger ou imprimer cette fiche «résolution graphique d'équations et inéquations : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.