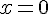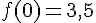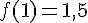L’étude de fonction : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Dans cet article, nous vous proposons des corrections d’exercices de mathématiques axées sur l’étude de fonction, un sujet fondamental pour les élèves de seconde. Comprendre les fonctions est essentiel pour développer des compétences mathématiques cruciales, telles que l’analyse de graphes, le calcul de dérivées et l’interprétation de résultats. En maîtrisant ces concepts, les élèves pourront non seulement exceller en seconde, mais aussi se préparer efficacement pour les défis futurs en mathématiques.
Exercice 1 – décrire le sens de variation.
a) Description du sens de variation de la fonction 
Pour x variant de -4 à -1, h(x) décroît de 4 à -1.
Pour x variant de -1 à 1, h(x) croît de -1 à 3.
Pour x variant de 1 à 3, h(x) décroît de 3 à 0.
b) Comparaisons :
Comparons h(0) et h(1) : Étant donné que la fonction est croissante entre -1 et 1, on déduit h(0) < h(1).
Comparons h(2) et h(2,5) : Étant donné que la fonction est décroissante entre 1 et 3, on déduit h(2) > h(2,5).
c) Tracé d’une courbe possible :
Pour tracer une courbe représentative de 
Exercice 2 – lire le maximum et le minimum.
Intervalle a) [-2 ; 0]
Le maximum est atteint pour x = -2 avec y = 0.
Le minimum est atteint pour x = -1 avec y = -3.
Intervalle b) [0 ; 4]
Le maximum est atteint pour x = 1 avec y = 2.
Le minimum est atteint pour x = 2 avec y = -2.
Intervalle c) [-2 ; 4]
Le maximum est atteint pour x = 1 avec y = 2.
Le minimum est atteint pour x = -1 avec y = -3.
Intervalle d) [2 ; 4]
Le maximum est atteint pour x = 4 avec y = 1.
Le minimum est atteint pour x = 2 avec y = -2.
Exercice 3 – tableau de variation et justification.
a) Pour tout nombre réel x de [-7 ; 3], justification :
La fonction f est croissante sur l’intervalle [-7 ; -3] allant de 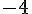
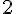
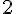
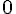
Donc, 
b) Pour tout nombre réel x de [-3 ; 5], justification :
La fonction f est décroissante sur l’intervalle [-3 ; 3] de 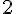
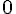
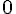
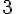
Donc, 
Exercice 4 – encadrement d’images.
a) Pour tout nombre réel x de [-2 ; 3],
b) Pour tout nombre réel x de [0 ; 3],
Exercice 5 – tableau de variation de fonctions affines.
Pour chaque fonction affine de la forme 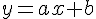

- Si a > 0, la fonction est croissante.
- Si a < 0, la fonction est décroissante.
Pour la fonction f : 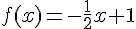
Le coefficient directeur est 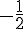
Pour la fonction g : 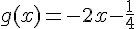
Le coefficient directeur est 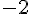
Pour la fonction h : 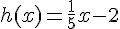
Le coefficient directeur est 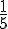
Pour la fonction k : 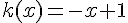
Le coefficient directeur est 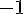
Exercice 6 – droites et représentation graphique.
a) La fonction m est définie par 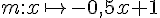
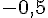
La pente de la droite 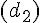
La droite 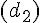
La réponse de Andréa est incorrecte.
b)- La fonction j : 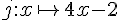
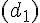
– La fonction k : 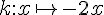
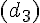
– La fonction l : 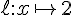
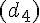
– La fonction m : 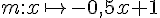
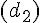
Exercice 7 – associer fonction et tableau de variation.
a) Tracé de la courbe :
Pour tracer la courbe, on suit les variations de la fonction g données dans le tableau :
– Pour ![x\in[-1;0]](https://maths-pdf.fr/latex-images/c579bdfac8698e3da4d034b3c8576044.png)
– Pour ![x\in[0;3]](https://maths-pdf.fr/latex-images/2ed5d3e5d0bfd33c49b3a23b8716f873.png)
– Pour ![x\in[3;4]](https://maths-pdf.fr/latex-images/3fdae577a2e9d98237c1d66fa0c07517.png)
– Pour ![x\in[4;6]](https://maths-pdf.fr/latex-images/e526d88dbdd846d110ea0e79091dfff0.png)
b) Nombres réels avec image négative ou nulle :
Les valeurs de 
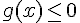
– ![x\in[2;4]](https://maths-pdf.fr/latex-images/3753a5da8e65f88e30f116380087f898.png)
Exercice 8 – déterminer les nombres réels et images d’une fonction.
Les valeurs de x pour lesquelles l’image par la fonction h est supérieure ou égale à 2 sont :
1. Pour 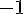
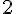
2. Pour 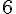
Il n’y a pas d’autres valeurs de x dans l’intervalle donné pour lesquelles h(x) est supérieur ou égal à 2.
Exercice 9 – problème d’un trapèze et fonctions.
a) Observer la figure et conjecturer le sens de variation de f :
En observant la figure, on remarque que lorsque le point M se déplace de A vers B, l’aire du domaine coloré semble diminuer.
b) Exprimer f(x) en fonction de x dans chacun des cas :
Pour ![x \in [0; 5]](https://maths-pdf.fr/latex-images/8f25a17509a52bcffb6f734cef9ca1c9.png)
Dans cette plage, la zone colorée est un rectangle. Sa hauteur est toujours 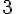

Donc :
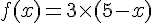
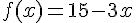
Pour ![x \in [5; 8]](https://maths-pdf.fr/latex-images/6b91d32a255e5c31732ba8a105a6ceef.png)
Dans cette plage, la zone colorée est un trapèze. Sa grande base est 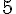

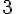
Donc :
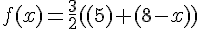
En simplifiant l’expression :
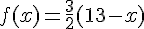
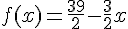
Exercice 10 – dresser le tableau de variation.
a) La fonction 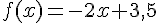
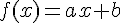
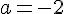
La pente 

Le tableau de variation est donc :
| x | f(x) | |
|---|---|---|
| -∞ | +∞ | |
| décroît | +∞ vers -∞ | |
b) Pour tracer la courbe représentative de 
- Pour
- Pour
La ligne reliant ces points montre une réduction constante, confirmant la décroissance définie dans le tableau de variation.
Télécharger ou imprimer cette fiche «l'étude de fonction : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.