Les équations de droites : corrigé des exercices de maths en 2de en PDF

Mis à jour le 24 novembre 2025

Les équations de droites constituent un concept fondamental en maths pour les élèves de seconde. Maîtriser ce sujet permet non seulement de résoudre des problèmes géométriques, mais aussi de développer des compétences analytiques essentielles. Dans cet article, nous corrigerons des exercices pratiques qui aideront les élèves à mieux comprendre les droites, leur représentation graphique et les applications des équations linéaires. Investir du temps sur ce thème renforcera leur confiance en mathématiques et facilitera leur parcours académique.

Exercice 1 – vérifier qu’un point appartient à une droite.

1) Équation: 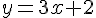$y=3x+2$

Pour le point C(3;7) :

Calculons 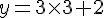$y=3\times 3+2$

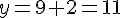
Donc, C(3;7) n’appartient pas à cette droite.

2) Équation: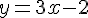

Pour le point C(3;7) :

Calculons 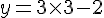$y=3\times 3-2$

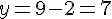
Donc, C(3;7) appartient à cette droite.

3) Équation: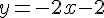

Pour le point C(3;7) :

Calculons 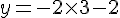$y=-2\times 3-2$

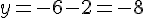
Donc, C(3;7) n’appartient pas à cette droite.

4) Équation: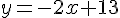

Pour le point C(3;7) :

Calculons 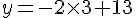$y=-2\times 3+13$

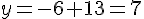
Donc, C(3;7) appartient à cette droite.

Exercice 2 – trouver deux nombres dont la différence.

1) Soit x et y les deux nombres. On a les équations suivantes :

x – y = 7

x² – y² = 21

On sait que x² – y² = (x-y)(x+y) .

Donc :

$21 = 7 \times (x+y)$

On a $x+y = \frac{21}{7} = 3$ .

On résout le système :

$\begin{cases} x - y = 7 \\ x + y = 3 \end{cases}$

En additionnant les deux équations, on obtient :

2x = 10 soit x = 5

En substituant x = 5 dans x + y = 3, on trouve :

5 + y = 3 soit y = -2

Les deux nombres sont donc 5 et -2.

2) Algorithme proposé :

1. Soit d la différence des deux nombres $( x - y )$ et D la différence de leurs carrés $( x^2 - y^2 )$ .

2. Calculer x+y = \frac{D}{d} .

3. Résoudre le système :

$\begin{cases} x - y = d \\ x + y = \frac{D}{d} \end{cases}$

4. Trouver x en additionnant les deux équations :

$2x = d + \frac{D}{d}$ donc $x = \frac{d + \frac{D}{d}}{2}$

5. Trouver y en substituant x dans l’une des équations :

$y = x - d$

Cet algorithme permet de retrouver les deux nombres.

Exercice 3 – problème de géométrie avec un triangle rectangle.

1) Calculer le produit de ces deux longueurs :

Soit a et b les longueurs des côtés de l’angle droit.

L’aire du triangle rectangle est donnée par :

$\frac{1}{2}\times a\times b=8,64$

Donc : $a\times b=17,28$

2) Utiliser le théorème de Pythagore pour calculer la somme de leur carré :

Comme le triangle est inscrit dans le demi-cercle, son diamètre AB est l’hypoténuse et vaut 6 cm (deux fois le rayon).

Selon Pythagore, on a :

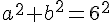
Donc :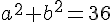

3) Utiliser les identités remarquables pour calculer le carré de leur somme et le carré de leur différence :

On sait que :

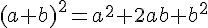
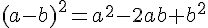
4) Calculer leur somme et leur différence :

On a deux équations :

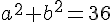
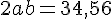
Résolvons pour (a+b)² et (a-b)² et en déduisant leurs valeurs :

$(a+b)^2 = 36 + 34,56$

$(a-b)^2 = 36 - 34,56$

5) Résoudre le système formé de ces deux expressions :

$a+b = \sqrt{70,56}et a-b = \sqrt{1,44}$

On résout :
$a+b = 8,4$
$a-b = 1,2$

D’où, par addition et soustraction :

$a = \frac{8,4 + 1,2}{2} = 4,8$

$b = \frac{8,4 - 1,2}{2} = 3,6$

6) Conclure :

Les longueurs des côtés de l’angle droit du triangle rectangle sont a = 4,8 cm et b = 3,6 cm.

Exercice 4 – montrer que les points A, B et C sont alignés.

Pour montrer que les points A , B et C sont alignés, nous devons montrer qu’ils sont colinéaires.

Cela est lié au théorème de Ménélaüs.

Calculons les coordonnées des points d’intersection.

Point A à l’intersection des droites 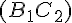et :

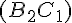
Les équations des droites sont obtenues à partir des coordonnées des points.

Soit la droite :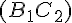

Direction $(x-1,y-1) = t(6,-4)$

Pour la droite :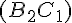

Direction $(x-4,y+3) = s(3,9)$

Pour trouver l’intersection, nous résolvons :

$\begin{cases} x - 1 = t \cdot 6 \\ y - 1 = t \cdot (-4) \\ x - 4 = s \cdot 3 \\ y + 3 = s \cdot 9 \end{cases}$

Afin de simplifier, nous égalerons les valeurs de et trouvées de chacune des équations.

Similairement, nous procédons pour les autres points.

En termes de colinéarité:

$\vec{AB} = \vec{AC}$

En résolvant ces équations paramétriques, on vérifie que le déterminant suivant est nul :

$\begin{vmatrix} x_B - x_A x_C - x_A \\ y_B - y_A y_C - y_A \end{vmatrix} = 0$

Donc les points A, B, et C sont colinéaires et alignés.

Exercice 5 – problème et salle de spectacle.

Partie A :

1) La relation entre x et y si Emma dépense la totalité de son bon est :

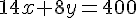
2) x ne peut pas être égal à y car le coût unitaire des pièces et des films est différent. Ainsi, s’ils étaient égaux, Emma dépasserait son budget ou ne l’épuiserait pas complètement.

3) Pour construire la représentation graphique, vous devez tracer la droite de l’équation :

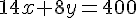
4) Les points de la représentation qui ont des coordonnées entières sont :

(20, 0) : Emma ne regarde que des pièces de théâtre.
(0, 50) : Emma ne regarde que des films.
Vérifier d’autres combinaisons avec des x et y entiers.

5) Pour voir presque autant de films que de pièces, Emma peut choisir par exemple (17, 1), car :

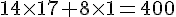
$14\times 17+8\times 1=400$

Partie B :

1) Pour qu’Emma voie deux fois plus de films que de pièces, tracer la droite représentant :

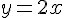
2) En remplaçant y dans l’équation de la partie A :

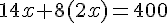
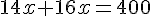
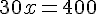
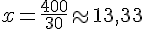
$x=\frac{400}{30}\approx13,33$

Les solutions possibles sont donc (13, 26) après arrondi, car x doit être entier.

Exercice 6 – problème de géométrie dans un repère orthonormé.

a) Déterminer les coordonnées des points A’, B’ et C’, milieux respectifs des segments [BC], [AC], et [AB].

Pour calculer les coordonnées des milieux, on utilise la formule : 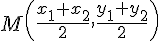$M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$ .

Pour A’: $A'( \frac{-5+7}{2}, \frac{-5-1}{2} ) = A'(1, -3)$ .

Pour B’: $B'( \frac{1+7}{2}, \frac{7-1}{2} ) = B'(4, 3)$ .

Pour C’: $C'( \frac{1-5}{2}, \frac{7-5}{2} ) = C'(-2, 1)$ .

b) Déterminer l’équation réduite des droites (AA’) et (BB’).

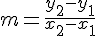
La pente d’une droite passant par deux points $(x_1, y_1)$ et $(x_2, y_2)$ est donnée par : $m=\frac{y_2-y_1}{x_2-x_1}$ .

Pour (AA’): 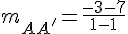$m_{AA'}=\frac{-3-7}{1-1}$ = indefini donc x = 1 (droite verticale).

Pour (BB’): $m_{BB'} = \frac{3+5}{4+5} = \frac{8}{9}$ .

L’équation est donc : 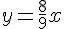$y=\frac{8}{9}x$ .

c) Déterminer les coordonnées de leur point d’intersection K.

En trouvant l’intersection de x = 1 et 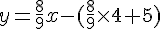$y=\frac{8}{9}x-(\frac{8}{9}\times 4+5)$ (à évaluer), on calcule y.

d) Montrer par le calcul que K appartient à la droite (CC’).

Vérifier que les coordonnées K satisfont à l’équation de (CC’).

e) Quel théorème classique de géométrie aurait permis de démontrer le résultat précédent ?

Le théorème de Thalès.

f) Montrer que K est situé aux deux-tiers des segments [AA’], [BB’], et [CC’] en partant des points A, B, et C.

Vérification des distances par la section 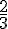$\frac{2}{3}$ .

2) Calculer les distances OA, OB, et OC.

Que peut-on en déduire pour le point O ?

Utiliser la formule de la distance : 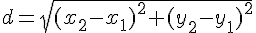$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Comparer les distances entre O et les points A, B, et C.

3) a) Soit A_1(4; -2). Montrer que A, H et A_1 sont alignés.

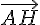
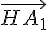
Vérifier le colinéaire des vecteurs $\vec{AH}$ et $\vec{HA_1}$ .

b) Soit C_1(-1; -3). Montrer que C, H et C_1 sont alignés.

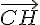
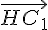
Vérifier le colinéaire des vecteurs $\vec{CH}$ et $\vec{HC_1}$ .

c) Montrer que les triangles AA_1Cet CC_1A sont des triangles rectangles.

Utiliser le théorème de Pythagore pour montrer que certains angles sont droits.

d) Que peut-on en déduire pour le point H ?

Analyser la position de H en lien avec les triangles rectangles.

4) Montrer que les points O, K, et H sont alignés.

Utiliser la colinéarité des vecteurs pour démontrer l’alignement.

Exercice 7 – déterminer les coordonnées des points et intersection.

1) Représentation :

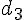
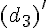
Les droites $d_{3}$ et $(d_{3})^{\prime}$ ont pour équations respectives et .
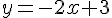
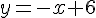
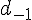
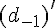
Les droites $d_{-1}$ et $(d_{-1})^{\prime}$ se représentent par les équations et .

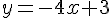
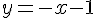
2) Condition de parallélisme :

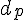
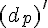
Les droites $d_{p}$ et $(d_{p})^{\prime}$ seront parallèles si leurs coefficients directeurs sont égaux. Donc :

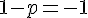
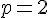
3) Intersection pour 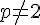$p\neq2$ :

Les coordonnées du point d’intersection 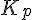$K_{p}$ se trouvent en résolvant :

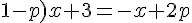
En isolant :

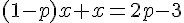
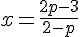
$x=\frac{2p-3}{2-p}$

Puis en remplaçant dans l’équation de $d_{p}$ pour obtenir .

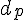
4) Calcul des coordonnées de 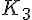$K_{3}$ et $K_{-1}$ :

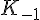
Pour :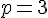

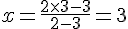
$x=\frac{2\times 3-3}{2-3}=3$

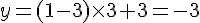
$y=(1-3)\times 3+3=-3$

Pour :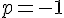

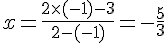
$x=\frac{2\times (-1)-3}{2-(-1)}=-\frac{5}{3}$

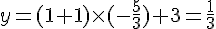
$y=(1+1)\times (-\frac{5}{3})+3=\frac{1}{3}$

Exercice 8 – déterminer l’équation de la droite.

a) Déterminer l’équation de la droite (AB) :

Les points A(1, -2) et B(-3, 1) ont pour coordonnées :

A(1, -2) et B(-3, 1)

Pour trouver l’équation de la droite passant par ces deux points, nous calculons d’abord le coefficient directeur :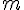

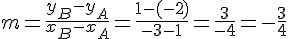
$m=\frac{y_{B}-y_{A}}{x_{B}-x_{A}}=\frac{1-(-2)}{-3-1}=\frac{3}{-4}=-\frac{3}{4}$

L’équation de la droite sous la forme 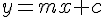est donnée par :

Utilisons le point A(1, -2) pour trouver :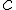

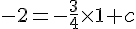
$-2=-\frac{3}{4}\times 1+c$

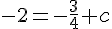
$-2=-\frac{3}{4}+c$

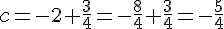
$c=-2+\frac{3}{4}=-\frac{8}{4}+\frac{3}{4}=-\frac{5}{4}$

L’équation de la droite (AB) est donc :

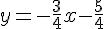
$y=-\frac{3}{4}x-\frac{5}{4}$

b) Pour chaque point, vérifier s’il appartient à la droite (AB) :

C(10; -8,75)

Substituons x = 10 dans l’équation de la droite :

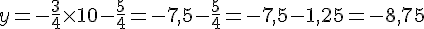
$y=-\frac{3}{4}\times 10-\frac{5}{4}=-7,5-\frac{5}{4}=-7,5-1,25=-8,75$

Donc, le point C appartient à la droite (AB).

D(-20; 13,5)

Substituons x = -20 dans l’équation de la droite :

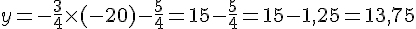
$y=-\frac{3}{4}\times (-20)-\frac{5}{4}=15-\frac{5}{4}=15-1,25=13,75$

Donc, le point D n’appartient pas à la droite (AB).

E(41; -32)

Substituons x = 41 dans l’équation de la droite :

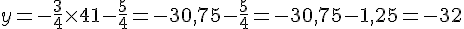
$y=-\frac{3}{4}\times 41-\frac{5}{4}=-30,75-\frac{5}{4}=-30,75-1,25=-32$

Donc, le point E appartient à la droite (AB).

Exercice 9 – nature d’un triangle et équations de droites.

a) Les droites (AB), (AC), (BC) sont-elles parallèles à l’un des axes ?

Pour qu’une droite soit parallèle à l’un des axes, sa pente doit être 0 (parallèle à l’axe des x) ou non définie (parallèle à l’axe des y).

– (AB) : Les points A(-3 ; 2) et B(2 ; 2) ont la même ordonnée, donc la droite (AB) est parallèle à l’axe des x.

– (AC) et (BC) n’ont ni ordonnées ni abscisses identiques donc elles ne sont pas parallèles à l’un des axes.

b) Déterminer les équations de (AB), (AC) et (BC).

– Pour (AB) :

Les points A(-3 ; 2) et B(2 ; 2) donne une pente de 0.

L’équation de (AB) est donc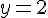

– Pour (AC) :

Les points A(-3 ; 2) et C(2 ; -2) ont une pente 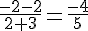$\frac{-2-2}{2+3}=\frac{-4}{5}$

L’équation : 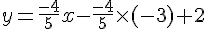$y=\frac{-4}{5}x-\frac{-4}{5}\times (-3)+2$

Donc, 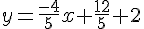$y=\frac{-4}{5}x+\frac{12}{5}+2$

Après simplification : 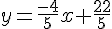$y=\frac{-4}{5}x+\frac{22}{5}$

– Pour (BC) :

Les points B(2 ; 2) et C(2 ; -2) ont la même abscisse, donc (BC) est une droite verticale.

L’équation de (BC) est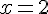

c) Quelle est la nature du triangle ABC ?

– Calculons les longueurs :

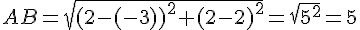
$AB=\sqrt{(2-(-3))^2+(2-2)^2}=\sqrt{5^2}=5$

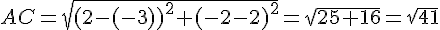
$AC=\sqrt{(2-(-3))^2+(-2-2)^2}=\sqrt{25+16}=\sqrt{41}$

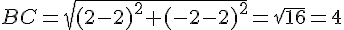
$BC=\sqrt{(2-2)^2+(-2-2)^2}=\sqrt{16}=4$

– Les longueurs ne correspondent pas à un triangle rectangle (par le théorème de Pythagore) et elles sont toutes différentes, donc le triangle ABC est scalène.

Exercice 10 – systèmes et équations de droites.

a) Justifier que l’équation de la droite (AB) est de la forme y = mx + p .

Pour trouver l’équation d’une droite passant par deux points, on utilise la forme y = mx + p .

Les points A(-2;1) et B(2;2) donnent deux relations qui permettent de déterminer m et p .

b) Expliquer pourquoi déterminer m et p revient à résoudre le système :

Le système d’équations est obtenu en substituant les coordonnées des points A et B dans l’équation de y = mx + p :

$\{\begin{array}{l} 1 = -2m + p \\ 2 = 2m + p \end{array}.$

c) Résoudre ce système et donner l’équation de la droite (AB).

Soustrayons la première équation de la deuxième pour éliminer p :

$2 - 1 = (2m + p) - (-2m + p)$

$1 = 4m$

$m = \frac{1}{4}$

Substituons m dans la première équation :

$1 = -2(\frac{1}{4}) + p$

$p = 1 + \frac{1}{2}$

$p = \frac{3}{2}$

Donc, l’équation de la droite (AB) est $y = \frac{1}{4}x + \frac{3}{2}$

d) Déterminer l’équation de la droite (CD).

Pour les points C(21;6) et D(21;2) :

La pente m est $m = \frac{2 - 6}{21 - 21} = \text{indefinie}$

Cela indique une droite verticale : x = 21 .

e) Killian affirme : « Le point E(21;7) est aligné avec A et B mais aussi avec C et D ».

Qu’en pensez-vous ?

Pour que le point E soit aligné avec A et B, il doit vérifier l’équation $y = \frac{1}{4}x + \frac{3}{2}$ .
Vérifions :

$7 = \frac{1}{4}\times 21 + \frac{3}{2}$

$7 = \frac{21}{4} + \frac{3}{2}$

$7 = \frac{21}{4} + \frac{6}{4}$

$7 = \frac{27}{4} \neq 7$

Donc, E n’est pas aligné avec A et B .

E serait aligné avec C et D si x = 21 ce qui est le cas.

Donc, E est aligné avec C et D , mais pas avec A et B.

4.7/5 - (34319 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les équations de droites : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.

D'autres cours et exercices corrigés

Vecteurs

Probabilités

Repérage dans le plan

L’étude de fonction

Les équations et inéquations

Algorithmes et programmes

Inéquations

Simulation et échantillonnage

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 357 917 cours et exercices de maths téléchargés en PDF et 4 250 exercices.