Intervalles et valeur absolue : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Dans cet article, nous allons aborder les intervalles et la valeur absolue, deux concepts fondamentaux en mathématiques pour les élèves de seconde. Comprendre ces notions est essentiel pour maîtriser les compétences en analyse et en géométrie, ainsi que pour résoudre des exercices complexes. Grâce à nos corrections détaillées, vous serez en mesure d’améliorer votre compréhension et votre pratique de ces enjeux mathématiques clé.
Exercice 1 – compléter le tableau suivant.
Pour l’inégalité 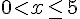
Intervalle : ![x\in]0;5]](https://maths-pdf.fr/latex-images/95fff03bab495e7167ced55d253906ad.png)
Pour l’inégalité 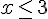
Intervalle : ![x\in]-\infty;3]](https://maths-pdf.fr/latex-images/7d8c65ff8d44e25ee2517929c375c603.png)
Pour l’inégalité 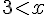
Intervalle : ![x\in]3;+\infty[](https://maths-pdf.fr/latex-images/aa625c6ed88ceba446e46f8af5ab42e1.png)
Exercice 2 – compléter avec appartient ou n’appartient pas.
1. ![2\in]1;3[](https://maths-pdf.fr/latex-images/5e3a31d2224d6921ba71aa85640d1df6.png)
2. ![0\in[-1;2]](https://maths-pdf.fr/latex-images/850d95f337fc0dff9279b2b48de45e12.png)
3. ![\frac{1}{3}\in]0;3[](https://maths-pdf.fr/latex-images/0de3436bf2fa1b3e023148a68bb95e0c.png)
4. ![2\notin]-2;2[](https://maths-pdf.fr/latex-images/10345cc9c8046aebb53b253589c23efd.png)
5. ![\sqrt{2}\notin[-3;1]](https://maths-pdf.fr/latex-images/afd1d0be4cf25f25cce2c10c89a74400.png)
6. ![0\notin]0;+\infty[](https://maths-pdf.fr/latex-images/2df51ded4fc6d4dc01303da3603fe988.png)
7. ![-100\in]-\infty;1]](https://maths-pdf.fr/latex-images/f52008b99bb6358a9c7e0b735b4d8f42.png)
8. 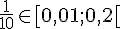
Exercice 3 – compléter les intervalles.
1. ![x\in[7;20]\Left\rightarrow7x\in[49;140]](https://maths-pdf.fr/latex-images/af045f1c0a5ab92b1fcd81d93eba8c6e.png)
2. ![x\in[-1;3]\Left\rightarrow7-x\in[4;8]](https://maths-pdf.fr/latex-images/909a5ba1698481c911ce1a61761d7815.png)
3. ![x\in[-5;7]\Left\rightarrow2x+3\in[-7;17]](https://maths-pdf.fr/latex-images/4913c836dd35d671eb798213ca47d3b3.png)
4. ![x\in[-\infty;-2]\Left\rightarrow-2x\in[1;+\infty[](https://maths-pdf.fr/latex-images/23652fe6febe223ddffe74d2bc7e86b5.png)
5. ![x\in[-\infty;3]\Left\rightarrow3-x\in[-\infty;6]](https://maths-pdf.fr/latex-images/68f019f7f8777650c40bd1b35a260f29.png)
6. ![x\in[-2;1]\Left\rightarrow7+2x\in[-1;1]](https://maths-pdf.fr/latex-images/6ee200f1702766b2dffd6c1ec37ece6b.png)
Exercice 4 – représenter graphiquement un intervalle.
1. Représenter graphiquement l’ensemble des points M(x ; y) :
Intervalle sur x : 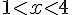
Intervalle sur y :
Représenter ce rectangle sur le plan muni d’un repère orthonormé avec les bornes de x et y définies.
2. Reprendre la question avec l’ensemble des points N(x ; y) :
Équation sur x : 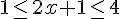
En résolvant l’inéquation :
Équation sur y : 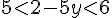
En résolvant l’inéquation : 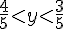
Représentez ces inégalités sur le plan dans un repère orthonormé pour montrer l’espace possible des points N.
Exercice 5 – programme avec Scratch et Python.
1. Que fait ce programme ?
Ce programme vérifie si un nombre 


![\left]a\,;\,b\right[](https://maths-pdf.fr/latex-images/2a3e2632ebf1961a00da17b36c59f05b.png)
2. Modifier ce programme pour qu’il teste si un nombre appartient à l’intervalle ![\left[a\,;\,b\right]](https://maths-pdf.fr/latex-images/4c05d5d4afc02d7fd4dbcb8e3a5b4a1e.png)
![\left]a\,;\,b\right]](https://maths-pdf.fr/latex-images/67ccb8a2af9ce242a35a335c73393d46.png)
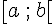
a) Pour vérifier si le nombre appartient à l’intervalle ![\left[a\,;\,b\right]](https://maths-pdf.fr/latex-images/4c05d5d4afc02d7fd4dbcb8e3a5b4a1e.png)
def DansIntervalle(a, b, x):
if a <= x <= b:
return(True)
else:
return(False)
b) Pour vérifier si le nombre appartient à l’intervalle ![\left]a\,;\,b\right]](https://maths-pdf.fr/latex-images/67ccb8a2af9ce242a35a335c73393d46.png)
def DansIntervalle(a, b, x):
if a < x <= b:
return(True)
else:
return(False)
c) Pour vérifier si le nombre appartient à l’intervalle 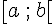
def DansIntervalle(a, b, x):
if a <= x < b:
return(True)
else:
return(False)
Exercice 6 – que fait ce programme ?.
1. Que fait ce programme ? Ce programme teste si le nombre x est strictement supérieur à a. Si c’est le cas, il renvoie VRAI, sinon il renvoie FAUX.
2. Modifier ce programme :
Pour tester si un nombre appartient à l’intervalle 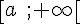
a < x par a \leq x.
Pour tester si un nombre appartient à l’intervalle ![\left]-\infty\;;a\right]](https://maths-pdf.fr/latex-images/0201ba5ae11a5847a6f47838d7515364.png)
a < x par x \leq a.
Pour tester si un nombre appartient à l’intervalle ![\left]-\infty\;;a\right[](https://maths-pdf.fr/latex-images/b149109a03f35addf71076ed5fc21fed.png)
a < x par x < a.
Exercice 7 – ecrire sous forme d’intervalle.
1. 

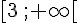
2. 

Réponse simplifiée : ![]-\infty\,;1]\cup]6\,;+\infty[](https://maths-pdf.fr/latex-images/36bccaf098ba0cd36957f1ce28d621ae.png)
3. 

Réponse simplifiée : ![]-\infty\,;2]\cup]5\,;+\infty[](https://maths-pdf.fr/latex-images/d4da644c82d79acf6746cf4e074a8899.png)
4. 

Réponse simplifiée : [3;+\infty[ » alt= »[3;+\infty[ » />
5. 

Réponse simplifiée : 
6. 

Réponse simplifiée : 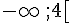
Exercice 8 – intersection d’intervalles.
1.
Les conditions sont 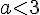
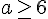
L’ensemble intersection est vide, car il n’y a pas de valeurs de 
2.
Les conditions sont 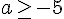
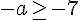
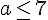
L’ensemble intersection est <span data-mce-type= » bookmark= » » /> » />.
3.
Les conditions sont 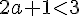
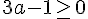
Pour la première : 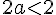
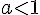
Pour la deuxième : 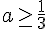
L’ensemble intersection est 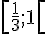
4.
Les conditions sont 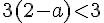
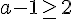
Pour la première : 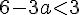
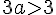

Pour la deuxième : 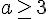
L’ensemble intersection est ![\left]3;+\infty\right[](https://maths-pdf.fr/latex-images/b23d9d47d379f48b62850473b21987a3.png)
Exercice 9 – quels nombres sont égaux à leur valeur absolue ?.
1. 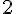
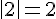
2. 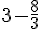
3. 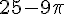
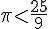
4. 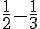
5. 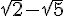
6. 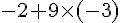
Exercice 10 – donner la valeur absolue.
1.
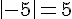
2.
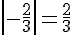
3.
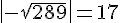
4.
Solution : Calculons l’expression.
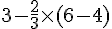
= 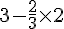
= 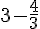
= 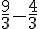
= 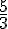
Télécharger ou imprimer cette fiche «intervalles et valeur absolue : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.












