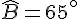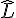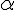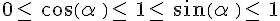Trigonométrie dans le triangle rectangle : cours de maths en 3ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
0.Introduction :
La trigonométrie est un domaine des mathématiques qui traite des relations entre les longueurs et les angles dans un triangle.
Le mot trigonométrie provient du grec trigonos qui signifie « triangulaire » et métron qui signifie « mesure ».
Les origines de la trigonométrie remontent aux civilisations d’Égypte antique, de Mésopotamie et de la vallée de l’Indus vers – 4 000.
2. Formules de trigonométrie dans le triangle rectangle :
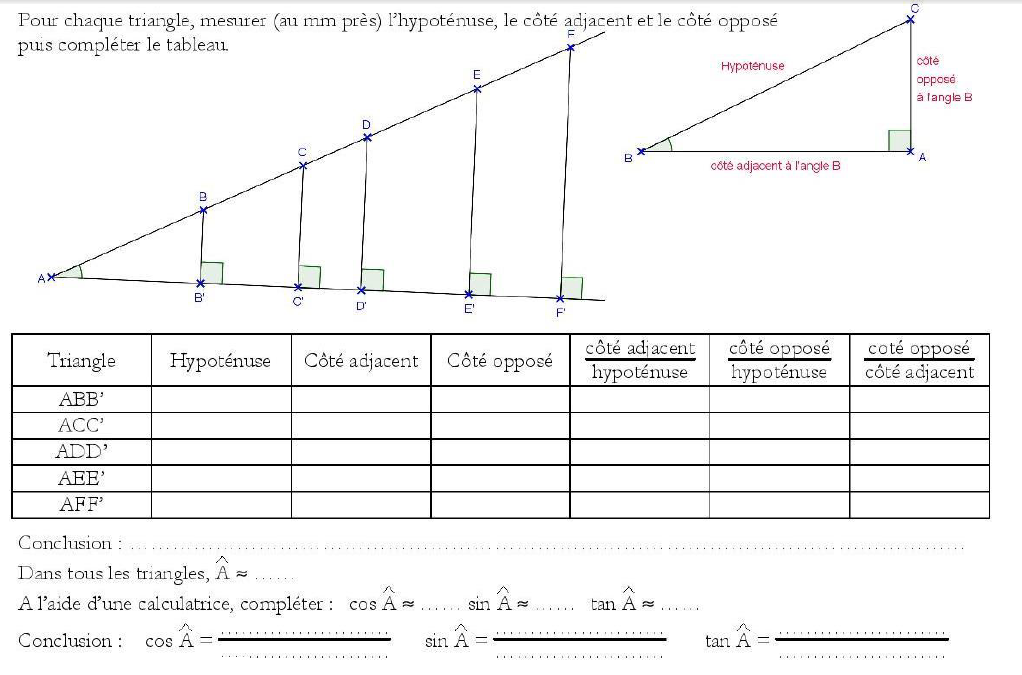
Activité de découverte des formules de trigonométrie :
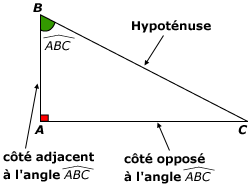
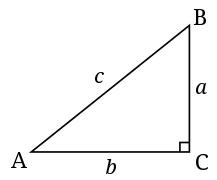
Soit ABC un triangle rectangle en A.
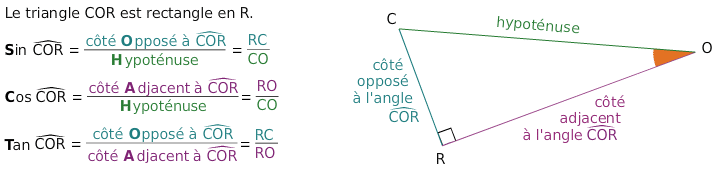
Dans un triangle rectangle, nous avons les formules de trigonométrie suivantes
Moyen mnémotechnique :
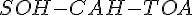
Exemple :
Remarque :
- Pour retenir facilement ces formules, on peut utiliser le moyen mnémotechnique suivant :SOH-CAH-TOA qui correspond aux initiales en gras dans les formules précédentes.
- Le cosinus et le sinus d’un angle aigu sont toujours compris entre 0 et 1.
- La tangente d’un angle aigu est un nombre strictement positif.
Exemple :
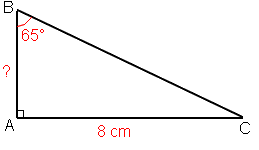
Soit ABC un triangle rectangle en A.
Calculer la valeur de AB arrondie au millimètre.
Dans le triangle ABC rectangle en A :
Je connais :
- AC=8 cm : côté opposé à l’angle
Je cherche :
AB : côté adjacent à l’angle 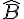
Formule : tangente
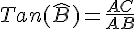
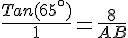
donc
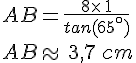
Exemple :
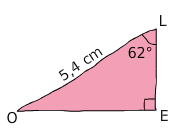
Dans le triangle rectangle LOE, Calculer OE.
On connait :
- l’angle
- la longueur OL (hypoténuse)
On cherche :
la longueur OE (opposé)
Formule :
La seule formule qui fait apparaître les mots « hypoténuse » et « opposé » est le sinus.
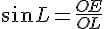
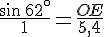
En utilisant la propriété du produit en croix :
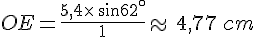
Le cosinus et le sinus sont des quotients de longueurs donc 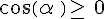
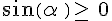
De plus 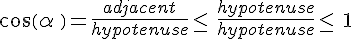
De même, 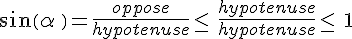
II. Calcul de la mesure d’un angle avec les formules de trigonométrie :
Activité de découverte :
Afin de calculer la mesure d’un angle dans un triangle rectangle ( connaissant son cosinus ou sinus ou tangente), nous utilisons la calculatrice en mode DEGRE (DEG).Les touches qui nous permettent de calculer la mesure de l’angle aigu sont : 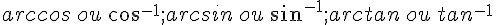
Exemples :
a. Si 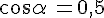
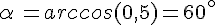
b. Si 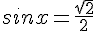
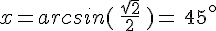
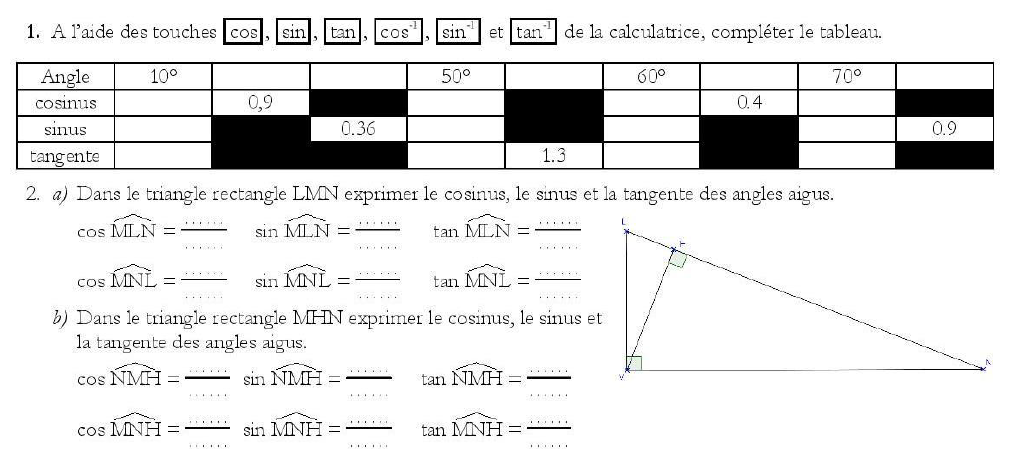
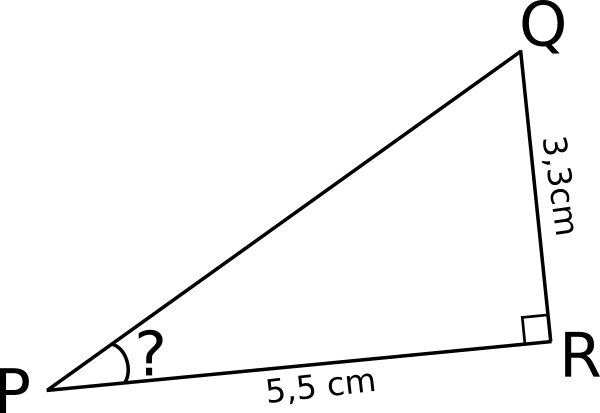
c. Soit PQR un triangle rectangle en R.
Calculer la mesure de l’angle 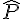
Dans le triangle PQR rectangle en R :
Je connais :
- PR=5,5 cm : côté adjacent à
- QR=3,3 cm : côté opposé à
Je cherche :
Formule : TANGENTE
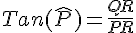
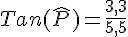
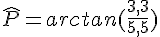
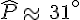
Exemple :
Dans le triangle rectangle FUN, déterminer la mesure de l’angle 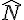
Dans ce triangle rectangle,
on connaît :
- la longueur UN (adjacent);
- la longueur FU (opposé).
La seule formule qui fait apparaître les mots « adjacent » et « opposé » est la tangente.
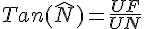
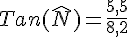
On utilise la calculatrice en mode DEGRE et la touche « arctan ».
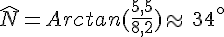
Télécharger ou imprimer cette fiche «trigonométrie dans le triangle rectangle : cours de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 3ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.