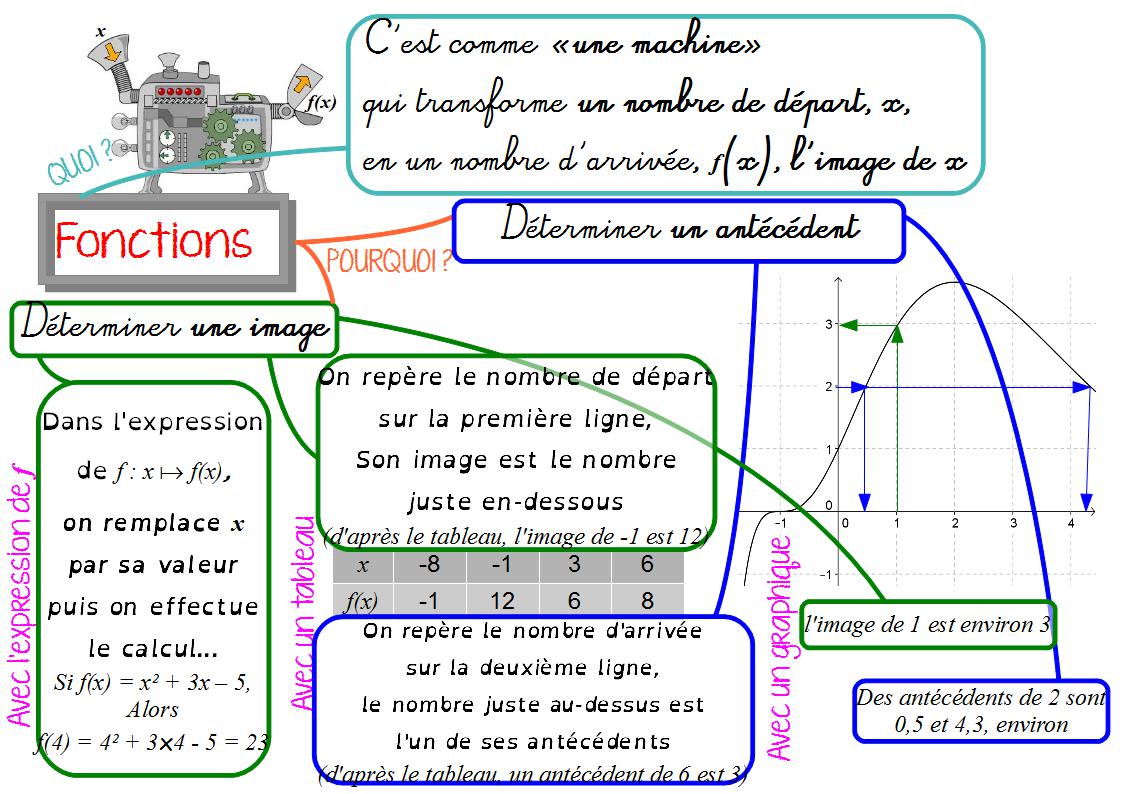
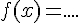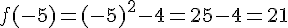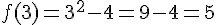Fonctions et généralités : cours de maths en 3ème sur l’image et antécédent à imprimer en PDF.
Mis à jour le 20 décembre 2025
I. Notion de fonction :
1.Activité d’introduction :
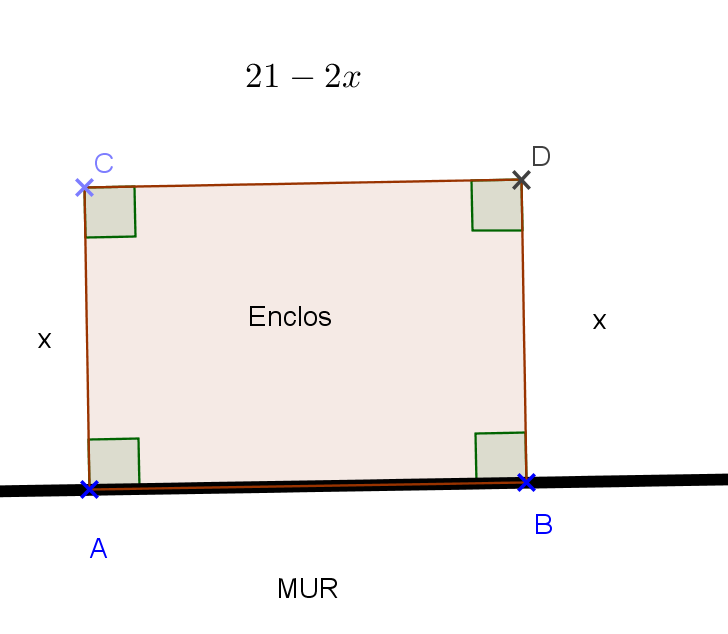
Un propriétaire souhaite construire un enclos rectangulaire le long d’un mur pour son chien de garde.
Il dispose d’un grillage ayant une longueur de 21 mètres.
Il souhaite maximiser l’espace pour son chien et veut utiliser l’intégralité du grillage.
La largeur de l’enclos doit être inférieure à 10,5 mètres.
1.Notons 
Quelle est l’expression de la longueur de l’enclos en fonction de
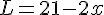
2.Quelle est l’expression développée et réduite de l’aire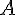 
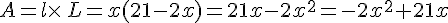
3.Calculer l’aire de l’enclos pour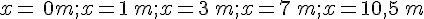 
Pour
.
Pour
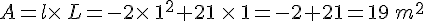
Pour
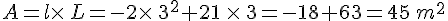
Pour
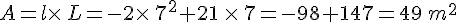
Pour
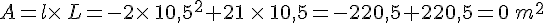
4.On met en place un processus mathématique, noté f, que l’on appelle fonction.
On décide d’associer à chaque largeur x, l’unique aire de l’enclos notée f(x).
Nous avons mis en place la fonction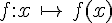 
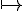
Quelle est l’expression littérale de f ?
Nous avons montré précédemment que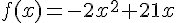 
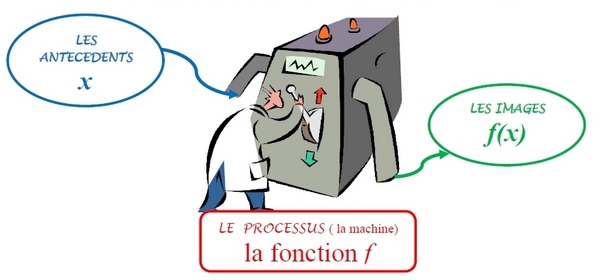
5.Calculer f(7) qui est l’image de 7 par la fonction f.
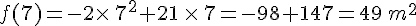
Remarque :
Nous avons déjà calculé cette valeur, en effet lorsque la largeur est de 7 m, l’aire de l’enclos est de 49 m².
6.A l’aide du tableur de votre calculatrice, compléter le tableur de valeurs suivant :
7.Dans le repère suivant, placer tous les points de A à Q puis, tracer la courbe de cette fonction :
Sur l’axe des abscisses, nous placerons les valeurs de x et sur l’axe des ordonnées, nous placerons les valeurs de f(x).
8.Retrouver graphiquement pour quelle valeur de x l’aire de l’enclos est maximale et calculer cette aire.
L’aire de l’enclos est maximale pour x = 5,25 m.
2.Résolution du problème avec Geogebra :
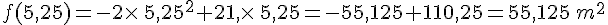
II. Généralités sur les fonctions :
1.Définitions et vocabulaire :
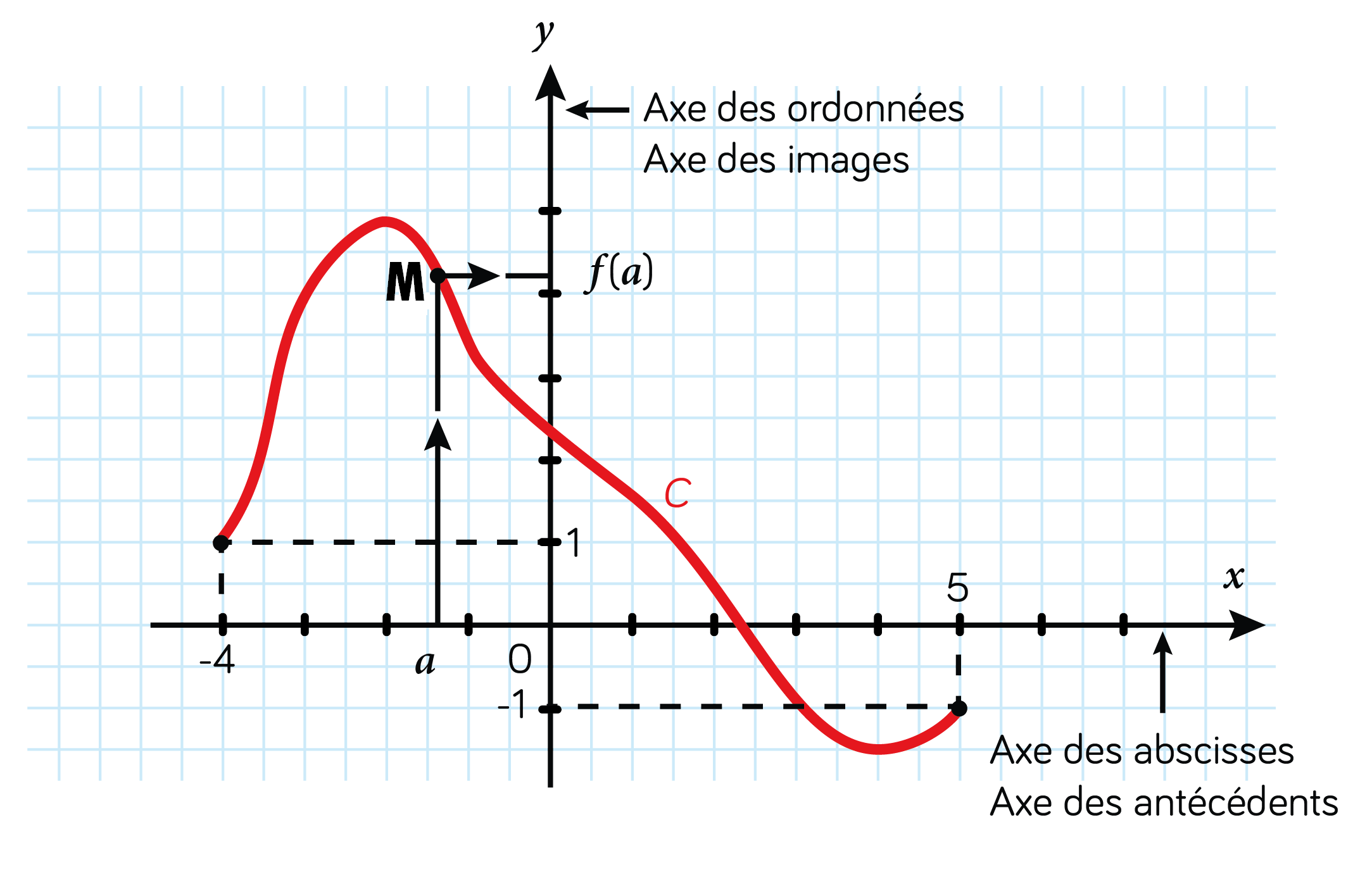
Une fonction, notée f, est un processus mathématique qui à tout nombre x d’un ensemble de départ associe un unique nombre, noté f(x), dans un ensemble d’arrivée.
Le nombre x est appelé l’antécédent de f(x).
Le nombre f(x) est appelé l’image du nombre x par la fonction f.
Une fonction f peut être notée de deux façons :
- la fonction f telle que
- la fonction f définie par
Exemple :
On appelle f la fonction qui, à la longueur du côté d’un carré, associe le périmètre du carré.
La fonction f associe au nombre 5, le nombre 20.
Plus généralement, elle associe au nombre x, le nombre 4x.
On note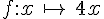 
Remarque :
Pour une fonction f, on utilise la notation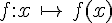
Exemple de fonctions :
La fonction qui associe à un nombre son double est définie par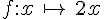 
La fonction triple est la fonction h définie par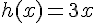 
la fonction k qui a une longueur x associe l’aire du carré est définie par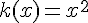 
2.Image et antécédent
remarque :
L’image d’un nombre est unique. Par contre, un nombre peut avoir plusieurs antécédents.
Exemples :
- Soit f la fonction telle f(-2)=0.
- l’image de -2 par f est 0.
- 0 est un antécédent de -2 par f.
2. Soit la fonction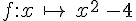 
Cela signifie qu’à tout nombre, ici noté x, la fonction f associe un unique nombre noté f(x).
On dit que l’image du nombre x par la fonction f est le nombre x²-4.
3. Tableau de valeurs
On considère une fonction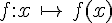
Nous pouvons résumer les images et les antécédents correspondants dans un tableur de valeurs.
Exemple :
Reprenons la fonction f définie par f(x)=x²-4.
Voici un tableau de valeurs de cette fonction :
Sur la première ligne, nous avons les antécédents et sur la seconde, les images.
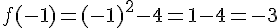
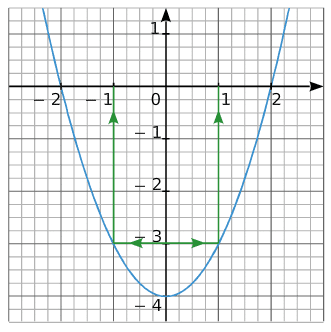
De plus, nous pouvons remarquer que 5 a au moins deux antécédents qui sont x = -3 et x = 3.
4.Courbe représentative d’une fonction :
Soit f une fonction définie sur un ensemble. On appelle courbe représentative d’une fonction f, notée 
Exemple :
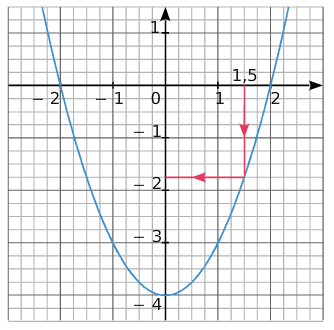
Les courbes ci-dessous représentent la fonction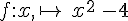 
L’image de 1,5 par la fonction f est – 1,75.
- Les antécédents de -3 sont x=1 et x=-1.
III. Carte mentale sur les fonctions :
Télécharger ou imprimer cette fiche «fonctions et généralités : cours de maths en 3ème sur l'image et antécédent à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 3ème
Exercices de 3ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.
