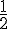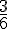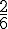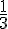Probabilités : cours de maths en 3ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
I. Les probabilités : événements et issues.
1.Définitions et vocabulaire :
Une expérience est dite aléatoire lorsque l’on ne peut pas prévoir avec certitude quel résultats va se produire. Les différents résultats possibles s’appellent les issues.
Un événement est constitué par les différentes issues de l’expérience aléatoire.
Exemple :
Expérience : On lance un dé à six face non pipé.
Les issues possibles sont : 1,2,3,4,5,6.
Un événement peut être : obtenir le 1,2,…6 ou encore obtenir un nombre pair.
Ces événements (obtenir 1, obtenir 2,….obtenir 6) sont appelés événements élémentaires.
Exemple :
- On lance une pièce de monnaie : les issues sont pile ou face.
- On lance l’écoute de morceaux de musiques en mode aléatoire parmi une liste de dix titres. Les issues sont les dix titres de la liste.
- On essaye de deviner à l’avance le vainqueur de la coupe du monde de football parmi les 32 équipes de la phase finale. Les issues sont les trente-deux pays en compétition.
- On lance un dé à jouer comportant six faces. Les issues sont 1,2,3,4,5,6.
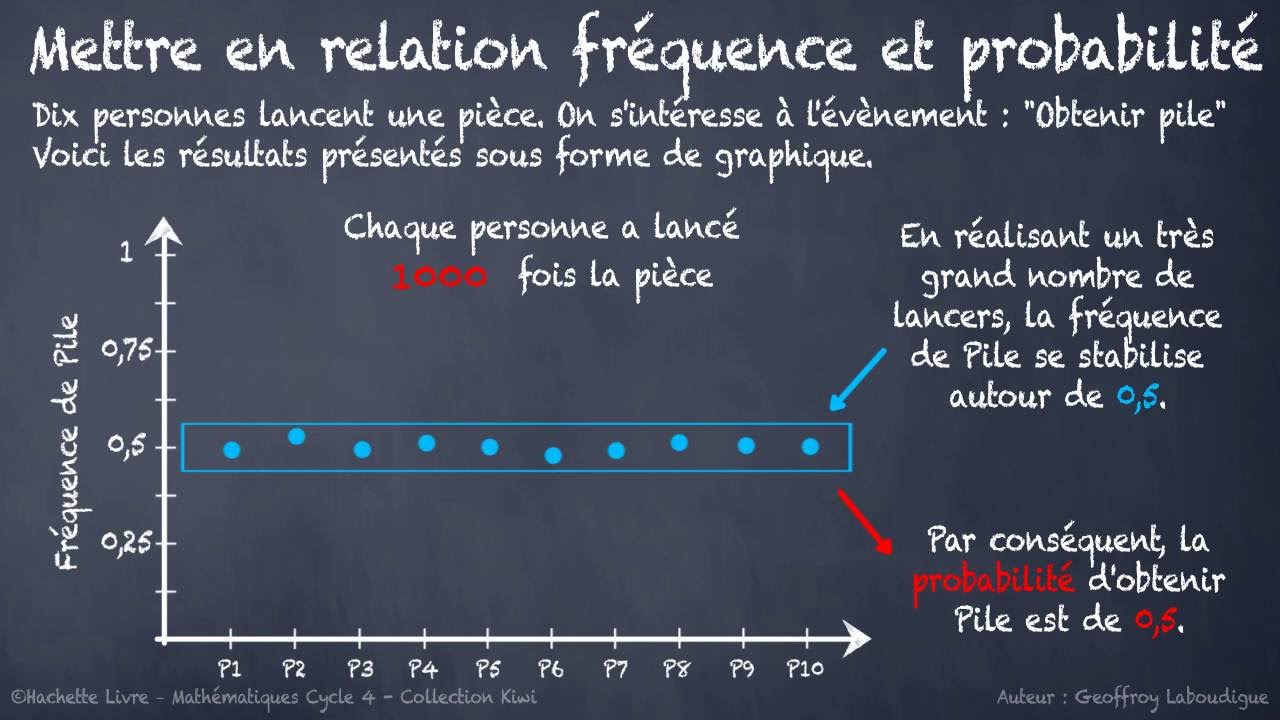
2.Probabilité et fréquence :
de n’importe quel événement de cette expérience finit par se stabiliser et converge vers la probabilité de cet événement.
3.Notion de probabilité :
événement a de se produire. Ce quotient est appelé la probabilité de l’événement.
Soit A un événement, on note P( A ) la probabilité que l’événement A se réalise.
La probabilité d’un événement est égale au quotient :
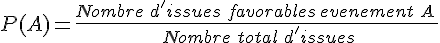
Exemple :
Reprenons l’expérience aléatoire du dé.
Chaque événement élémentaire : obtenir le 1,…, obtenir le 6.
La probabilité de chacun de ces événements est de 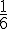
Exemple :
- On lance l’écoute d’un morceau de musique en mode aléatoire parmi une liste de dix titres. « Le morceau joué dure moins de trois minutes » est un événement.
- On essaye de deviner à l’avance le vainqueur de la coupe du monde de football parmi les 32 équipes de la phase finale. « Le pays gagnant est un pays d’Afrique » est un événement. Le pays vainqueur a gagné sa demi-finale est un événement certain.
- On lance un dé à jouer comportant six faces numérotées de 1 à 6. « Le dé tombe sur un nombre pair » est un événement. « Le dé tombe sur le chiffre 9 » est un événement impossible.
Exemple :
Pour le lancer dé dé.
Nous avons 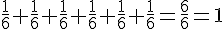
B:<<obtenir un chiffre supérieur à 7>>
Exemple :
- On lance une pièce de monnaie équilibrée. Chaque face a autant de chance d’être obtenue que l’autre. C’est une situation d’équiprobabilité. La probabilité d’obtenir pile est donc de
- On lance un dé à jouer classique à six faces et non truqué. Chaque face a autant de chances de sortir qu’une autre. Sur les six faces du dé, trois faces portent un nombre pair et trois faces portent un nombre impair, donc la probabilité d’obtenir un nombre impair est de
Remarque :
La probabilité d’un événement impossible est de 0 et la probabilité d’un événement certain est de 1.
4. Les issues et arbre de probabilité
- Une expérience est aléatoire lorsque l’on ne peut pas prévoir à l’avance quel va être son résultat parmi les différentes issues possibles.
- La schématisation qui nous permet de visualiser les différentes issues possibles d’une expérience aléatoire s’appelle l’arbre de probabilité.
- Chaque branche de cet arbre de probabilités indique la probabilité d’une issue.
- On dit que l’arbre est pondéré par les probabilités.
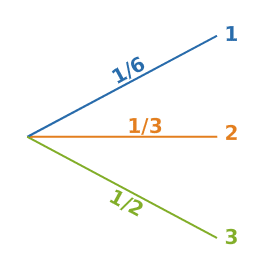
Exemple :
Katia lance un dé équilibré à six faces numérotées 1,2,2,3,3 et 3.
On observe le nombre indiqué sur la face supérieure : les issues sont 1,2 et3.
Le dé est équilibré, donc chaque face a autant de chance de sortir qu’une autre.
- Ainsi, la probabilité de sortie du nombre 1 est de
- Deux faces portent le numéro 2, donc la probabilité de l’issue 2 est
- De même, celle de l’issue 3 est
On résume ces résultats sur l’arbre de probabilité ci-dessous :
II. Les événements certains, incompatibles et contraires :
- Un événement est dit certain si se produit nécessairement.
- La probabilité d’un événement certain est égale à 1.
Exemple :
Un événement certain pour le lancer de dé serait :
A:<<obtenir un chiffre inférieur à 7>> et P(A)=1.
- Un événement est dit impossible si il ne peut pas se produire.
- La probabilité d’un événement incertain est égale à 0.
Exemple :
Un événement incertain pour le lancer de dé serait :
B:<<obtenir un chiffre supérieur à 7>> et P(B)=0.
- Deux événements sont incompatibles s’ils ne peuvent pas se produire en même temps.
- L’événement contraire d’un événement est celui qui se réalise lorsque l’événement n’a pas lieu.
Exemple :
Deux événements incompatibles seraient C : <<obtenir un chiffre pair>> et D : <<obtenir un chiffre impair>>.
Soit A un événement, on note 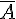
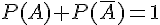
Exemple :
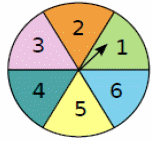
On tourne une roue bien équilibrée.
Notons l’événement A : <<sortie du chiffre 1>> alors 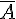
Nous avons 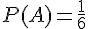
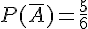
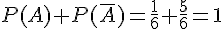
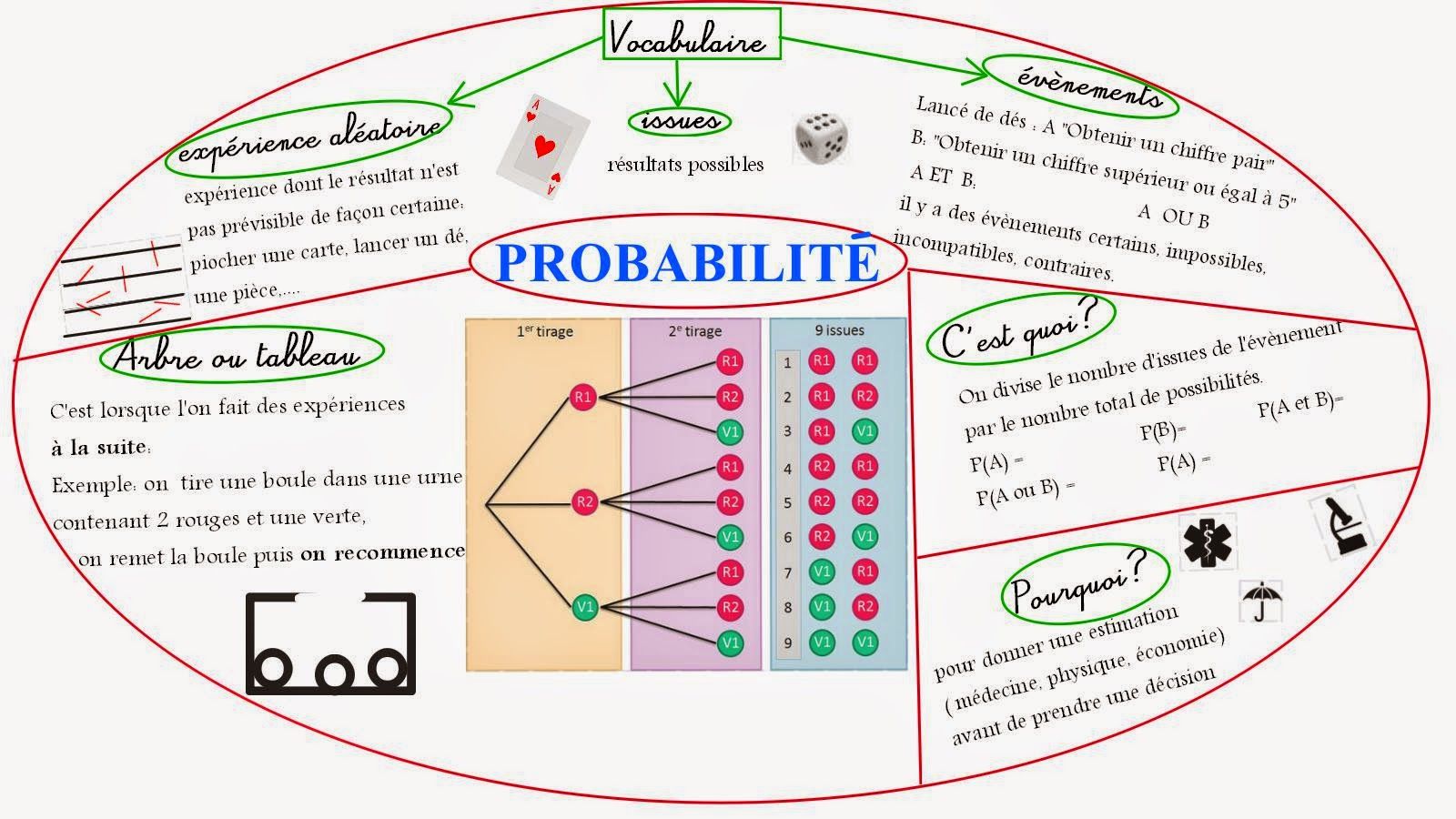
III. Carte mentale sur les probabilités :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «probabilités : cours de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 3ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.