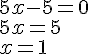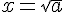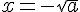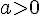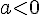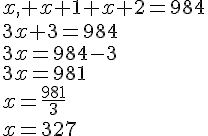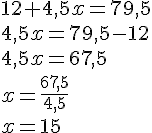Les équations et inéquations : cours de maths en 3ème à imprimer en PDF.
Mis à jour le 4 février 2026
Avant d’aborder cette leçon, il faut avoir acquis le contenu du cours sur les équations de l’année précédente.
I.Les équations du premier degré à une inconnue :
Soient a,b et c trois nombres relatifs tel que 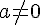
- On appelle équation du premier degré à une inconnue toute égalité qui peut se ramener à cette forme :
- La lettre x est appelée inconnue de l’équation.
- Résoudre une équation, c’est trouver toutes les valeurs de x qui vérifient l’égalité.
- Toute valeur de x qui vérifie l’égalité est appelé solution de l’équation.
- L’expression ax+b est appelée premier membre de l’équation.
- L’expression c est appelée second membre de l’équation.
Soient a et b deux nombres relatifs. La solution de l’équation 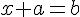
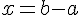
Soient a et b deux nombres relatifs tel que 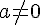
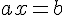
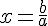
Exemple :
Résoudre l’équation 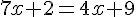
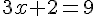
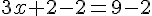
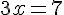
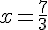
La solution de cette équation est 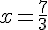
Exemple :
Résoudre l’équation suivante :
II. Les équations-produits :
Un produit de facteurs est nul si et seulement si, un des facteurs, au moins, est nul.
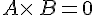
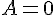
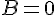
Exemple :
Résoudre l’équation-produit suivante :
Un produit de facteurs est nul si et seulement si, un des facteurs, au moins, est nul.
Par conséquent, nous avons :
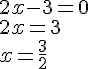
Exemples:
Résoudre les équations suivantes :
1.
Un produit de facteurs est nul si et seulement si l’un des facteurs, au moins, est nul.
Par conséquent :
ou
Les deux solutions de cette équation sont x=3 et x= – 3.
2.
Un produit de facteurs est nul si et seulement si l’un des facteurs, au moins, est nul.
Par conséquent :
ou
Les deux solutions de cette équations sont x = -1 et x = 1.
III.Les équations du type x²=a :
Les solutions de x²=a sont :
- 0 si a = 0;
- ensemble vide si
Exemples :
Résoudre les équations suivantes :
a. 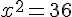
36>0 donc il y a deux solutions qui sont :
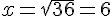
L’ensemble solution est 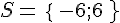
b. 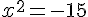
-15<0 donc il y a aucune solution, ou encore, le carré d’un nombre est toujours positif ou nul.
L’ensemble solution est .
IV. Résolution de problèmes et d’équations
Exercice 1 :
Trouver 3 nombres entiers consécutifs dont la somme est égale à 984.
On posera comme inconnue le plus petit nombre.
On note x le plus petit nombre alors :
Les trois nombres recherchés sont 327,328 et 329.
Exercice 2 :
Un club de sport propose la formule suivante : une carte d’adhérent de 12 € puis
l’utilisation de la salle de gymnastique facturée 4,50 € l’heure.
Désignons par x le nombre d’heure d’utilisation de la salle de gymnastique.
Déterminer le prix à payer en fonction du nombre d’heure d’utilisation.
Au bout de combien d’heure d’utilisation le prix à payer est de 79,50 € ?
Nous avons :
Au bout de la quinzième heure, le prix a payer sera de 79,50 euros.
Exercice 3 :
Le réservoir d’une voiture est plein au un tiers. On rajoute 42 litres pour le remplir.
Quelle est sa contenance ?
On choisira comme inconnue la contenance totale du réservoir.
Soit x la contenance en litre de ce réservoir.
Ce réservoir a une contenance de 63 litres.
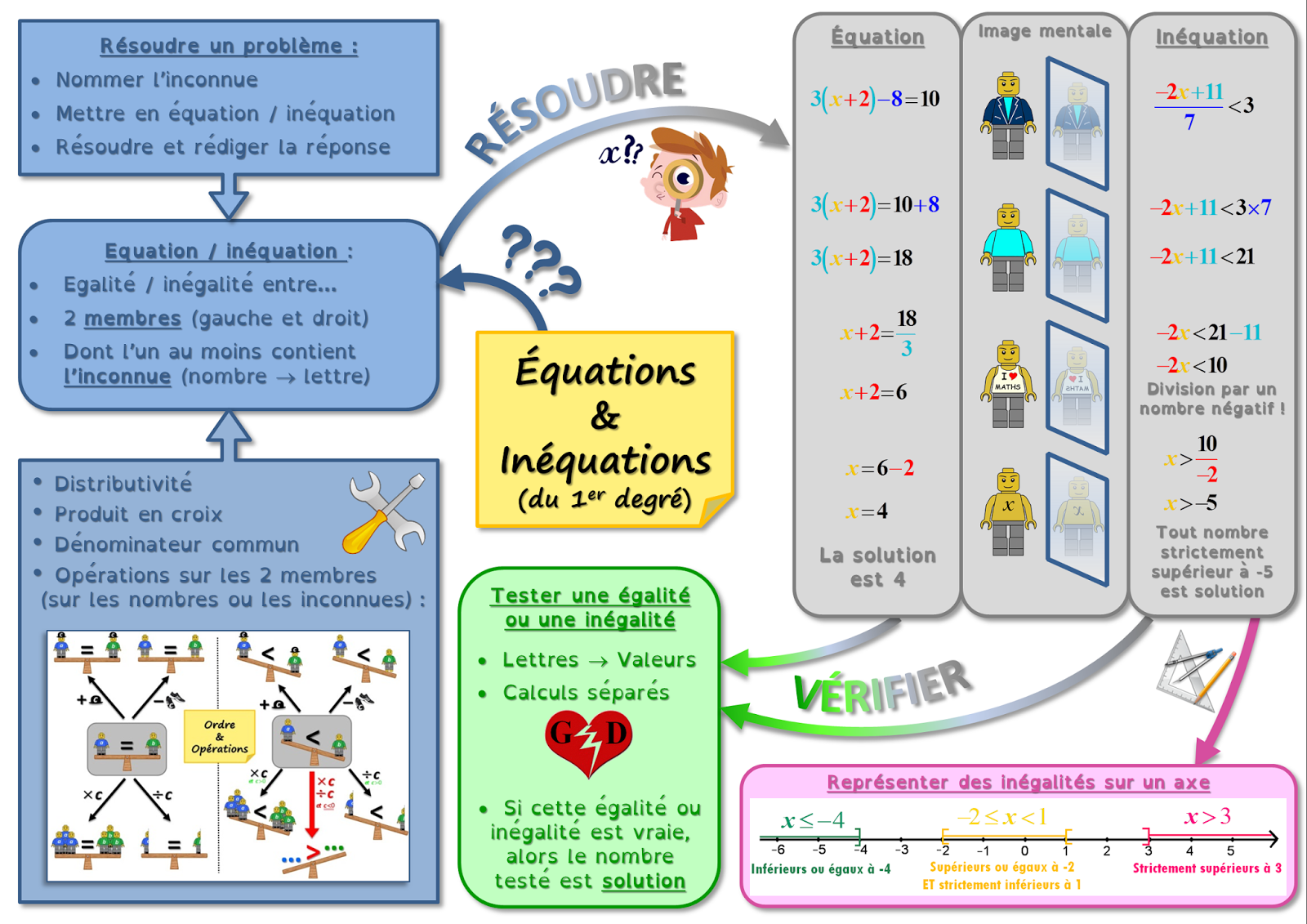
V.Carte mentale sur les équations et inéquations :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «les équations et inéquations : cours de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 3ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.

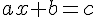
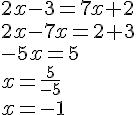
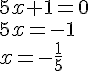
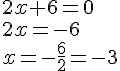
![(x+1)(2x-7)+(x+1)(3x+2)=0\\(x+1)[(2x-7)\,+(3x+2)]=0\\(x+1)(5x-5)=0](https://maths-pdf.fr/latex-images/9b5240b770291efc699788777eae585b.png)