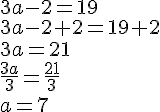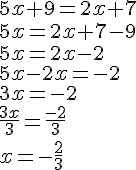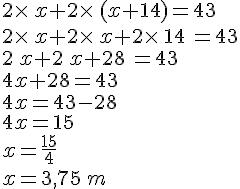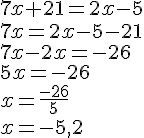Les équations et les problèmes : cours de maths en 4ème à imprimer en PDF.
Mis à jour le 29 janvier 2026
Les équations du premier degré à une inconnue avec un cours de maths en 4ème qui vous donnera la possibilité d’apprendre les définitions et les propriétés de ce chapitre. L’élève devra avoir les compétences de résoudre une équation en utilisant les propriétés de transformations et de transpositions qui permettent de modifier les égalités sans en changer l’ensemble solution. Un autre objectif de cette leçon sera de résoudre des problèmes de la vie courante en quatrième.
I. Les équations du premier degré à une inconnue :
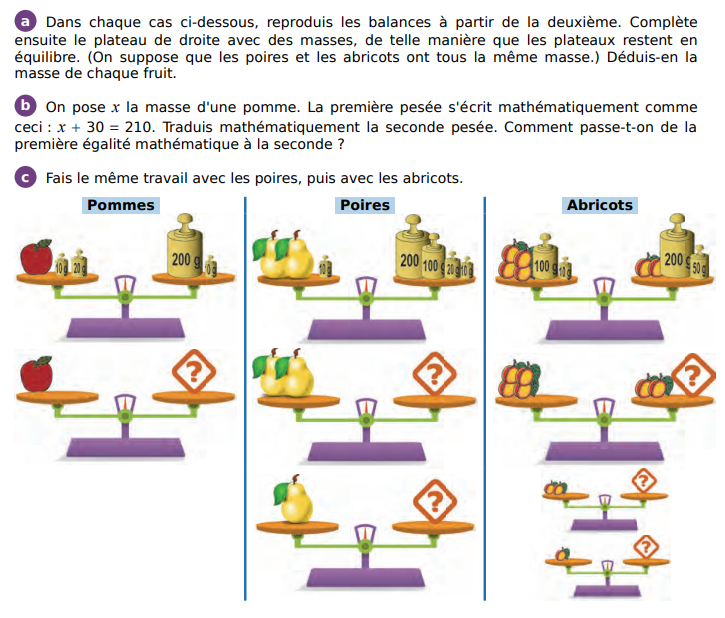
1.Activité d’introduction aux équations :
2.Définitions et vocabulaire :
On considère quatre nombres relatifs a,b,c et d.
- On appelle équation du premier degré à une inconnue, toute égalité du type :
(avec
- La lettre
- Résoudre une équation, c’est trouver toutes les valeurs de x qui vérifient l’égalité.
- Si elles existent, chacune de ces valeurs est appelée solution de l’équation.
- L’expression littérale située à gauche du signe = s’appelle le premier membre et celle située à droite s’appelle le second membre de l’équation.
Exemples :
Voici quelques équations :
3. Résolution d’équations du type x+a=b :
Soient a et b deux nombres relatifs. L’équation 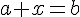
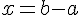
Exemple :
Résoudre les équations.
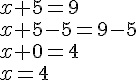
Exemple :
Résoudre l’équation 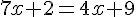
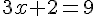
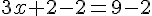
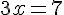
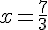
La solution de cette équation est 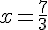
4. Résolution d’équations du type ax=b (avec a non nul) :
Soient a et b deux nombres relatifs tel que 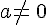
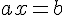
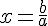
Exemple :
1.Résoudre les équations.
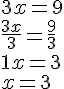
2. Résoudre :
II. Résolution de problèmes:
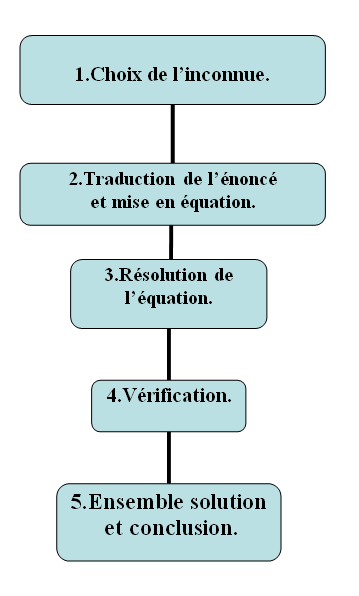
1.Méthodologie :
2.Exemples de problèmes :
Voici les différentes étapes de résolution de problèmes du premier degré ç une inconnue :
3) Résolution de l’équation
4) Vérification
5) Conclusion
a. Le périmètre de ce rectangle est de 43 mètres, calculer la valeur de 
Soit 
Nous avons :
b.
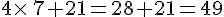
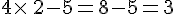
Les résultats ne sont pas égaux. Par conséquent, Jules et Julie n’ont pas pu entrer le nombre 4.
Notons 
Jules a saisi : 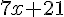
Julie a saisi : 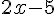
Nous obtenons l’équation :
Conclusion : Julie et Jules ont saisi le nombre – 5,2.
Applications :
Problème 1 :
Une balance à deux plateaux est en équilibre lorsque l’on place 10 cubes et une masse de 2 kg sur l’un des plateaux et 2 cubes et une masse de 30 kg sur l’autre. Quelle est la masse d’un cube?
Problème 2 :
Un père a 30 ans et son fils a 10 ans.
Dans combien d’années l’âge du père sera-t-il le double de celui du fils?
Problème 3 :
L’eau de Javel est utilisée diluée. Une solution diluée à 2% contient 2 cl d’eau de Javel et 98 cl d’eau pour former un litre (100 cl) de solution. Une solution diluée à 30% contient 30 cl d’eau de Javel pour former un litre (100 cl) de solution.
Quelle quantité de solution à 30% faut-il ajouter à 1 litre d’une solution à 2 % pour obtenir une solution à 10 %?
Problème 4 :
Un arbre haut de 10 m et un poteau haut de 2 m sont situés en face l’un de l’autre sur chacune des rives d’une rivière large de 30 m. Au sommet de chacun d’eux est perché un oiseau. Ils se lancent tous deux à la même vitesse et au même instant sur une pauvre mouche qui les nargue à la surface de l’eau. Par un effet magique de Dame Nature, ils l’atteignent au même moment et se fracassent le bec dans un contact plus que vigoureux, et de ce fait se retrouvent bredouilles.
A quelle distance du pied de l’arbre se trouvait cette mouche miraculée?
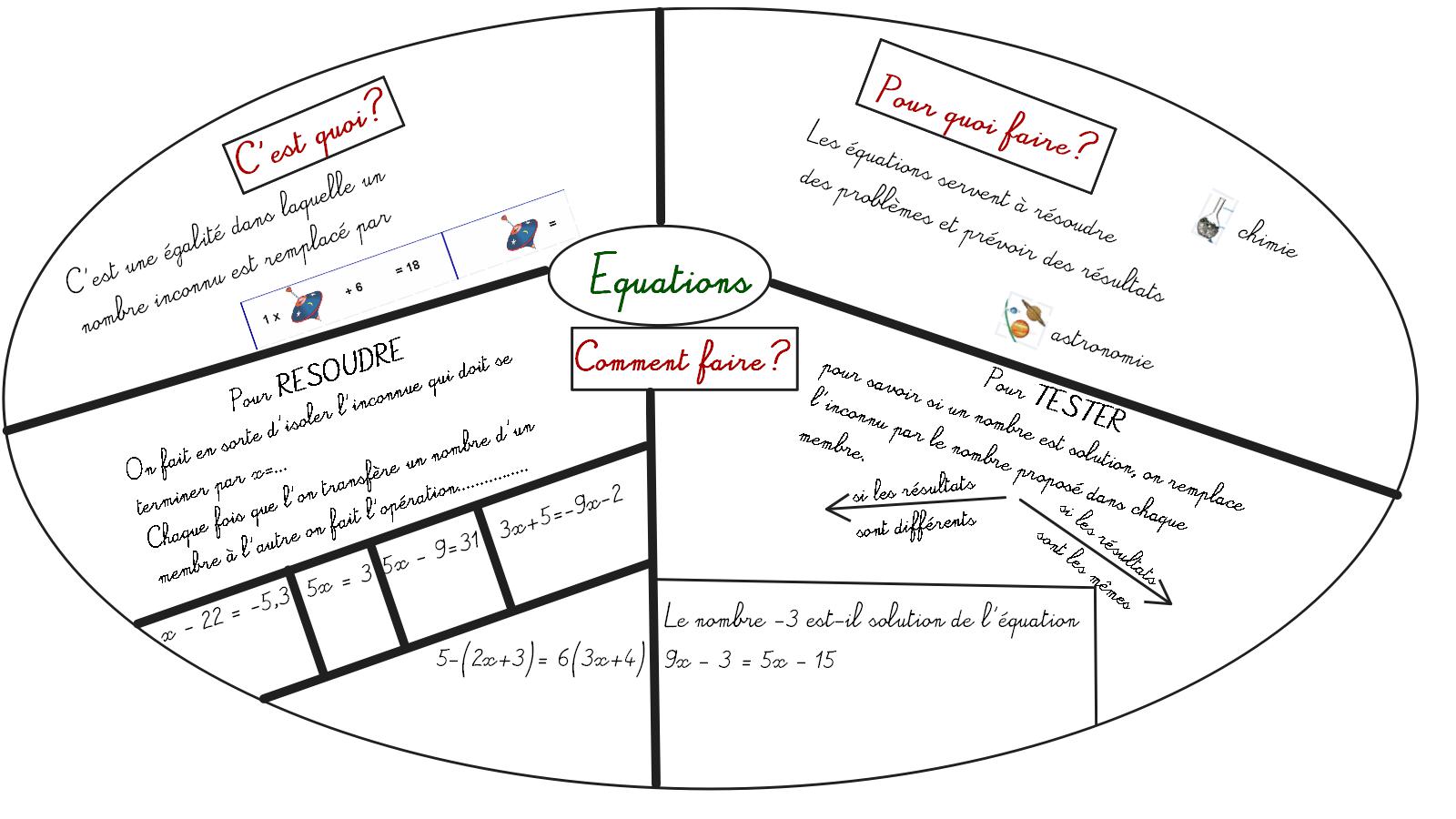
III. Carte mentale sur les équations :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «les équations et les problèmes : cours de maths en 4ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Exercices de 4ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.