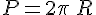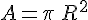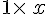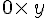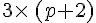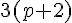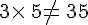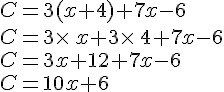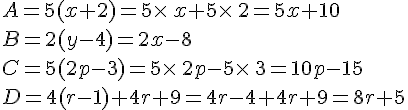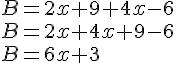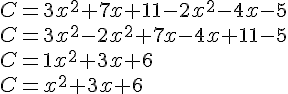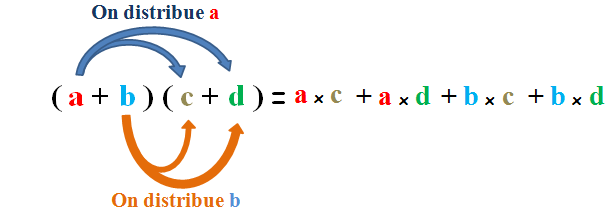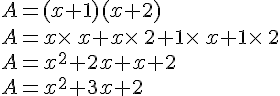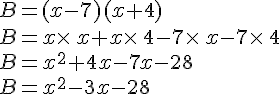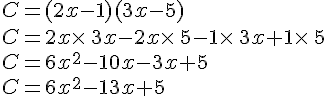Calcul littéral et double distributivité : cours de maths en 4ème à imprimer en PDF.
Mis à jour le 27 janvier 2026
Le calcul littéral à travers un cours de maths en 4ème qui vous permettra d’assimiler les définitions et les propriétés du calcul algébrique. L’élève devra être capable de réduire une expression et de savoir développer en utilisant les propriétés de simple ou double distributivité en quatrième. Calculer la valeur d’une expression en substituant une valeur pour la variable étudiée.
Avant d’aborder cette leçon, il faut avoir acquis le cours sur le calcul littéral de l’année précédente.
I. Le calcul littéral : rappels de 5ème.
1.Définitions et vocabulaire.
Exemples :
- L’aire d’un carré de côté c s’exprime avec l’expression littérale
- Un rectangle de longueur L et de largeur l a un périmètre qui s’exprime avec l’expression littérale
.
Exemples :
- Pour un rectangle de longueur L et de largeur l , son périmètre vaut
.
- Un cercle de rayon R a pour périmètre
Remarque :
- On peut simplifier
- L’expression
- Attention : on ne peut pas supprimer le signe x entre deux nombres
On considère un nombre relatif a.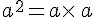
et se lit a au cube.
Exemples :
Aire d’un carré de côté a est 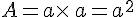
Le volume d’un cube de côté a est
2. Evaluer une expression littérale
Exemples :
Considérons l’expression littérale 
- Si x=3 alors
- Si x = -2 alors
On dit que l’on substitue (remplace) la valeur de x.
On passe, ainsi, du calcul littéral au calcul numérique.
3. La simple distributivité du calcul littéral
Exemples :
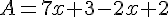
Exemples :
sont des formes factorisées.
Exemples :
Réduire les expressions suivantes :
Preuve :
Exemples :
Développer et réduire des expressions :
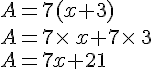
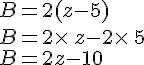
Exemples :
En utilisant la simple distributivité, développer les expressions littérales suivantes :
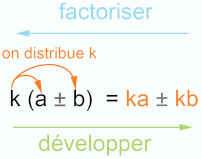
- Développer une expression littérale, c’est l’écrire comme somme de termes.
- Factoriser une expression littérale, c’est l’écrire comme produit de facteurs.
Exemples :
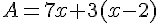
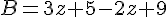
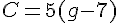
est une forme factorisée.
Exemples :
Réduire les expressions littérales suivantes :
L’expression 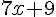
II. La double distributivité :
Exemples :
Développer et réduire les expressions suivantes :
Exemples :
Développer et réduire les expressions littérales suivantes :
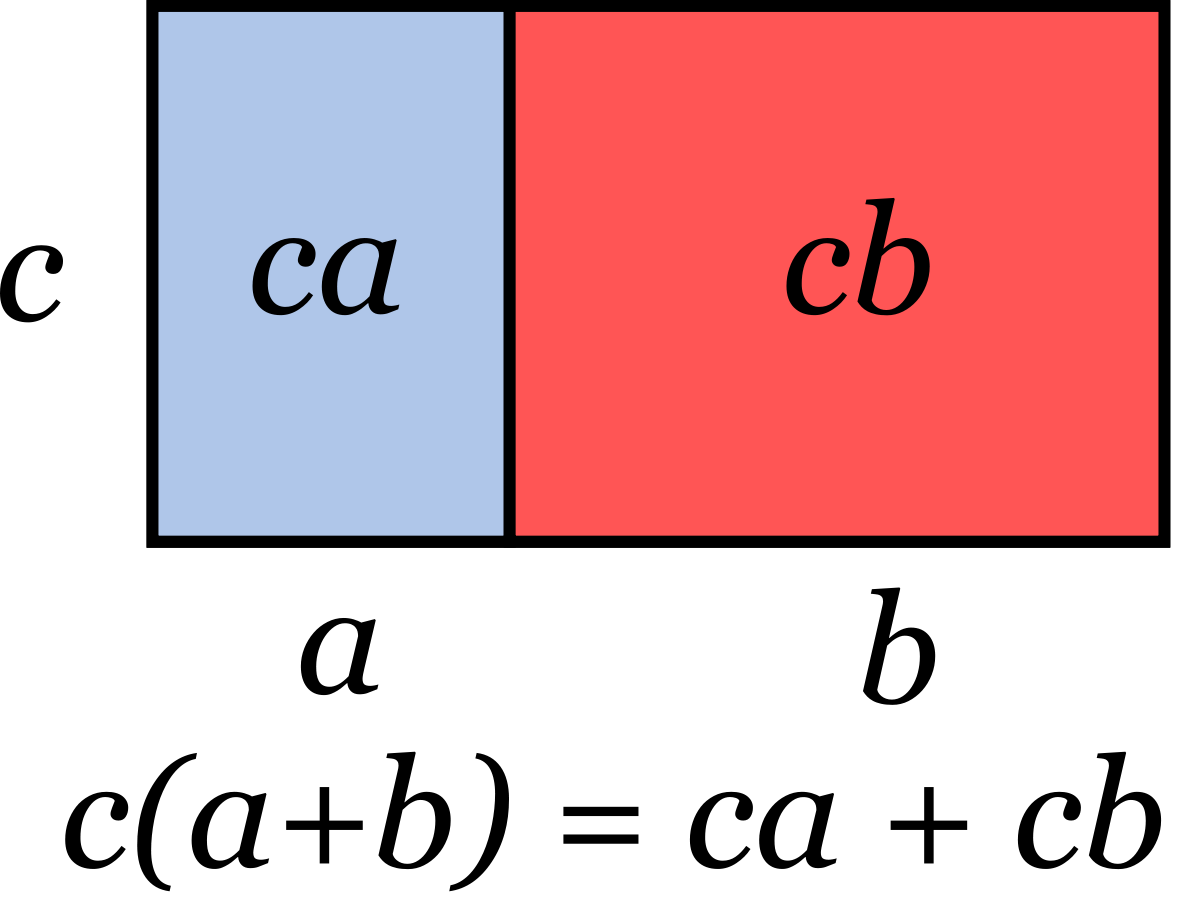
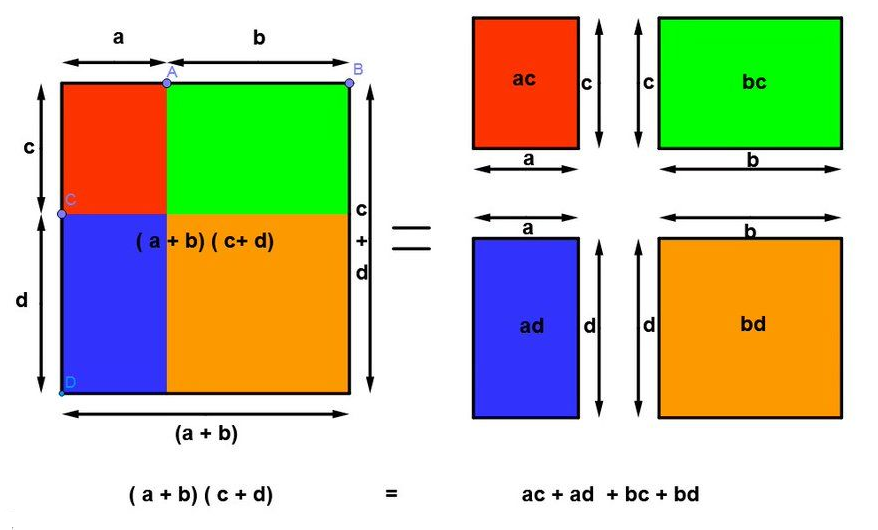
III. La double distributivité à l’aide de la géométrie :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «calcul littéral et double distributivité : cours de maths en 4ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 4ème
Exercices de 4ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.