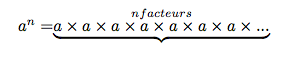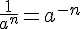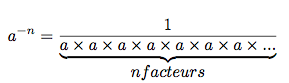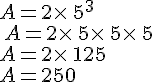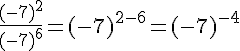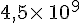Puissances de 10 et d’un nombre relatif : cours de maths en 4ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
Lors des années précédentes, vous avez abordé certaines puissances, notamment celles de 2 et 3
Exemple :
se lit 5 au carré.
se lit 2 au cube.
I.Les puissances d’un nombre relatif :
1.Cas où l’exposant est positif :
Pour tout entier positif 
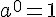
n est appelé l’exposant.
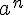
Remarque:
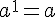
Exemples :
2.Cas où l’exposant est négatif :
Exemples :
Remarque :
En l’absence de parenthèses, les puissances sont prioritaires par rapport aux quatre opérations.
Exemple :
Calculer.
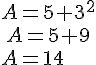
3.Produit de puissances :
On considère 
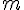

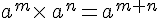
Preuve :
=
=
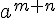
m fois n fois (m+n) fois
Exemples :
Calculer les produits de puissances.
4.Puissance de puissances :
On considère 
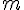

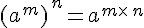
Exemples :
Calculer les expressions numériques.
5.Quotient de puissances :
On considère 
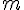

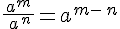
Preuve :
Exemples :
Calculer les quotients.
Remarque :
Nous avons dit au début de la leçon que 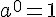
Nous allons expliquer d’où provient cette formule.
mais, nous avons aussi
.
Par conséquent, 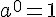
II. Cas particuliers : les puissances de 10.
1.Formules et puissances de 10 :
Nous retrouvons les mêmes formules en prenant 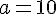
(n fois)
(inverse d’une puissance)
(puissance de puissance)
(produit de puissances)
(quotient de puissances)
Exemples :
Effectuer les calculs.
Exemples :
Calculer la valeur des expressions suivantes :
2.L’écriture (ou notation) scientifique d’un nombre :
On considère x un nombre relatif.
Il existe un entier relatif non nul a et un entier 
avec
.
Cette écriture est appelée écriture scientifique ( ou notation scientifique) du nombre a .
Exemples :
Donner l’écriture scientifique des nombres suivants :
Exemples :
- Age de la terre : 4 500 000 000 années =
- Rayon d’un atome : 0,000 000 000 529 m =
m.
aPPLICATIONS :
1.Un vaisseau spatial a mis 20 ans pour faire le voyage planète X-Terre. Sachant que la planète X est située à 4,5 années-lumière de la Terre et qu’une année-lumière est égale à km, calculer la vitesse moyenne de ce vaisseau spatial exprimée en km par an.Donner l’écriture scientifique du résultat.
2. Ecrire le nombre suivant sous la forme du produit d’un entier par une puissance de 10, puis sans utiliser de puissance de 10 :
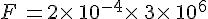
3. 170 000 milliards de milliards de milliards est un ordre de grandeur du nombre de manières de jouer les dix premiers coups d’une partie d’échec. Ecrire ce nombre en notation scientifique.
4. Donner un ordre de grandeur du nombre de petits déjeuners pris par un homme pendant toute sa vie sachant que la durée moyenne de vie est de 77 ans.
5. Une année-lumière est la distance parcourue par la lumière pendant une année. La vitesse de la lumière est 300 000 km/s. Donner un ordre de grandeur d’une année-lumière.
3. Règles de priorités
Exemples :
4.Vocabulaire
Exemples :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «puissances de 10 et d'un nombre relatif : cours de maths en 4ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 4ème
Exercices de 4ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.