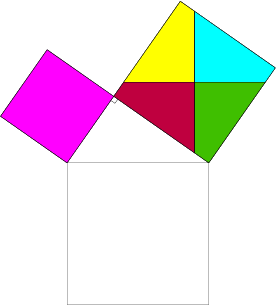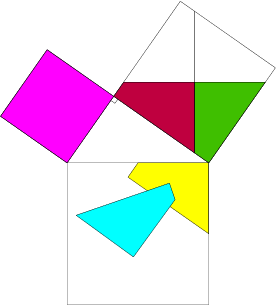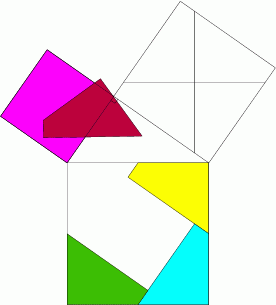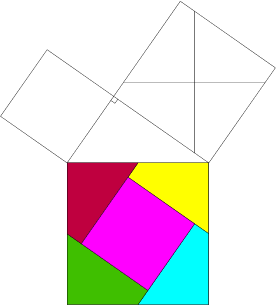
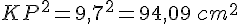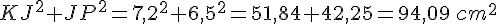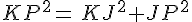Théorème de Pythagore : cours de maths en 4ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
Le fameux théorème de Pythagore à travers un cours de maths en 4ème complet qui vous permettra d’assimiler la partie directe et réciproque. L’élève devra être capable de donner l’égalité de Pythagore dans un triangle rectangle et de calculer la valeur d’une troisième longueur. Réciproquement, il devra être capable d’affirmer si un triangle possède un angle droit connaissant la valeur des trois longueurs en quatrième.
Il était pluridisciplinaire, il s’intéressait à la philosophie, aux mathématiques, aux sciences et à l’astronomie.
Il participa aux jeux olympiques à l’âge de 17 ans et remporta toutes les épreuves du pugilat (ancêtre de la boxe).
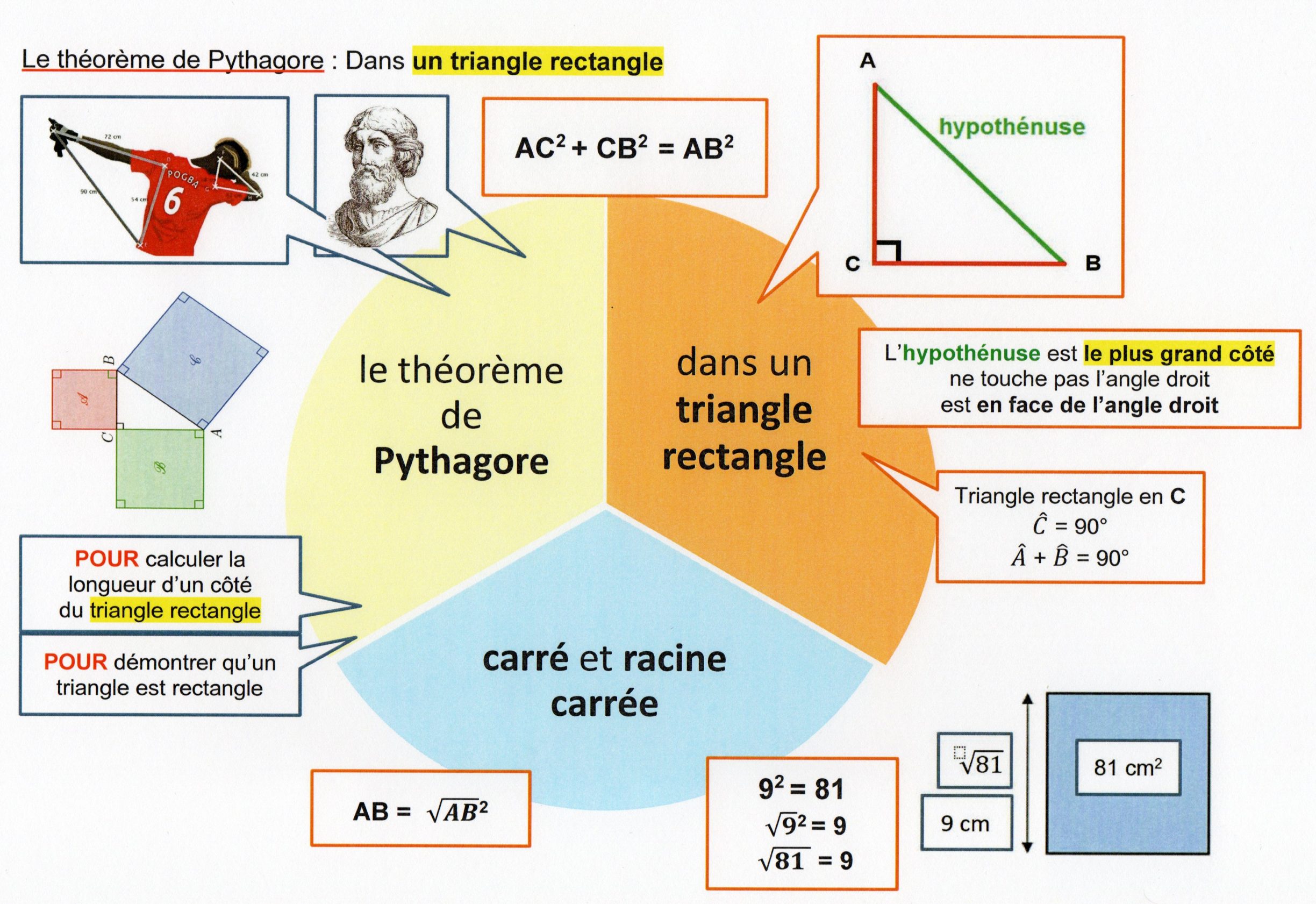
0. Vocabulaire du triangle rectangle
- Un triangle rectangle est un triangle qui possède un angle droit;
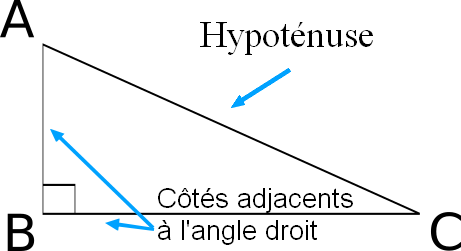
- Le coté le plus long d’un triangle rectangle, qui est le côté opposé à l’angle droit, s’appelle l’hypoténuse.
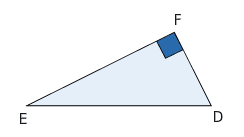
Exemple :
- DEF est un triangle rectangle en F;
- [ED] est l’hypoténuse : c’est le plus long côté du triangle rectangle;
- Les deux côtés adjacents à l’angle droit sont [FD] et [FE], ils sont perpendiculaires.
3.Partie directe du théorème de Pythagore :
On dit que «le carré de l’hypoténuse est égal à la somme des carrés des côtés adjacents à l’angle droit».
Remarque :
Exemples :
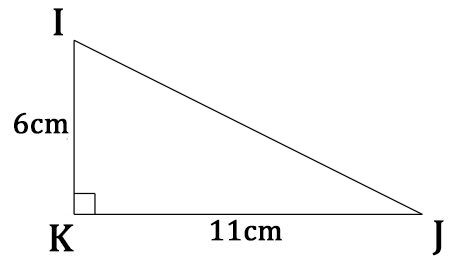
1.Soit un triangle rectangle IKJ rectangle en K tel que KI=6 cm et KJ = 11 cm.
Calculer la valeur de IJ. Arrondir le résultat au dixième.
Le triangle KIJ est rectangle en K.
Je peux appliquer la partie directe du théorème de Pythagore :
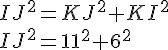
Les puissances sont prioritaires car elles contiennent des multiplications.
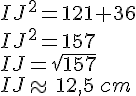
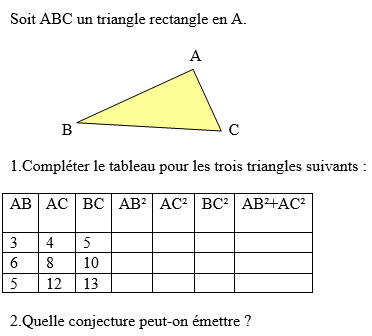
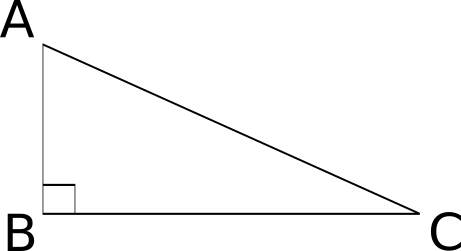
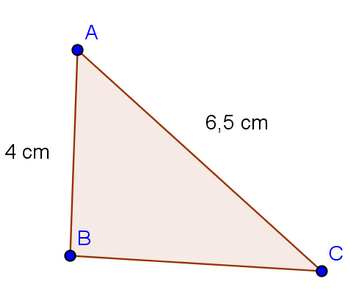
2.Soit un triangle rectangle ABC rectangle en B tel que AC=6,5 cm et AB = 4 cm.
Calculer la valeur de BC. Arrondir le résultat au dixième.
Le triangle ABC est rectangle en B.
Je peux appliquer la partie directe du théorème:
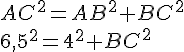
Exemple :
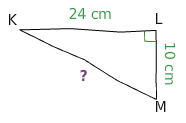
Soit KLM un triangle rectangle en L tel que KL = 24 cm, LM = 10 cm.
Calculer KM.
Le triangle KLM est rectangle en L donc d’après la partie directe du théorème de Pythagore, nous avons l’égalité suivante :
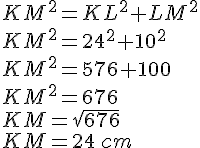
Exemple :
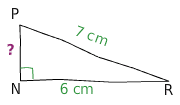
Soit NPR un triangle rectangle rectangle en N tel que PR = 7 cm et Nr = 6 cm.
Calculer NP (arrondir le résultat au dixième).
Le triangle PNR est rectangle donc d’après la partie directe du théorème de Pythagore,
nous avons l’égalité suivante :
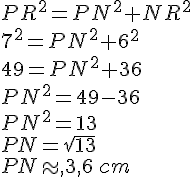
Application :
Une chèvre C est attachée à un piquet P planté au coin d’un pré carré de 15 m de côté.
Quelle doit être, approximativement, la longueur de la corde pour que la chèvre puisse brouter tout le pré?
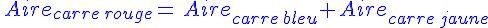
Remarque :
II. Réciproque du théorème de Pythagore :
Si 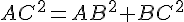
Remarque :
Exemple :
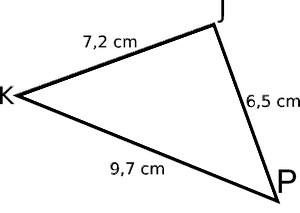
Soit KJP un triangle tel que KJ = 7,2 cm, JP = 6,5 cm et KP = 9,7 cm.
Ce triangle est-il rectangle ?
- Le côté le plus long est [KP].
- Calculons séparément :
et
- Nous avons
Exemple :
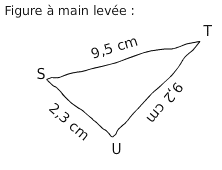
Soit STU un triangle rectangle en U tel que ST = 9,5 cm; Su = 2,3 cm et UT = 9,2 cm.
Le plus grand côté est [ST].
Je calcule séparément :
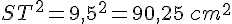
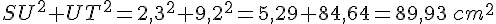
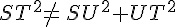
Exemple :
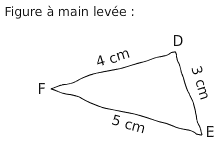
Soit DEF un triangle tel que FD = 4 cm; FE = 5 cm et DE = 3 cm.
Le côté le plus long est [FE].
Je calcule séparément :
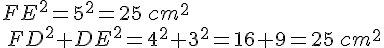
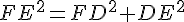
Télécharger ou imprimer cette fiche «théorème de Pythagore : cours de maths en 4ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 4ème
Exercices de 4ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.