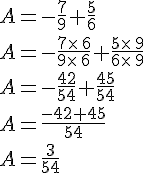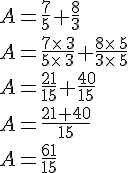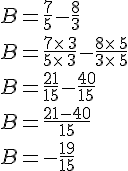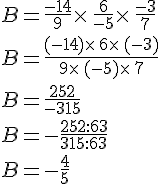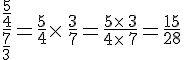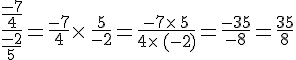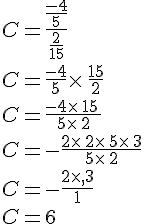Fractions : cours de maths en 4ème à imprimer en PDF.
Mis à jour le 27 janvier 2026
Les fractions avec un cours de maths en 4ème qui vous permettra d’assimiler les notions de ce chapitre. L’élève devra savoir réduire deux fractions au même dénominateur et effectuer des calculs en utilisant les quatre opérations addition, soustraction, multiplication et division). Être capable de comparer ou de ranger dans l’ordre croissant ou décroissant deux fractions mais également, savoir les placer sur une droite graduée. Un des autres objectifs de cette leçon sera de résoudre des problèmes de la vie courante en quatrième.
I. Addition et soustraction:
1. Cas où le dénominateur est le même :
Pour additionner (ou soustraire) deux fractions ayant le même dénominateur, il faut :
- conserver le dénominateur en commun;
- additionner ( ou soustraire) les numérateurs.
On considère a,b et c trois nombres relatifs tels que 
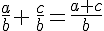
Exemples :
Calculer.
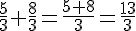
Exemples :
Calculer 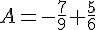
- On cherche un multiple commun aux dénominateurs 9 et 6.
Les premiers multiples de 9 non nuls sont : 9, 18, 27 …
Les premiers multiples de 6 non nuls sont : 6, 12, 18, 24 …
On constate que 18 est un multiple commun à 9 et à 6.
- On cherche le nombre égal à et le nombre égal à qui ont pour
dénominateur 18 :
2. Cas où le dénominateur est différent :
Pour additionner (ou soustraire) deux fractions n’ayant pas le même dénominateur, il faut :
- réduire ces fractions au même dénominateur;
- appliquer la règle précédente.
On considère a, b, c et d quatre nombres relatifs tels que 
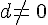
et
Exemple :
Calculer
II. Multiplication de fractions :
Pour effectuer le produit de deux fractions, il faut :
- multiplier les numérateurs entre eux;
- multiplier les dénominateurs entre eux.
On considère quatre nombres relatifs a, b, c et d tels que 
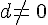
.
Exemples :
Calculer
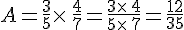
Exemples :
Calculer 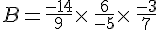
- On détermine d’abord le signe du résultat en utilisant la règle des signes.
Ici, les trois facteurs sont négatifs, donc le produit est négatif.
- On multiplie les numérateurs entre eux et les dénominateurs entre eux
- Pour finir, on simplifie le résultat :
III. Division:
L’inverse de

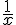
Diviser par un nombre non nul, c’est multiplier par son inverse.
On considère a, b, c et d quatre nombres relatifs avec 
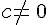
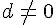
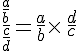
Exemples :
Diviser par 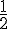
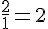
Exemples :
Calculer 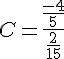
- On détermine l’inverse du dénominateur en «permutant» le
numérateur et le dénominateur.
Ici l’inverse de est 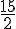
- On multiplie la dernière fraction obtenue avec la fraction qui est au
numérateur :
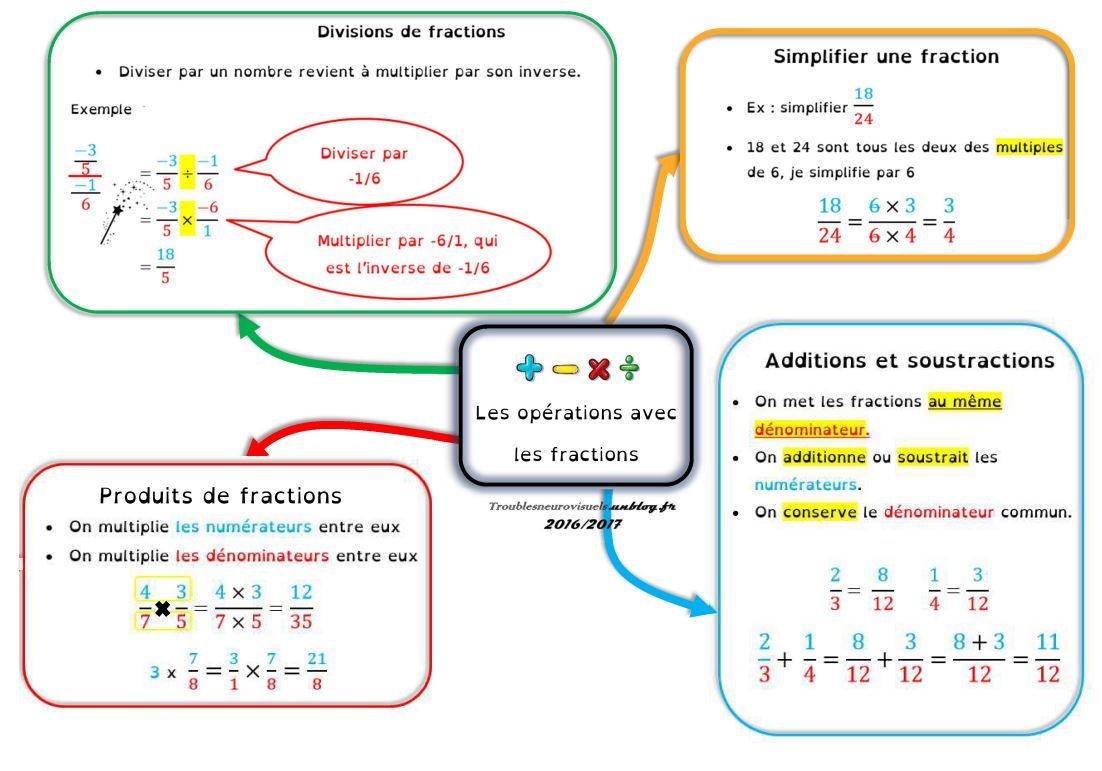
IV. Carte mentale sur les fractions :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «fractions : cours de maths en 4ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 4ème
Exercices de 4ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.