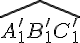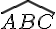Translation et rotation : cours de maths en 4ème à imprimer en PDF.
Mis à jour le 1 février 2026
I. La translation :
Effectuer la translation d’une figure 
- une direction (deux sens);
- un sens;
- une longueur.
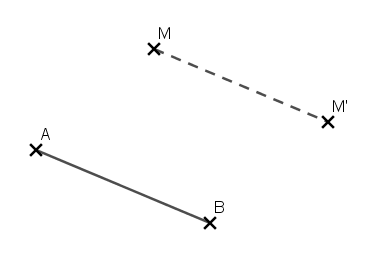
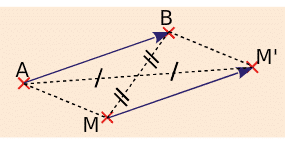
Soit M un point et AB une longueur.
- on note M’ le translaté du point M par la translation qui transforme le point A en B.
- on dit que M’ est l’image du point M par la translation qui transforme A en B.
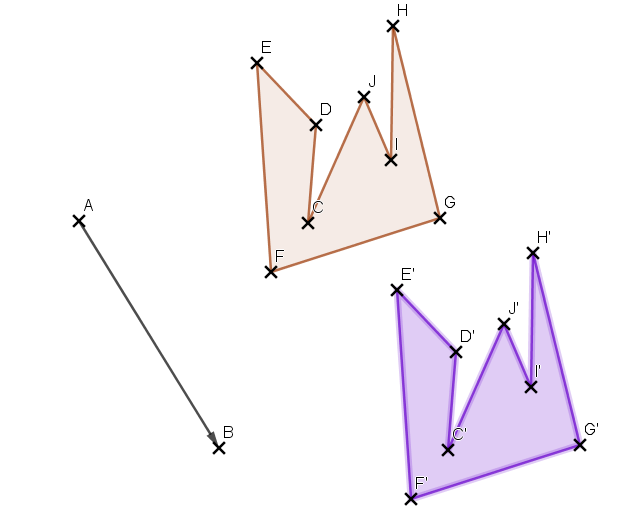
Exemples :
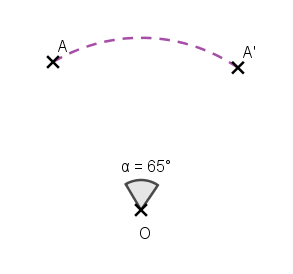
La figure violette est l’image de la figure rouge par la translation qui transforme le point A en B.
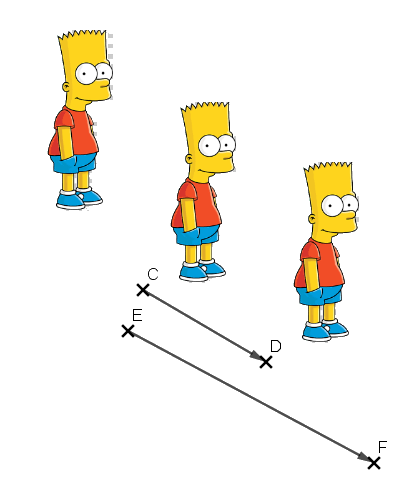
Ci-dessous, nous avons deux translations de Bart Simpson.
La translation qui transforme C en D puis, la translation qui transforme E en F.
Elle conserve toutes les propriétés géométriques d’une figure:
- les longueurs, les périmètres et les aires de figures;
- les mesures d’angles;
- l’alignement, le parallélisme et l’orthogonalité, etc…
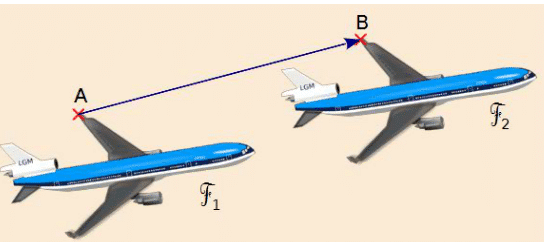
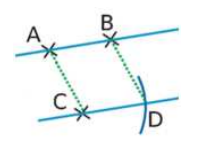
Soit la translation qui transforme A en B.
Notons D l’image de C par cette translation.
Le quadrilatère ABDC est un parallélogramme.
II. La rotation :
Effectuer la rotation d’une figure 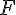
- un angle
- un sens ( horaire ou anti-horaire).
Soit M un point et 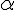
- on note M’ l’image du point M par la rotation d’angle
Remarque :
L’image du centre O par une rotation de centre O et d’angle 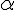
Exemples :
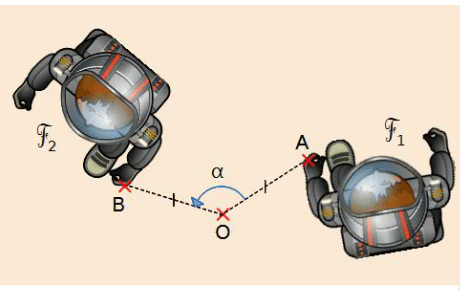
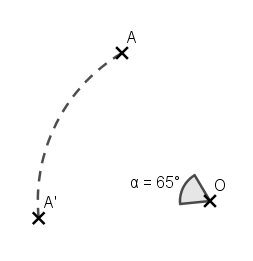
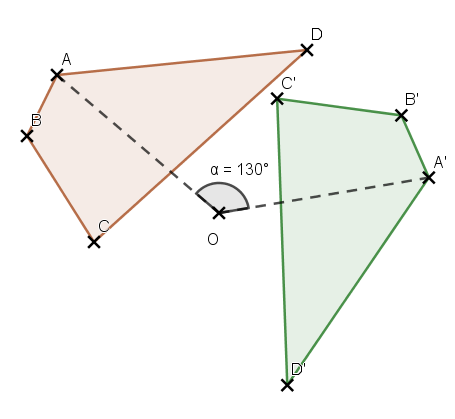
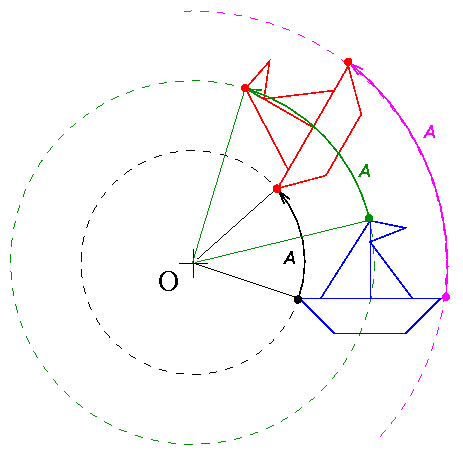
La figure verte est l’image de la figure rouge par la rotation de centre O et d’angle 130° dans le sens horaire.
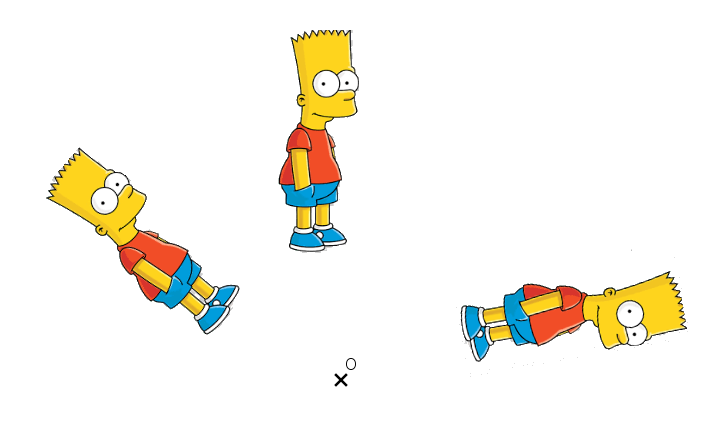
Ci-dessous, nous avons deux rotations de centre O de Bart Simpson.
La rotation de centre O et d’angle 130° dans le sens horaire puis, la rotation de centre O et d’angle 60° dans le sens anti-horaire.
La rotation conserve toutes les propriétés géométriques d’une figure.
La rotation conserve :
- les longueurs, les périmètres et les aires de figures;
- les mesures d’angles;
- l’alignement, le parallélisme et l’orthogonalité, etc…
Exemple :
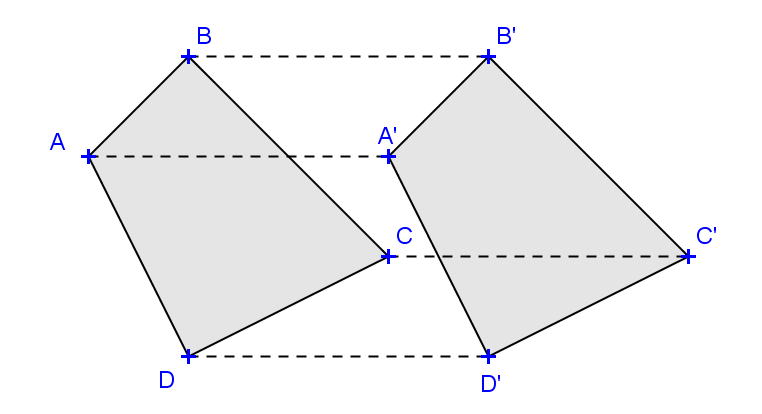
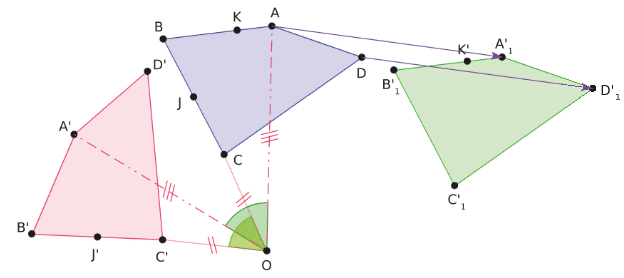
Le quadrilatère A’B’C’D’ est l’image de ABCD par la rotation de centre O et d’angle 60°.
Le quadrilatère est l’image de ABCD par la translation qui transforme A en

- Les aires et les périmètres des trois quadrilatères sont égaux.
- Les points A, B et K sont alignés, donc leurs images
sont également alignées.
- Le point J est le milieu du segment [BC] , donc son image J’ par la rotation est le milieu du segment [B’C’].
- L’angle
- L’angle
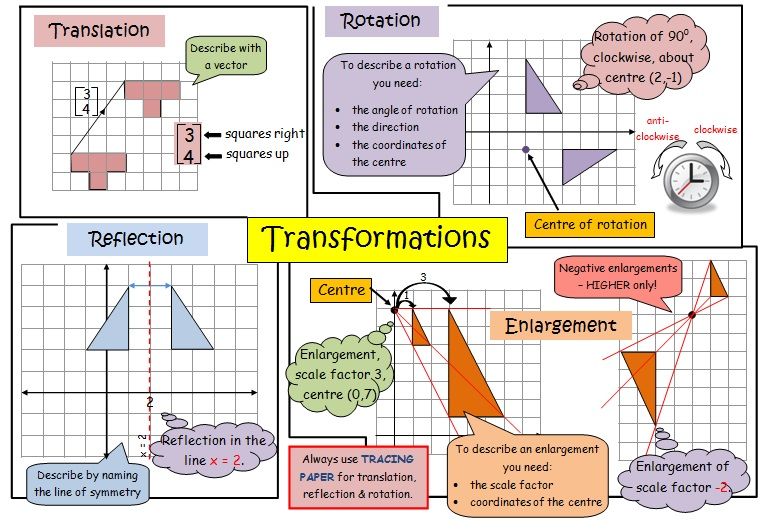
III. Carte mentale sur la translation et la rotation :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «translation et rotation : cours de maths en 4ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 4ème
Exercices de 4ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.