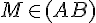Théorème de Thalès : cours de maths en 3ème à imprimer en PDF.
Mis à jour le 18 janvier 2026
O. Introduction :

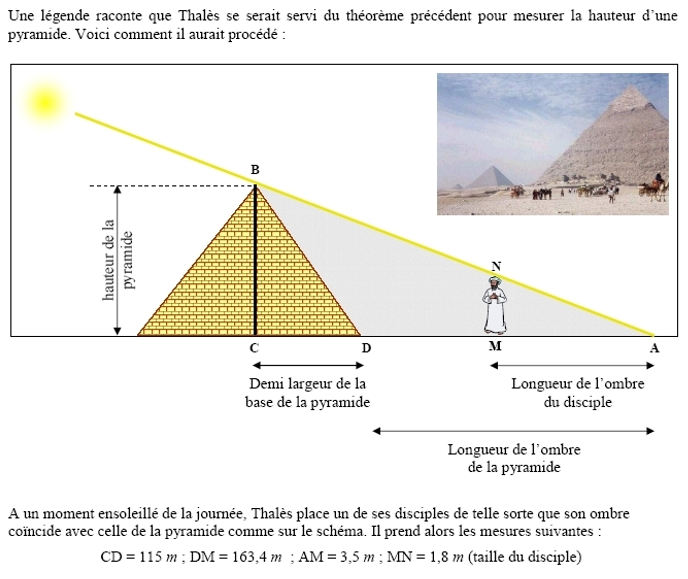
On lui attribue de nombreuses découvertes comme le calcul de la hauteur de la pyramide de Khéops située à Gizeh, le fait que les angles à la base d’un triangle isocèle sont égaux ou encore, la prédiction d’une éclipse.

I. Partie directe du théorème de Thalès :
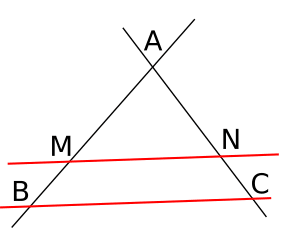
1.Les trois configurations :
2. Propriété directe du théorème de Thalès :
On considère une configuration de Thalès.
Si on a :
alors nous avons les égalités des rapports suivantes :
.
Trois configurations illustrent le théorème de Thalès dites du « triangle », du « sablier », du « huit ».
Remarque :
Les longueurs du triangle AMN sont proportionnelles aux longueurs du triangle ABC.
Remarques :
Le point A est appelé le point pivot.
Les longueurs des triangles ABC et AMN sont proportionnelles.
Exemple :
Les droites (KJ) et (PQ) sont parallèles.
Calculer la longueur du segment [IP].
On sait que 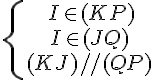
Nous avons les égalités suivantes : .
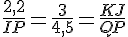
J’utilise là règle du produit en croix :
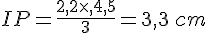
Exemple :
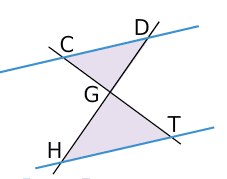
La figure ci-dessus est composée de quatre droites.
Les droites bleues sont parallèles.
DG=25 mm, GH=45 mm, CG = 20 mm, HT = 27 mm.
Les droites (DH) et (CT) sont sécantes en G.
Les droites (CD) et (HT) sont parallèles.
D’après la partie directe du théorème de Thalès, on a les égalités suivantes :
soit
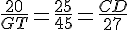
Calcul de GT :
Calcul de CD :
Remarque :
la partie directe du théorème nous permet de calculer la longueur d’un segment.
II. Partie réciproque du théorème de Thalès :
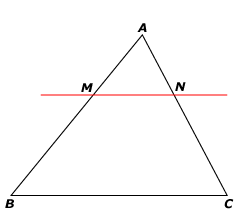
Si les points A,M,B et A,N,C sont alignés dans le même ordre
et si 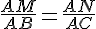
Exemple :
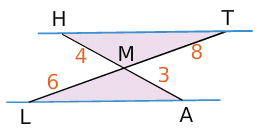
Ci-dessus, les droites (HA) et (TL) sont sécantes en M.
D’une part, , d’autre part
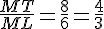
On constate que .
De plus, les points A,M,H d’une part et les points M,L,T d’autre part sont alignés dans le même ordre.
Donc, d’après la réciproque du théorème de Thalès, les droites (AL) et (HT) sont parallèles.
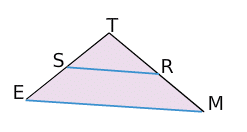
Exemple :
Ci-dessus, les droites (ES) et (MR) sont sécantes en T.
TR= 11 cm; TS = 8 cm; TM = 15 cm et TE= 10 cm.
D’une part, .
On constate que .
Or, si les droites (RS) et (ME) étaient parallèles, d’après le théorème de Thalès, il y aurait égalité.
Comme ce n’est pas le cas, les droites (RS) et (ME) ne sont pas parallèles.
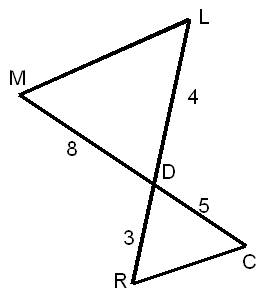
Exemple :
Les droites (ML) et (RC) sont-elles parallèles ?
Les points M,D,C et L,D,R sont alignés dans le même ordre.
Calculons séparément :
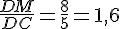
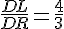
J’en déduis que 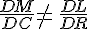
donc les droites (RC) et (ML) ne sont pas parallèles.
III. Calcul de la hauteur de la pyramide de Khéops :
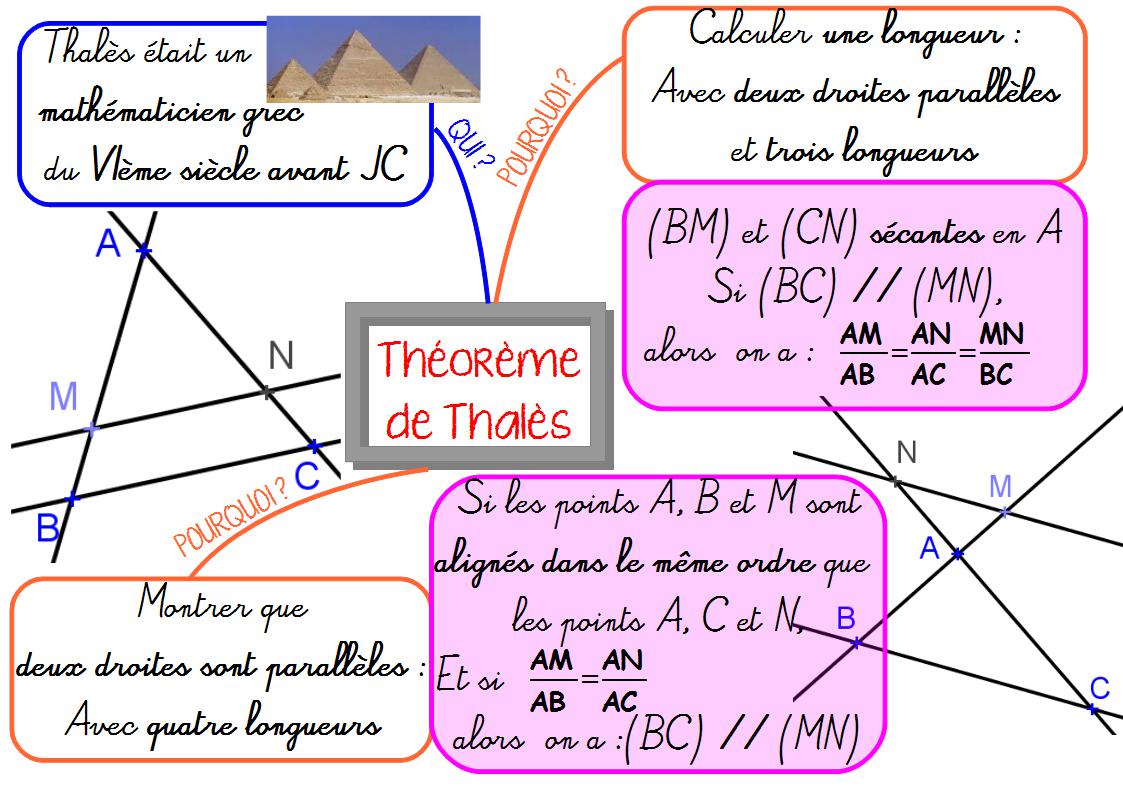
IV. Carte mentale sur le théorème de Thalès.
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «théorème de Thalès : cours de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 3ème
Exercices de 3ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.