Loi binomiale et intervalle de fluctuation : corrigé des exercices de maths en 1ère en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – pièce truquée et probabilité.
Pour le jeu de Sara :
La pièce est truquée avec une probabilité de 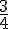
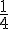
Espérance de gain pour une partie :
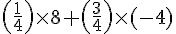
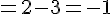
Donc, l’espérance de gain est de -1€, ce qui signifie que Sara perd en moyenne 1€ par partie. On ne doit pas lui conseiller de jouer à ce jeu.
Pour la pièce équilibrée :
La probabilité d’obtenir pile avec une pièce équilibrée est 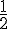
La probabilité d’obtenir uniquement face sur quatre lancers :
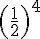
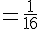
La probabilité d’obtenir au moins une pile est donc :
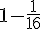
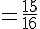
Donc, la probabilité d’obtenir au moins une pile est de 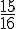
Exercice 2 – une urne contenant des boules.
Partie 1 :
Soit R le nombre de boules rouges, N le nombre de boules noires, et V le nombre de boules vertes.
Il est donné que :
- R = 2N
- V = 3R
On cherche la probabilité de tirer une boule rouge :
Nombre total de boules =
Probabilité : 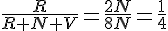
Partie 2 :
1) 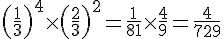
2) 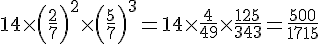
3) 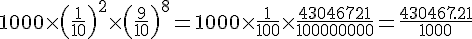
4) 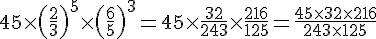
Exercice 3 – jeu de dé cubique équilibré et expérience de Bernoulli.
1) Pourquoi cette expérience aléatoire est-elle une expérience de Bernoulli ?
L’expérience est de Bernoulli car elle a deux issues possibles : soit un succès (gagner 10€ si le résultat est 5 ou 6), soit un échec (perdre 4€ autrement).
2) On note X son gain après une partie. Déterminer l’espérance de X.
La probabilité de gagner 10€ est 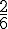
La probabilité de perdre 4€ est 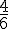
L’espérance mathématique de X est donc calculée par :
En simplifiant :
Donc, l’espérance du gain de Zehuan après une partie est 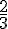
Exercice 4 – calculer des probabilités.
1. Déterminer la valeur de p .
La somme des probabilités doit être égale à 1 :
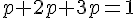
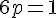
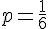
2. Calculer les probabilités.
a) 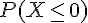
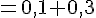
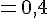
b)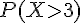
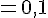
c) 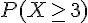
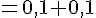
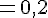
d) 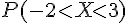
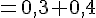
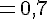
3. Calculer 
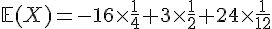
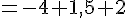
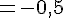
4. Déterminer la valeur de a sachant que E (X)=12.
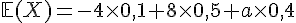
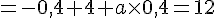
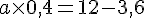
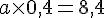
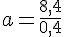
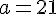
Exercice 5 – loi de probabilité d’une variable aléatoire.
Pour déterminer la valeur de a, nous utilisons la formule de l’espérance mathématique :
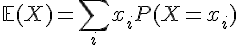
Sachant que 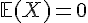
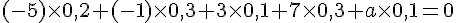
En calculant les termes, nous obtenons :
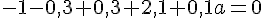
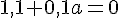
En isolant a, on obtient :
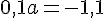
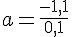
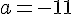
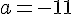
Exercice 6 – déterminer la valeur de p.
Énoncé : On nous donne la loi de probabilité d’une variable aléatoire X , et on souhaite déterminer la valeur de p .
Pour une loi de probabilité, la somme de toutes les probabilités doit être égale à 1. Ainsi, on a :
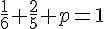
Calculons la somme des fractions connues :
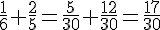
Ensuite, nous posons :
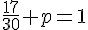
En isolant 
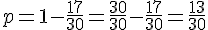
Ainsi, la valeur de p est : 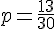
Exercice 7 – calculer des probabilités.
1. Calculons 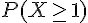
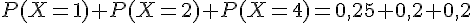
Donc, 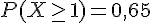
2. Calculons 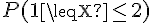
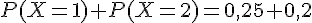
Donc, 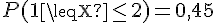
3. Calculons 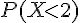
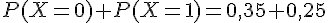
Donc, 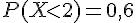
Exercice 8 – déterminer l’espérance de la variable aléatoire.
Pour déterminer l’espérance E (Y) d’une variable aléatoire, on utilise la formule :
Donc, nous avons :
Calculons chaque terme :
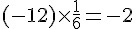
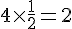
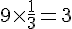
En ajoutant ces valeurs, on obtient :
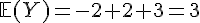
Donc, l’espérance de la variable aléatoire Y est 3.
Exercice 9 – un jeu de dominos.
Pour déterminer la loi de probabilité de la variable aléatoire S qui donne la somme des points sur un domino,
nous devons d’abord comprendre toutes les combinaisons possibles.
Un jeu de dominos double-six contient 28 dominos,
chacun représentant une somme allant de 0 (le double blanc) à 12 (le double six).
Voici une répartition des sommes possibles et des occurrences :
- Somme 0 : 1 domino (0|0)
- Somme 1 : 2 dominos (0|1), (1|0)
- Somme 2 : 3 dominos (0|2), (1|1), (2|0)
- Somme 3 : 4 dominos (0|3), (1|2), (2|1), (3|0)
- Somme 4 : 5 dominos (0|4), (1|3), (2|2), (3|1), (4|0)
- Somme 5 : 6 dominos (0|5), (1|4), (2|3), (3|2), (4|1), (5|0)
- Somme 6 : 7 dominos (0|6), (1|5), (2|4), (3|3), (4|2), (5|1), (6|0)
- Somme 7 : 6 dominos (1|6), (2|5), (3|4), (4|3), (5|2), (6|1)
- Somme 8 : 5 dominos (2|6), (3|5), (4|4), (5|3), (6|2)
- Somme 9 : 4 dominos (3|6), (4|5), (5|4), (6|3)
- Somme 10 : 3 dominos (4|6), (5|5), (6|4)
- Somme 11 : 2 dominos (5|6), (6|5)
- Somme 12 : 1 domino (6|6)
La loi de probabilité de S est donc :
| Somme | Probabilité |
|---|---|
| 0 | 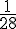
|
| 1 | 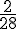
|
| 2 | 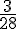
|
| 3 | 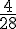
|
| 4 | 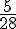
|
| 5 | 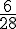
|
| 6 | 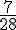
|
| 7 | 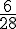
|
| 8 | 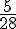
|
| 9 | 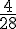
|
| 10 | 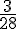
|
| 11 | 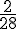
|
| 12 | 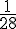
|
Exercice 10 – tirage d’un jeton dans une urne.
1. Loi de probabilité de X :
Il y a un total de 12 jetons dans l’urne : 4 jetons « 2 », 3 jetons « 4 », 3 jetons « 1 », et 2 jetons « 3 ».
La probabilité de tirer chaque numéro est donc :
– P(X=1) = 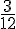
– P(X=2) = 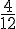
– P(X=3) = 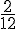
– P(X=4) = 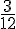
2. Loi de probabilité de Y :
– Les jetons verts comptent double : 2 devient 4, 1 devient 2.
– Les jetons rouges comptent pour moitié : 4 devient 2.
– Les jetons bleus ne changent pas : 3 reste 3.
Calculons la nouvelle loi de probabilité :
– P(Y=2) = probabilité des jetons verts « 1 » devenant « 2 » + probabilité des jetons rouges « 4 » devenant « 2 » :

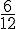
– P(Y=3) = probabilité des jetons bleus « 3 » :
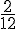
– P(Y=4) = probabilité des jetons verts « 2 » devenant « 4 » :
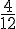
Télécharger ou imprimer cette fiche «loi binomiale et intervalle de fluctuation : corrigé des exercices de maths en 1ère en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.










