Dérivée d’une fonction : cours de maths en 1ère à imprimer en PDF.

Mis à jour le 29 mai 2025

Sommaire

La dérivée d’une fonction à travers un cours de maths en 2de avec son signe et les variations d’une fonction en 1ère ainsi que les propriétés. L’élève devra connaître les formulés de dérivation et déterminer sur quel ensemble la fonction est dérivable Étudier le taux d’accroissement et le nombre dérivé afin de déterminer le sens de variation. Il devra, également, établir le tableau de signe et de variation afin de trouver sur quels intervalles elle est croissante ou décroissante.

On considère, dans cette leçon, une fonction f définie sur un intervalle I de $\mathbb{R}$ et sa courbe représentative.

I.Nombre dérivé et tangente à une courbe

Définition : accroissement moyen.

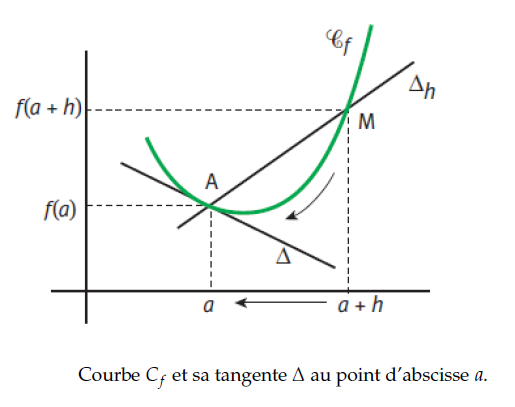
On considère deux réels distincts x_1 et x_2 appartenant à I.On appelle accroissement moyen de f entre x_1 et x_2 la quantité suivante :

$\frac{\Delta,f}{\Delta,x}(x_1;x_2)=\frac{f(x_2)-f(x_1)}{x_2-x_1}$

En notant x_1=a et x_2=a+h avec h>0, on obtient :

$\frac{\Delta,f}{\Delta,x}(a)=\frac{f(a+h)-f(a)}{h}$ .

Définition : nombre dérivé.

Si, lorsque h se rapproche de zéro, $\frac{\Delta,f}{\Delta,x}(a)$ se rapproche d’un réel , alors :On dit que la fonction f est dérivable en a.

Le réel est appelé le nombre dérivé de f en a, que l’on note f'(a) .

On écrit alors :

$\lim_{h\to,0}\frac{f(a+h)-f(a)}{h}=f'(a)$ .

Définition : tangente à une courbe.

Soient A et M deux points distincts d’une courbe.Géométriquement, la tangente à la courbe au point A est la position limite de la sécante (AM)

lorsque M se rapproche de A

Propriété : coefficient directeur de la tangente.

Le nombre dérivé

est le coefficient directeur de la tangente à la courbe

au point d’abscisse

Propriété : équation réduite de la tangente.

Soit f une fonction dérivable en de courbe représentative C_f .L’équation réduite de la tangente à C_f en est donnée par la formule suivante :

II.La dérivée d’une fonction

Définition :

Si, pour tout réel $a\in,I,,f'(a)$ existe, on dit que f est dérivable en I.On définit alors, une nouvelle fonction f’ sur I par $f':x,\mapsto ,f'(x)$ .

Propriété : dérivées des fonctions usuelles.

Propriété : dérivée d’une somme ou produit.

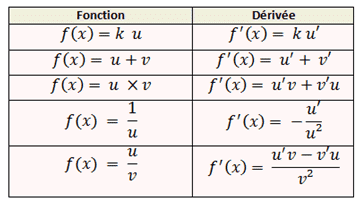
Soient et deux fonctions définies et dérivables sur I un intervalle de R et k un nombre réel.

La fonction $u+v:x,\mapsto ,u(x)+v(x)$ est dérivable sur I et on a .
La fonction $ku:x,\mapsto ,k\times ,u(x)$ est dérivable sur I et on a $(ku)'=k\times ,u'$ .
La fonction $uv:x,\mapsto ,u(x)\times ,v(x)$ est dérivable sur I et on a .

Propriété : dérivée de l’inverse et d’un quotient.

Soient et deux fonctions définies et dérivables sur I un intervalle de R telle que ne s’annule pas sur I.

La fonction $\frac{1}{u}:x,\mapsto ,\frac{1}{u(x)}$ est dérivable sur I et on a $(,\frac{1}{u})'=-\frac{u'}{u^2}$ .
La fonction $\frac{u}{v}:x,\mapsto ,\frac{u(x)}{v(x)}$ est dérivable sur I et on a $(,\frac{u}{v})'=,\frac{u'v-uv'}{v^2}$ .

Autre version de cette leçon

I. Nombre dérivé et dérivée d’une fonction

f est une fonction définie sur un intervalle I.

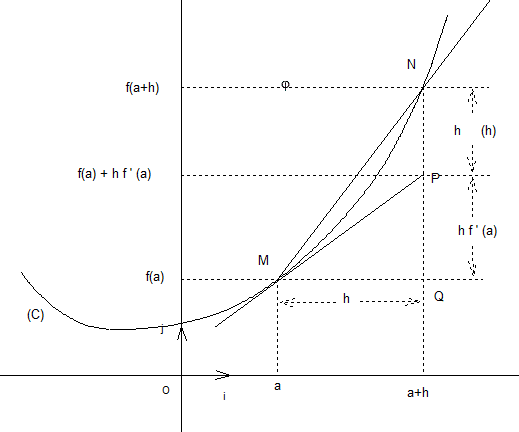
La courbe (C) ci-dessous est la représentation graphique de f dans un repère orthonormal $(O,\vec{i},\vec{j})$ .

M et N sont deux points de (C) d’abscisses respectives $a\in\,I$ et $x\,=\,a\,+\,h\,\in\,I$ où $h\in\,\mathbb{R}^*$ .

Définition 1

Si f est une fonction définie sur un intervalle I et si $a\in\,I$ .
Lorsqu’il existe un nombre réel d tel que, pour tout réel h proche de 0, on ait:

$\lim_{h\,\to\,0}\frac{f(a+h)-f(a)}{h}=d$

On dit que la fonction f est dérivable en a et que d = f ‘(a) est le nombre dérivé de f en a.

Définition 2

Si f est une fonction définie sur un intervalle I et si a $\in$ I.
Lorsqu’il existe un nombre réel d tel que, pour tout réel x $\in$ I et proche de a, on ait:

$\lim_{x,\to,a}\frac{f(x)-f(a)}{x-a}=d$

On dit que la fonction f est dérivable en a et que d = f ‘(a) est le nombre dérivé de f en a.

II. Fonction dérivable sur un intervalle I

Définition :

On dit que f est dérivable sur un intervalle I lorsqu’elle est dérivable en tout point de I

Remarques sur les notations et les « manies des physiciens »

Les physiciens expriment la différence h = x – a par la le symbole $\Delta\,x$ (accroissement de la variable x au voisinage du point a) et la différence f(x) – f(a) par $\Delta\,y$ ( accroissement correspondant entre les images de x et de a qu’ils assimilent aux ordonnées y).

Avec ces notations, ils écrivent alors au voisinage de a: $\lim_{\Delta\,x\,\to\,0}\frac{\,\Delta\,y}{\Delta\,x\,}=f'(a)$ .

De façon générale, sur un intervalle I, en notant « y » la fonction « f », la fonction dérivée de y sera notée: $f'=\frac{dy}{dx}$ .

Historiquement, la notation $f\,'(x)$ est due à Newton et la notation différentielle $\frac{dy}{dx}$ provient de Leibniz.

III. Equation de la tangente et approximation affine de f au voisinage de x = a

En reprenant les données du début de la leçon et l’illustration graphique et en supposant que la fonction f est dérivable en a:
La tangente (MP) à la courbe (C) en M d’abscisse a existe.Elle a pour coefficient directeur m = f ‘(a).Son équation est donc de la forme: y = mx + p, où m = f ‘(a) et son ordonnée à l’origine p est à calculer.
Pour cela, il suffit d’écrire que (MP) passe par M( a ; f(a) ).On a donc: $f(a)\,=,f\,'(a)\,\times \,a\,+\,p$ .
Ceci donne: $p\,=\,f(a)\,-\,a\,f\,'(a)$ .Donc y = f ‘(a) x + f(a) – a f ‘(a) que l’on écrit souvent sous l’une des formes, plus faciles à retenir:

$\mathbf{y\,=\,f\,'(a)\,(x-a)\,+\,f(a)}$ ou $\mathbf{y\,-\,f(a)\,=\,f\,'(a)\,(x-a)}$ .

Donc, la tangente (MP) à la courbe (C) en M est la représentation graphique de la fonction affine g:

$g:x\,\mapsto \,f'(a)(x-a)+f(a)$

Montrons que cette fonction affine est une approximation de la fonction f lorsque x est proche de a.
En effet, l’ordonnée du point P d’abscisse x = a + h est: $g(x)\,=\,f\,'(a)\,(x-a)\,+\,f(a)$ .

Elle s’écrit aussi: $g(a\,+\,h)\,=\,f\,'(a)\,(a\,+\,h\,-\,a)\,+\,f(a)$ , c’est à dire: $g(a\,+\,h)\,=\,f(a)\,+\,h\,f\,'(a)$ .

Or, f(a+h) = f(a) + h f ‘(a) + h $\varphi$ (h) avec $\lim_{h\,\to\,0}\varphi\,(h)=\,0$ .

On en déduit que, lorsque h est voisin de zéro, on a: f(a+h) $\approx$ f(a) + h f ‘(a).

On peut donc conclure que, lorsque x est voisin de a, la fonction affine $g:x\,\mapsto \,f'(a)(x-a)+f(a)$ est une approximation de la fonction .

On peut même montrer, mais nous l’admettrons ici, que c’est la meilleure approximation affine de f au voisinage de a.

IV.La dérivée des fonctions usuelles.

V.Les formules de dérivation

VI. Signe de la dérivée et sens de variation d’une fonction

1.Rappels sur la dérivée des fonctions usuelles

2.Rappels sur les formules de dérivation

Nous admettrons sans démonstration les théorèmes suivants:

Théorème 1:

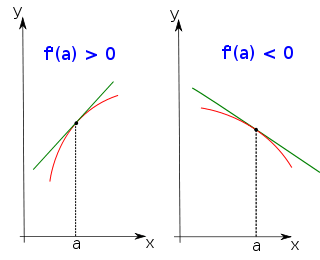
Si f est une fonction dérivable sur un intervalle [ a ; b ],
· Si, pour tout x $\in$ ] a ; b [, on a: f ‘(x) $\geq\,$ 0, alors f est croissante sur [ a ; b ].
· Si, pour tout x $\in$ ] a ; b [, on a: f ‘(x) $\leq\,$ 0, alors f est décroissante sur [ a ; b ].
· Si, pour tout x $\in$ ] a ; b [, on a: f ‘(x) = 0, alors f est constante sur [ a ; b ].

Théorème 2:

Si f est une fonction dérivable sur un intervalle I,
· Si, pour tout x $\in$ I, on a: f ‘(x) > 0 ( sauf peut-être en des points isolés où f ‘(x) = 0 ),
alors f est strictement croissante sur I.
· Si, pour tout x $\in$ I, on a: f ‘(x) < 0 ( sauf peut-être en des points isolés où f ‘(x) = 0 ),
alors f est strictement décroissante sur I.

Notons deux cas particuliers utiles:

Propriété :

Si f est une fonction dérivable sur un intervalle [ a ; b ],
· Si, pour tout x $\in$ ] a ; b [, on a f ‘(x) > 0 , alors f est strictement croissante sur [ a ; b ].
· Si, pour tout x $\in$ ] a ; b [, on a f ‘(x) < 0 , alors f est strictement décroissante sur [ a ; b ].

Exemples:

1) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = x². f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 2x.
· Pour tout x $\in$ ]- $\infty$ ; 0 ], on a f ‘(x) £ 0, donc f est décroissante sur ]- $\infty$ ; 0 ].
· Pour tout x $\in$ [ 0 ; + $\infty$ [, on a f ‘(x) ³ 0, donc f est croissante sur [ 0 ; + $\infty$ [.
· Pour tout x $\in$ ]- $\infty$ ; 0 [, on a f ‘(x) < 0, donc f est strictement décroissante sur ]-¥ ; 0 ].
· Pour tout x $\in$ ]0 ; + $\infty$ [, on a f ‘(x) > 0, donc f est strictement croissante sur [ 0 ; + $\infty$ [.

2) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = x³. f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 3x².
· Pour tout x $\in$ $\mathbb{R}$ , on a f ‘(x) ³ 0, donc f est croissante sur $\mathbb{R}$ .
· Pour tout x $\in$ ]- $\infty$ ; 0 [ È ]0 ; + $\infty$ [, on a f ‘(x) > 0, donc f est strictement croissante sur $\mathbb{R}$ .

3) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = 2. f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 0.
· Pour tout x $\in$ $\mathbb{R}$ , on a f ‘(x) = 0, donc f est constante sur $\mathbb{R}$ .

Nous admettrons sans démonstration les théorèmes suivants:

Théorème 3:

Si f est une fonction dérivable sur un intervalle I.
Si f admet un maximum local (ou un minimum local) en x = a différent des extrémités de l’intervalle I, alors: f ‘(a) = 0.

Théorème 4:

Si f est une fonction dérivable sur un intervalle I.
Si a $\in$ I et a différent des extrémités de I.
Si f ‘(x) s’annule pour x = a en changeant de signe.
Alors f(a) est un extremum local de f sur I.

Exemples:
1) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = x². f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 2x.
f ‘(x) s’annule en x = 0 en changeant de signe, donc f(0) = 0 est un extremum local de f.
Cet extremum est en réalité un minimum, car f est strictement décroissante sur ]- $\infty$ ; 0 ] et strictement croissante sur [ 0 ; + $\infty$ [. Ceci peut se résumer dans un tableau de variation.
2) Soit la fonction f définie sur $\mathbb{R}$ par f(x) = x³. f est dérivable sur $\mathbb{R}$ avec f ‘(x) = 3x².
f ‘(x) s’annule en x = 0 sans changer de signe, il n’y a donc pas d’extremum en x = 0.

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «dérivée d'une fonction : cours de maths en 1ère à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.