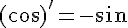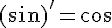Fonctions cosinus et sinus : cours de maths en terminale à imprimer en PDF.

Accueil >> Cours de maths >> Cours en Terminale >> Fonctions cosinus et sinus : cours de maths en terminale à imprimer en PDF.

Mis à jour le 20 décembre 2025

📚Cours de MathématiquesTerminale • lycée
Fonctions cosinus et sinus
⏱️Temps de lecture : 3 min
🎯Difficulté : Expert
📚Cycle terminal
📋Prérequis : Programme 1ère maîtrisé
📄Format PDF disponible gratuitement
Les fonctions cosinus (cos) et sinus (sin) à travers un cours de maths en terminale complet. L’élève devra être capable de déterminer l’ensemble de définition de ces fonctions mais également, justifier si elle est périodique. Connaître et savoir appliquer les différentes formulés et étudier la parité paire ou impaire) en terminale.

I. Définitions et rappels

On considère un repère orthonormé direct du plan.

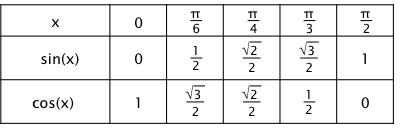
Le point M image d’un réel x sur le cercle trigonométrique de centre O , a pour coordonnées (cos x; sin x) où cos x est le cosinus de x et sin x est le sinus de x.

tableau valeurs cos sin

Définition :

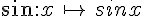
La fonction cosinus, notée cos, est la fonction définie sur \mathbb{R} par cos:x\,\mapsto\,cosx ;La fonction sinus, notée sin, est la fonction définie sur \mathbb{R} par sin:x\,\mapsto\,sinx .

II. Propriétés des fonctions sinus et cosinus

Définition : fonction périodique.

Soit f une fonction définie sur R et un nombre réel T.

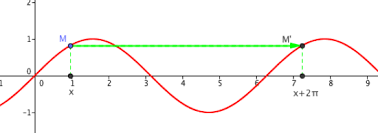
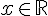
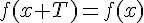
La fonction f est périodique de période T ou T-périodique si pour tout x\in\mathbb{R} , f(x+T)=f(x) .

fonction périodique

Définition : fonction paire ou impaire.

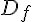
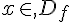
Soit f une fonction définie sur un ensemble D_f symétrique par rapport à zéro.Une fonction f est paire si pour tout x\in,D_f , f(-x)=f(x) .

fonction paire

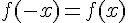
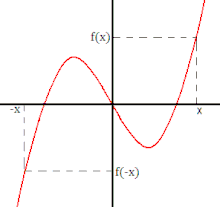
Une fonction f est impaire si pour tout 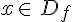x\in\,D_f , f(-x)=-f(x) .

fonction impaire

Propriété :

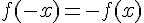
Les fonctions cos et sin sont 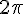2\pi -périodiques.

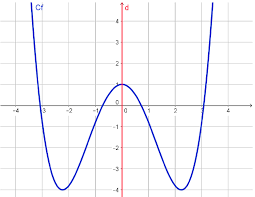
La fonction cos est paire et la fonction sin est impaire.

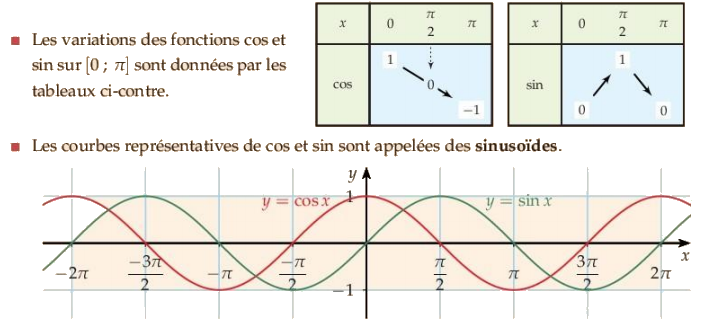
III. Dérivabilités et variations de ces fonctions

Propriété : dérivées des fonctions cos et sin.

Les fonctions cos et sin sont dérivables et continues sur R.

  • (cos)'=-sin
  • (sin)'=cos
Propriété :
variations cos sin
Propriété :
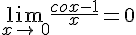
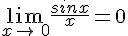
\lim_{x\rightarrow\,0}\frac{cox-1}{x}=0    et \lim_{x\rightarrow\,0}\frac{sinx}{x}=0 .

 

 

 

4.8/5 - (34087 votes)
Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «fonctions cosinus et sinus : cours de maths en terminale à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de Terminale

cours terminale
Suites numériques
cours terminale
Nombres complexes
cours terminale
Produit scalaire dans l’espace
cours terminale
Fonction logarithme népérien

Exercices de Terminale

vecteurs espace exercices maths terminale
Vecteurs de l’espace
fonction exponentielle exercices maths terminale
Fonction exponentielle
limites suites espace exercices maths terminale
Limites de suites
equations parametriques droites plans exercices maths terminale
Les équations paramétriques et cartésiennes de droites

Exercices de maths corrigés sous forme d'escape game avec MATHS PDF.

📚✏️
👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices
Nos applications

Téléchargez la dernière version gratuite de nos applications.

Nombre de fichiers PDF téléchargés.  Maths PDF c'est 14 801 947 cours et exercices de maths téléchargés en PDF et 4 250 exercices.