Le raisonnement par récurrence : cours de maths en terminale.

Sommaire

Le raisonnement par récurrence, ou encore, appelé principe de récurrence dans un cours de maths en terminale. C’est une technique utilisée en pour prouver qu’une affirmation est vraie pour tous les nombres entiers positifs n. L’élève devra être capable de démontrer une propriété en utilisant les étapes d’initialisation, d’hérédité puis la conclusion.

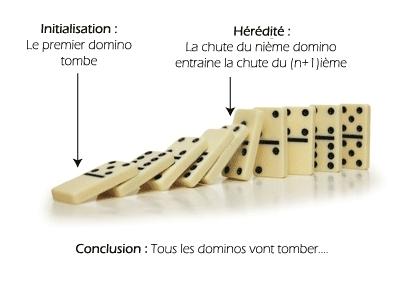
Ce pri,cime peur être comparé à des dominant qui tomberai en provoquant la chute du suivant.

La technique consiste à prouver le cas de base, qui est généralement n=1, puis à prouver que si l’affirmation est vraie pour un certain nombre entier k, elle doit également être vraie pour le nombre entier suivant k+1.

I.Axiome de récurrence

Axiome :

Soit P(n) une propriété dépendant d’un entier naturel n. Si on démontre les deux conditions suivantes :

Initialisation : P(n) est vraie pour un entier .
Hérédité : pour tout entier naturel $k\geq\,\,n_0$ , P(n) est vraie alors on peut affirmer que P(n) est vraie pour tout entier $n\geq\,\,n_0$ .

Remarque :

La propriété P(n) peut être de différentes natures :Une égalité :

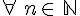
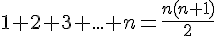
$\forall\,n\in\,\mathbb{N}$ , P(n) : $1+2+3+...+n=\frac{n(n+1)}{2}$ .

Une inégalité :

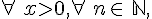
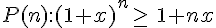
$\forall\,x>0,\forall\,n\in\,\mathbb{N},$ $P(n):(1+x)^n\geq\,\,1+nx$ .

Une phrase :

Pour tout entier naturel n, P(n) : 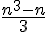$\frac{n^3-n}{3}$ est un entier naturel.

Remarque :

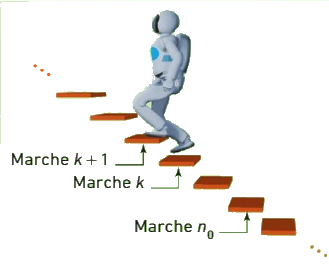
On peut illustrer le raisonnement par récurrence par la programmation d’un robot qui doit monter des escaliers.

Si le robot est mis sur une marche 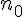n_0 de l’escalier et si le robot sait monter

d’une marche à la marche suivante alors le robot saura monter toutes les marches de l’escalier

à partir de la marche 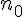n_0 .

II. Le raisonnement par récurrence et la démonstration

Utiliser le raisonnement par récurrence :

L’initialisation est la démonstration que 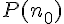P(n_0) est vraie. L’hérédité est une implication à montrer.

On considère un entier 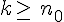$k\geq\,\,n_0$ et on suppose que P(k) est vraie.

C’est-à-dire que la propriété est vraie au rang k.

Cela s’appelle l’hypothèse de récurrence.

On démontre que P(k+1) est alors vraie en utilisant l’hypothèse de récurrence.

On aboutit à la conclusion que P(n) est vraie pour tout entier $n\geq\,\,n_0$ .

Exemple :

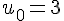
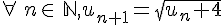
On considère la suite numérique définie par et $\forall\,n\in\,\mathbb{N},u_{n+1}=\sqrt{u_n+4}$ .

Démontrer par récurrence que 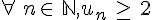$\forall\,n\in\,\mathbb{N},u_n\,\geq\,\,2$ .

Initialisation :

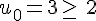
$u_0=3\geq\,\,2$ donc P(0) vraie.

Hérédité :

Supposons qu’il existe un entier k tel que 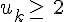$u_k\geq\,\,2$

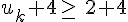
$u_k+4\geq\,\,2+4$

Or la fonction racine carrée est croissante sur 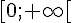$[0;+\infty[$ .

donc $\sqrt{u_k+4}\geq\,\,\sqrt{6}\geq\,\,\sqrt{4}$

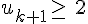
donc $u_{k+1}\geq\,\,2$ ainsi, P(k+1) est vraie.

La propriété est héréditaire.

Conclusion :

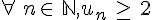
$\forall\,n\in\,\mathbb{N},u_n\,\geq\,\,2$

III. Principe de récurrence et dominos

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «le raisonnement par récurrence : cours de maths en terminale à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

D'autres cours et exercices à consulter

Maths PDF c'est 13 317 812 cours et exercices de maths téléchargés en PDF et 4 250 exercices.