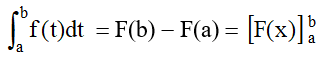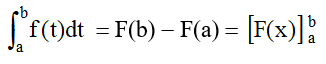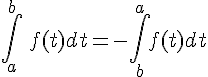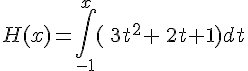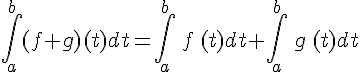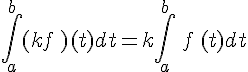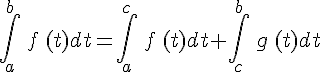Intégrale : cours de maths en terminale à imprimer en PDF.
Mis à jour le 10 février 2026
Les intégrales à travers un cours de maths en terminale complet à télécharger en PDF. Vous devrez avoir assimilé le chapitre sur la dérivée afin de pouvoir déterminer une primitive d’une fonction. L’élève devra avoir compris la signification concrète d’une intégrale avec l’aire d’une surface en terminale.
I. Définitions et propriété de l’intégrale et des primitives.
En particulier, les fonctions dérivables sur un intervalle I, sont intégrables sur I, mais cette condition, bien que suffisante n’est pas nécessaire. La fonction f définie sur

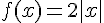


Cependant, sauf cas particulier contenant des indications, dans les problèmes de bac, les fonctions intégrables sur un intervalle I seront toujours des fonction dérivables sur I.
alors quels que soient a


F(b) – F(a) = G(b) – G(a)En effet, si F ‘(x) = G ‘(x), alors, il existe c


Donc: G(b) – G(a) = F(b) + c – [F(a) + c] = F(b) – F(a).
Remarque:
La différence des images de b et de a, pour n’importe quelle primitive de f est la même.
Ce nombre ne dépend donc que de f, de a et b.
Ceci va nous permettre de donner la définition suivante:
Soient a


L’intégrale de a à b de la fonction f est le nombre F(b) – F(a) où F est une primitive quelconque de f sur I.
Notation:
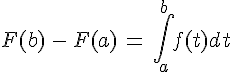
Dans l’écriture 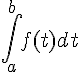
En effet, on peut aussi écrire 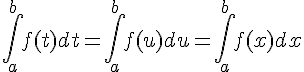
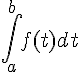
Exemple :
La fonction 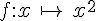

Elle est donc intégrable sur 

Par exemple 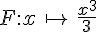

II.Conséquences de la définition: premières propriétés.
Soit f une fonction dérivable sur un intervalle [a,b].


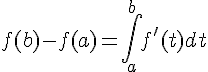
On déduit de cette propriété une importante synthèse qui relie une fonction dérivable, sa fonction dérivée et la notion d’intégrale.

Alors, pour tout x

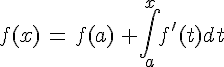 .
.III.Fonction primitive d’une fonction intégrable.

la fonction
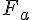
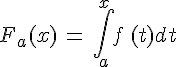 est la primitive de f qui s’annule en x = a.
est la primitive de f qui s’annule en x = a.Démonstration :
Si G est une primitive quelconque de f sur I, alors 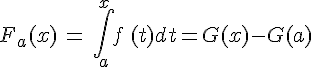
Fa‘(x) = G ‘(x) = f(x) .
En effet, G(a) est une constante, sa dérivée est donc nulle et G ‘(x) = f(x) car G est une primitive de f. Conclusion: 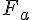
De plus: Fa (a) = G(a) – G(a )= 0, donc Fa s’annule pour x=a .
Exercice :
Calculer les intégrales suivantes, puis indiquer les primitives qu’elles définissent.
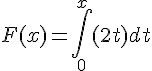
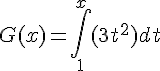
IV. Intégrale d’une fonction positive.

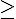
Appelons F une primitive de f sur [a;b].On a alors F ‘(x) = f(x) pour tout x

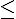
Donc:
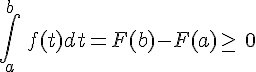 .
.
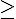
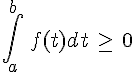 .
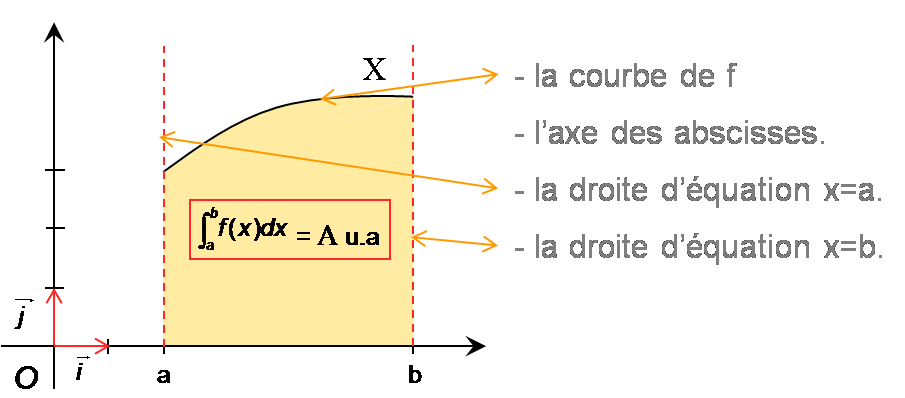
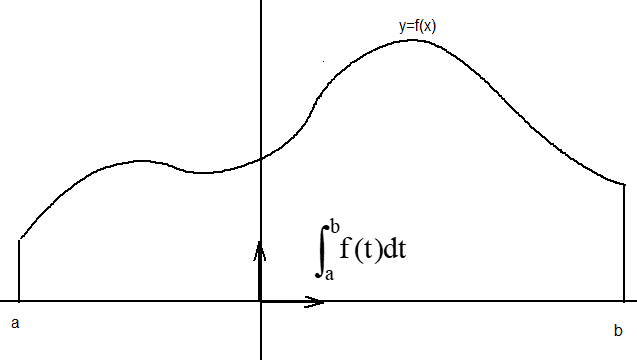
.V. Les intégrales et les aires
1.Tableau récapitulatif
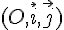
a
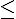
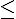
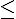
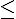
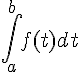 unités d’aireL’unité d’aire étant celle du rectangle dont les côtés sont les unités de longueur des abscisses et des ordonnées.
unités d’aireL’unité d’aire étant celle du rectangle dont les côtés sont les unités de longueur des abscisses et des ordonnées.L’ensemble D est constitué des points situés entre la courbe représentative de la fonction f, l’axe des abscisses et les droites d’équation x = a et x = b.
On considère f une fonction continue et positive sur un intervalle [a,b].La fonction 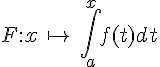
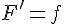
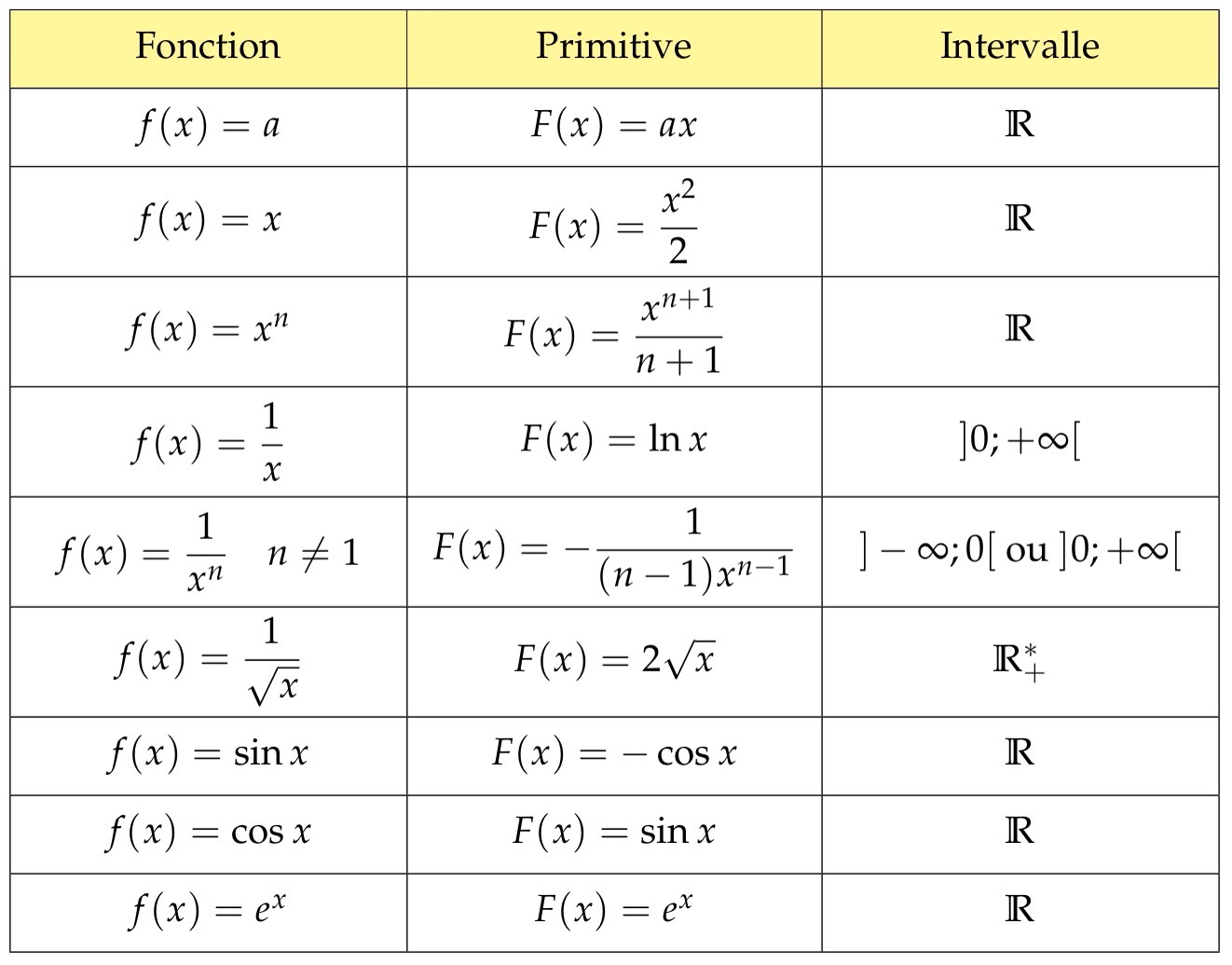
VI. Primitive d’une fonction continue
On considère f une fonction continue sur un intervalle I.Une primitive de f est une fonction F définie et dérivable sur I telle que 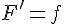
On considère f une fonction continue sur un intervalle I et F une primitive de f sur I.La fonction f admet une une infinité de primitives sur I qui sont de la forme .
Soient 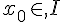
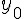
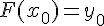
On considère une fonction f continue sur un intervalle [a;b] et F une primitive de f sur [a;b].Nous avons 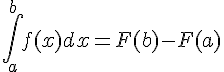
Exemple :
Calculer la valeur de l’intégrale suivante :
![\int_{0}^{3}x^2dx=[\frac{x^3}{3}]=(\frac{3^3}{3}-\frac{0^3}{3})=9](https://maths-pdf.fr/latex-images/3b5a5df0fbb3c8735ea8ae5c9abc96f9.png)
On considère f et g deux fonctions continues sur un intervalle [a,b] et k un nombre réel.
On considère f une fonction continue et négative sur un intervalle [a,b].L’aire du domaine situé entre 
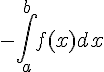
On considère f une fonction continue et négative sur un intervalle I et a,b,c trois nombres réels appartenant à I.
Soient f et g deux fonctions continues sur un intervalle [a,b].Si f est positive sur [a,b] alors 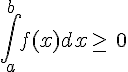
Si pour tout ![x\in[a,b]](https://maths-pdf.fr/latex-images/c7c42309c359c25dfe77f397d5261997.png)
alors
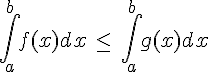
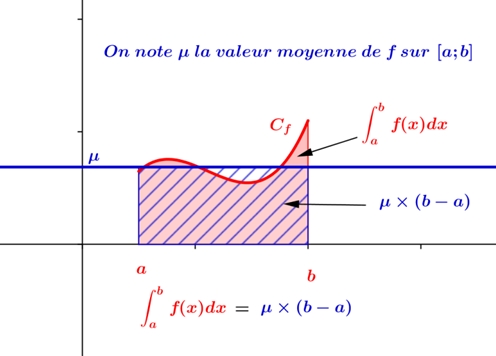
On considère f une fonction continue sur un intervalle [a,b].
La valeur moyenne de f sur [a,b] est le nombre 
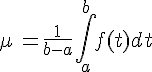
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «intégrale : cours de maths en terminale à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Terminale
Exercices de Terminale
Nos applications
Téléchargez la dernière version gratuite de nos applications.