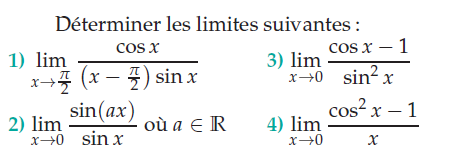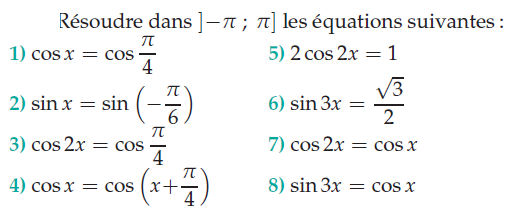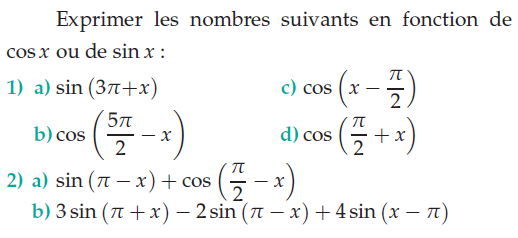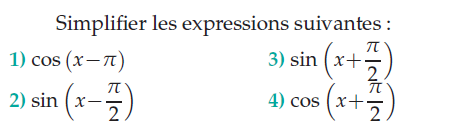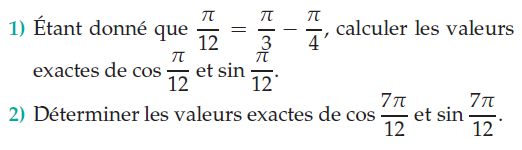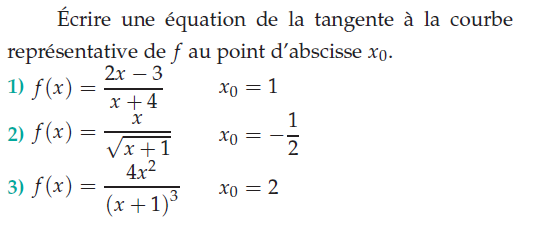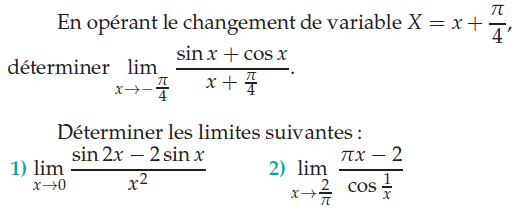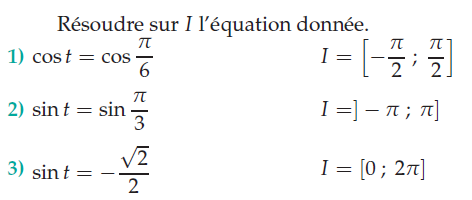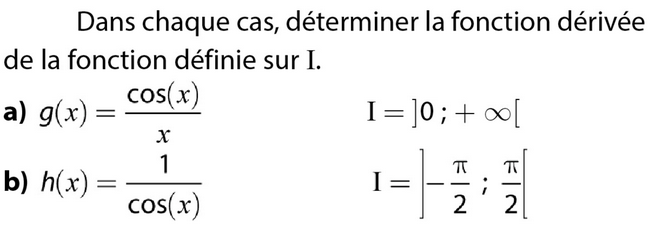Fonctions sinus et cosinus : exercices de maths en terminale corrigés en PDF.
Mis à jour le 24 novembre 2025
Des exercices de maths en terminale portant sur les fonctions sinus et cosinus afin de réviser en ligne et de développer ses compétences.
Exercice 1 – f dérivable et tableau de variation.
Exercice 2 – déterminer les limites suivantes.
Exercice 3 – résoudre les équations.
Exercice 4 – une étude de la dérivabilité de la fonction cosinus.
Exercice 5 – fonction homographique et polynôme.
Exercice 6 – exprimer les nombres en fonction de cosx et sinx.
Exercice 7 – simplifier les cos et sin suivants.
Exercice 8 – déterminer la valeur de cosinus et sinus.
Exercice 9 – simplifier et résoudre des équations.
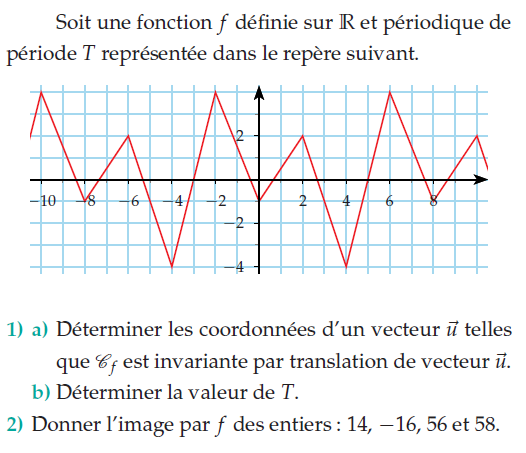
Exercice 10 – déterminer les coordonnées d’un vecteur.
Exercice 11 – vérifier que la fonction est T-Périodique.
Exercice 12 – fonction paire ou impaire.
Exercice 13 – périmètre du rectangle et calcul formel.
Exercice 14 – dresser le tableau de variation.
Exercice 15 – déterminer la fonction dérivée.
Exercice 16 – conjecturer avec la calculatrice une limite.
Exercice 17 – convergence de suites et cosinus.
Exercice 18 – cosinus et sinus avec tableau de variation.
Exercice 19 – démontrer la dérivée nième d’une fonction.
Exercice 20 – valeurs où la dérivée s’annule.
Exercice 21 – montrer que f est dérivable.
Exercice 22 – une équation de la tangente à la courbe.
Exercice 23 – montrer que f admet un minimum.
Exercice 24 – justifier que f est dérivable sur I.
Exercice 25 – calculer la dérivée de fonctions contenant cos x et sin x.
Exercice 26 – changement de variable et calcul de limite.
Exercice 27 – courbes d’équations du type y=asin(wx).
Exercice 28 – pour les affirmations suivantes, démêler le vrai du faux.
Exercice 29 – déterminer l’ensemble de dérivabilité.
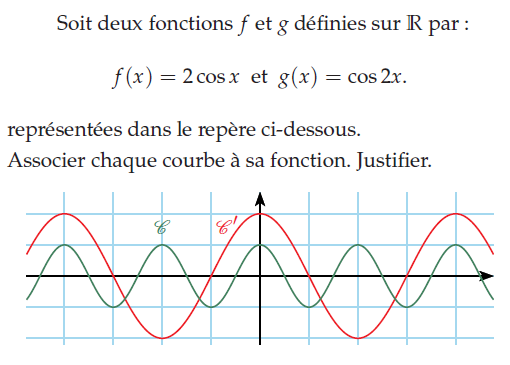
Exercice 30 – fonction cosinus et représentations graphiques.
Exercice 31 – résoudre sur I l’équation donnée.
Exercice 32 – fonction définie et dérivable en x0.
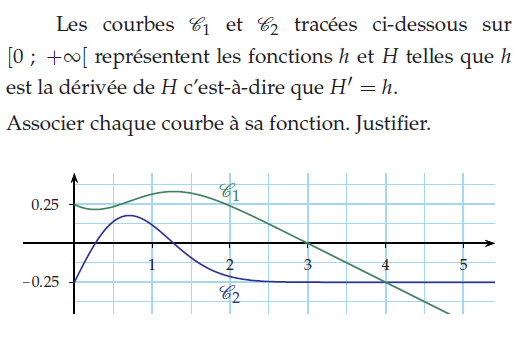
Exercice 33 – associer chaque courbe à sa fonction.
Exercice 34 – vérifier que la fonction f est T-périodique.
Exercice 35 – déterminer l’ensemble de dérivabilité.
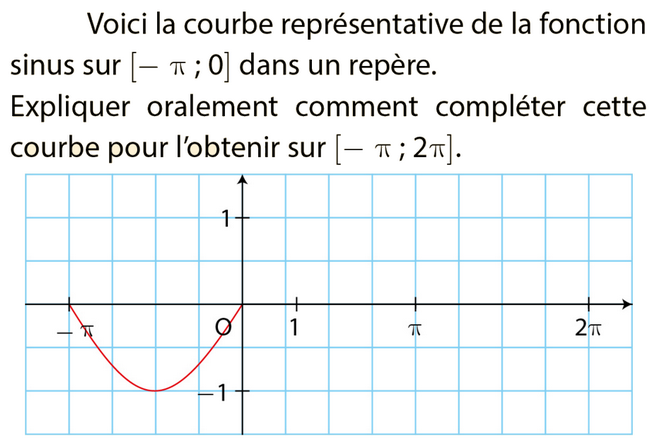
Exercice 36 – courbe représentative de la fonction sinus.
Exercice 37 – fonction sinus et affirmations.
Exercice 38 – quel est le sens de variation ?.
Exercice 39 – démontrer que la fonction f est périodique.
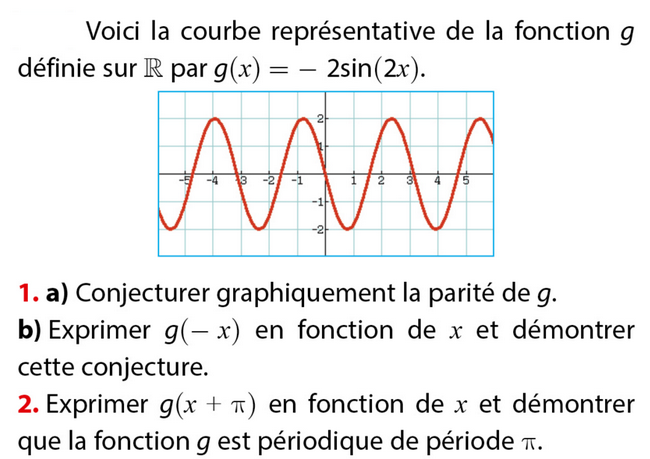
Exercice 40 – étude de la parité et de la périodicité.
Exercice 41 – démontrer que la fonction h est impaire.
Exercice 42 – conjecturer que la fonction k est périodique.
Exercice 43 – déterminer la fonction dérivée.
Exercice 44 – etude d’une fonction et tableau de variation.
Exercice 45 – dérivée et tableau de variation.
Exercice 46 – exprimer f(x+2) et conclure.
Exercice 47 – propriétés d’une fonction et calcul formel.
Exercice 48 – déterminer dans chaque cas la fonction dérivée.
Exercice 49 – déterminer la fonction dérivée définie sur I.
Exercice 50 – étudier f ‘(x) et dresser le tableau de variation.
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «fonctions sinus et cosinus : exercices de maths en terminale corrigés en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Terminale
Exercices de Terminale
Nos applications
Téléchargez la dernière version gratuite de nos applications.

.png)