Géométrie dans l’espace : cours de maths en 2de à imprimer en PDF.
Mis à jour le 16 mars 2025

I. Repérage sur la sphère terrestre
1. La sphère terrestre
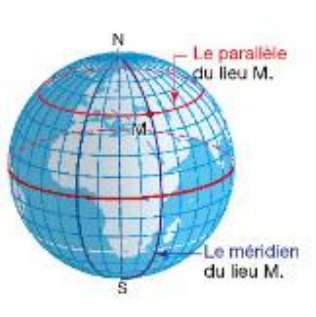
La sphère de centre O et de rayon R est formée des points M de l’espace tels que OM=R.On assimile la terre à une sphère de rayon 6 400 km et de centre O. Les points N et S représentent respectivement le pôle nord et le pôle sud.
M est un point de la sphère terrestre distinct des pôles N et S.Le méridien du lieu M est le demi-cercle de diamètre [NS] passant par M.
Le parallèle du lieu M est le cercle section de la sphère par le plan passant par M et perpendiculaire à la droite (NS).
L’équateur est le seul parallèle qui est un grand cercle (de centre O) de la sphère.
2. Repérage sur la sphère terrestre
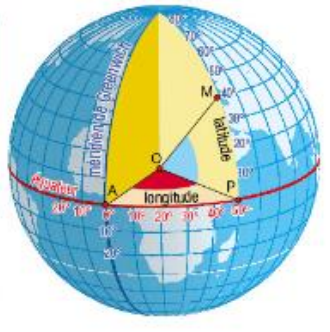
M est un plan de la sphère distinct des pôles N et S.Le méridien de M coupe l’équateur en P et le méridien de Greenwich coupe l’équateur en A.
- La longitude du lieu M est la mesure, en degrés, de l’angle
suivie de l’indication ouest(O) ou est (E).
- La latitude du lieu M est la mesure, en degrés, de l’angle
suivie de l’indication nord (N) ou sud (S).
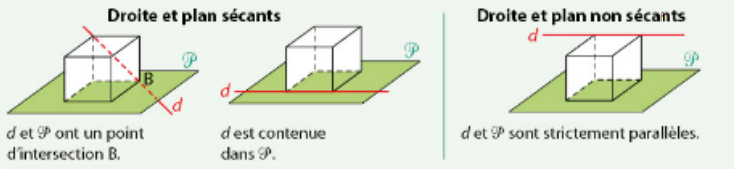
II. Positions relatives de droites et plans
1. Règle d’incidence.
- Par deux points distincts de l’espace, il passe une unique droite;
- Par trois points non alignés A,B et C de l’espace, il passe un unique plan noté (ABC);
- Si deux points distincts A et B de l’espace appartiennent à un plan P, alors tout point de la droite (AB) appartient au plan P. On dit que la droite (AB) est contenue dans le plan P et on note
.
- Dans chaque plan de l’espace, on peut appliquer tous les théorèmes de géométrie plane.
2.Les positions relatives.
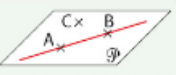
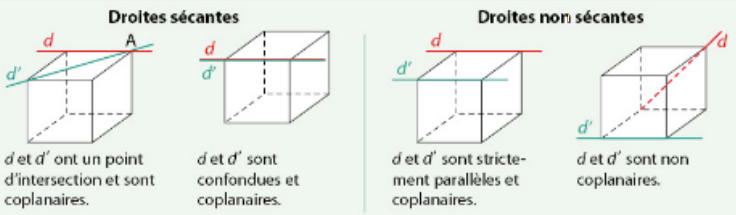
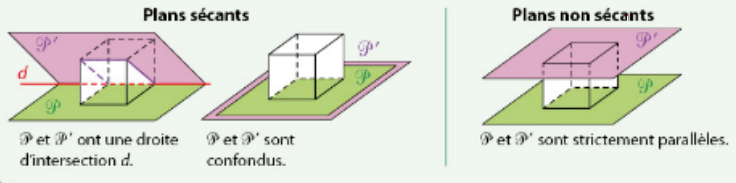
- Deux droites sont coplanaires lorsqu’elles sont contenues dans un même plan:
- Deux droites sont strictement parallèles lorsqu’elles sont coplanaires et non sécantes.
III. Droites et plans parallèles
1.Parallélisme entre droites
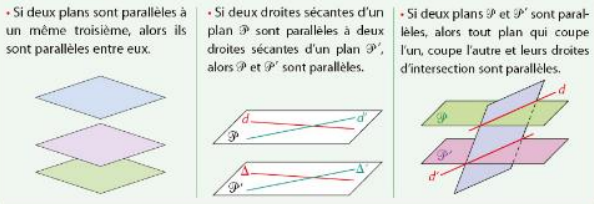
- Si deux droites sont parallèles à une même troisième, alors elles sont parallèles entre elles;
- Si deux droites sont parallèles , alors tout plan qui coupe l’une, coupe l’autre.
2.Parallélisme entre plans
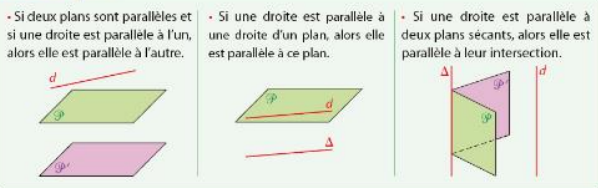
3.Parallélisme entre droites et plans
Télécharger ou imprimer cette fiche «géométrie dans l'espace : cours de maths en 2de à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Nos applications
Téléchargez la dernière version gratuite de nos applications.