La fonction affine à travers un cours de maths en 2de qui portera sur les notions d’images et d’antécédents ainsi que l’étude des courbes représentatives. L’élève devra connaître son expression algébrique qui est du type f(x)=ax+b où a est le coefficient directeur et b est l’ordonnée à l’origine. Cette leçon peut être imprimée ou téléchargée en PDF.
I. Définition de la fonction .
Définition :
Soient et deux nombres réels.
On appelle fonction affine, toute fonction f définie par .
II. Propriétés de la fonction et vocabulaire.
Propriété :
Soit f une fonction affine telle que .
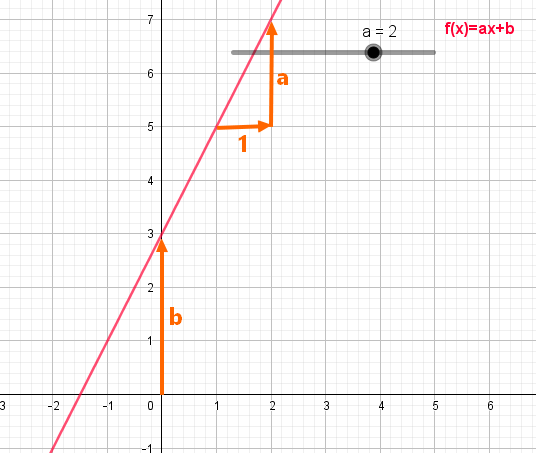
Dans un repère orthonormé du plan, la courbe d’une fonction affine est la droite d’équation y=ax + b.
Le nombre est appelé coefficient directeur de la droite.
Le nombre est appelé l’ordonnée à l’origine.
Remarque :
Une fonction linéaire est une fonction affine mais la réciproque est fausse.
Contre-exemples :
est une fonction linéaire mais aussi affine car pour tout nombre réel x, nous avons .
est une fonction affine mais n’est pas linéaire.
III. Sens de variation de la fonction.
Propriété :
Soit a et b deux nombres réels et soit f la fonction telle que f(x)=ax + b pour tout nombre réel x.
Si alors f est une fonction constante;
Si alors la fonction f est croissante;
Si alors la fonction f est décroissante.
IV. Déterminer l’expression algébrique d’une fonction affine.
Propriété :
Soit f une fonction telle que .Soient et deux points distincts appartenant à la courbe de cette fonction.
Nous avons :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «fonction affine : cours de maths en 2de à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Réviser les cours et exercices de maths avec nos Q.C.M :
et 
