Inéquations : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Exercice 1 – inéquations à résoudre.
1) Réponse : 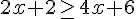
Simplifions l’inéquation :
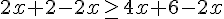
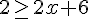
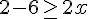
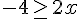
Donc,
2) Réponse : 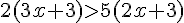
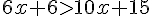
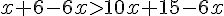
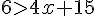
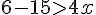
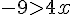
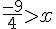
Donc, 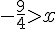
3) Réponse : 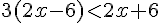
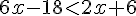
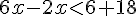
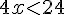
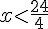
Donc, 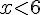
4) Réponse : 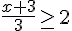
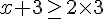
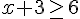
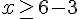
Donc, 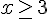
5) Réponse : 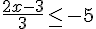
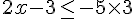
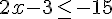
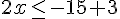
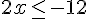
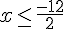
Donc, 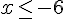
6) Réponse : 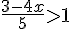
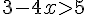
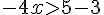
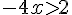
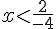
Donc, 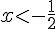
Exercice 2 – inéquation du premier degré.
1. Justifier que 0 est solution de cette inéquation :
Pour démontrer que 0 est solution, substituons 
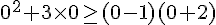
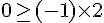
Cela donne : 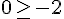
C’est vrai, donc 0 est une solution.
2. Est-ce que 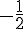
Substituons 
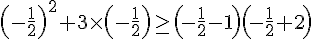
Calculons chaque côté :
Gauche : 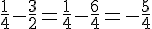
Droite : 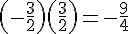
Comparaison : 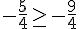
C’est vrai, donc 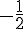
3. Résolution de l’inéquation après développement du second membre :
Développons le second membre :
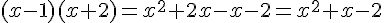
L’inéquation devient :
En simplifiant, nous obtenons :
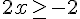
Divisons par 2 :
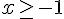
La solution de l’inéquation est donc 
Exercice 3 – résolution d’inéquations.
a.
On commence par ajouter 
Ce qui donne :
Ensuite, on ajoute 7 des deux côtés :
On divise par 3 :
Solution : 
b.
On soustrait 
On soustrait 7 des deux côtés :
On divise par 2 :
Solution : 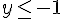
c.
On commence par développer le côté droit :
On soustrait 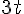
On soustrait 2 des deux côtés :
On divise par 3 :
Solution : 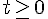
Exercice 4 – problème et inéquations.
1. Exprimer, en fonction de y, le coût à l’année avec la formule A :
Le coût total avec la formule A est donné par :
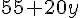
2. Exprimer, en fonction de y, le coût à l’année avec la formule B :
Le coût total avec la formule B est donné par :
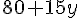
3. À partir de combien d’entrées dans l’année, la formule B se révèle-t-elle plus intéressante ?
Nous devons résoudre l’inéquation suivante :
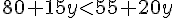
En simplifiant, cela revient à :
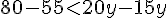
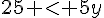
En divisant par 5 :
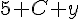
Cela signifie que la formule B devient plus intéressante à partir de 6 entrées (car y doit être un entier).
Exercice 5 – inéquation et droite graduée
Résoudre l’inéquation 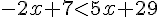
1. Soustraire 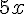
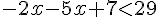
2. Simplifier :
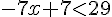
3. Soustraire 7 des deux côtés :
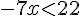
4. Diviser par 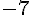
5. Représenter sur une droite graduée : la solution est l’ensemble des x tels que 
Sur la droite graduée, partez du point 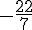

Exercice 6 – somme de 3 entiers consécutifs et inéquation.
Appelons ces trois entiers 
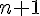
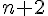
La somme de ces trois entiers est :
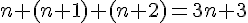
Nous avons l’inéquation suivante :
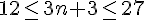
En simplifiant l’inéquation :
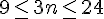
En divisant chaque membre par 3 :
Le plus grand des trois nombres est :
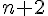
Cela implique :
Les valeurs possibles du plus grand nombre sont 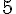
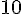
Exercice 7 – périmètre et inéquation.
Le périmètre P d’un rectangle est donné par la formule :
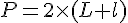
Il est donné que 

Il faut donc :
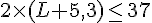
En divisant chaque membre par 2, on obtient :
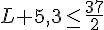
Calculons 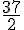
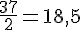
Donc :
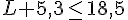
En soustrayant 5,3 de chaque côté, on trouve :
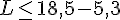
Calculons 
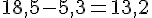
Donc, 
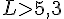
Les valeurs possibles pour la longueur L sont donc :
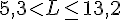
Télécharger ou imprimer cette fiche «inéquations : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.























