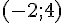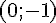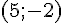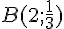Repérage dans le plan : corrigé des exercices de maths en 2de en PDF
Mis à jour le 24 novembre 2025
Exercice 1 – donner les noms des points.
Figure 1 : Le point de coordonnées 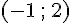
Figure 2 : Le point de coordonnées 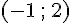
Exercice 2 – valeur de longueur et coordonnées du milieu.
1) Valeur exacte de la longueur du segment [AB] :
La formule pour calculer la longueur d’un segment selon les coordonnées de ses extrémités 

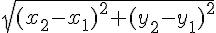
Pour les points 
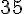
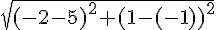
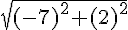
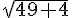
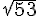
2) Coordonnées du milieu du segment [AB] :
La formule pour trouver les coordonnées du milieu est :
Pour les points 

Exercice 3 – coordonnées dans un repère et triangle.
1) Placement des points A et B :
Les points A et B ont pour coordonnées respectives A(2; -1) et B(-6; -1).
2) Construction de C tel que ABC soit isocèle en C avec hauteur 4 cm :
La médiatrice du segment AB est une droite parallèle à l’axe des ordonnées (axe y) étant donné que A et B sont alignés horizontalement. Le milieu de AB est le point M avec :
Le point 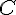

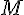

3) Coordonnées du point C :
C(-2; 3)
4) Construction du symétrique de C par rapport à (AB) :
Le symétrique de C(-2; 3) par rapport à l’axe x est le point C'(-2; -5).
5) Coordonnées de C’ :
C'(-2; -5)
Exercice 4 – construire des points dans un repère.
1) Placement des points D et E :
Les points D et E ont pour coordonnées respectives 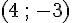
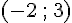
2) Construction du point F :
Pour que le triangle EDF soit équilatéral, nous devons trouver le point F de telle manière que DE = DF = EF. La longueur DE est 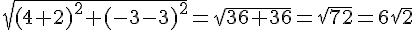
3) Coordonnées de F :
Le point F peut se situer à deux endroits possibles en utilisant la construction d’un triangle équilatéral. Les coordonnées sont 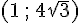
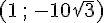
4) Symétrique de E par rapport à F :
Pour trouver le symétrique de E par rapport à F, calculons les coordonnées en prenant F comme milieu de EE’.
5) Coordonnées du symétrique :
Le symétrique de E par rapport à F est situé aux coordonnées 
Exercice 5 – coordonnées des milieux de segments.
1. Points A et B de coordonnées respectives 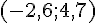
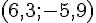
Coordonnées du milieu de [AB] :
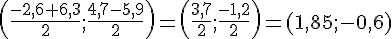
2. Points A, B et C de coordonnées respectives 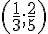
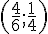
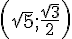
Milieu de [AB] :
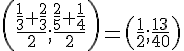
Milieu de [BC] :
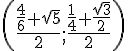
Milieu de [AC] :
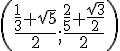
3. Points C et D de coordonnées respectives 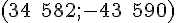
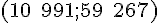
Coordonnées du point d’intersection du segment [CD] avec sa médiatrice :
La médiatrice d’un segment passe par son milieu et est perpendiculaire à ce segment. Il n’y a pas de coordonnées uniques pour ce point d’intersection autre que le milieu déjà calculé :
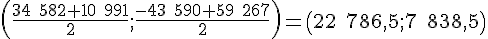
Exercice 6 – coordonnées du milieu et parallélogramme.
1) Calculer les coordonnées du point B tel que M soit le milieu de [AB].
Les coordonnées de M sont (0;3). On a A(3;-2) et M est le milieu de [AB], donc :
Coordonnées de M :
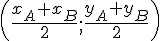
Système d’équations :
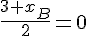
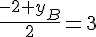
Solutions :
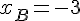
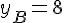
Donc, B a pour coordonnées (-3;8).
2) Calculer les coordonnées du point symétrique de E par rapport au point F.
Pour trouver les coordonnées du point symétrique E’ de E par rapport à F, on utilise la formule :
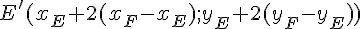
Avec E(-6;9) et F(0;-4,6), on a :
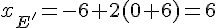
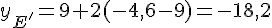
Donc, E’ a pour coordonnées (6;-18,2).
1) Calculer les coordonnées du milieu de [BN].
Coordonnées de B
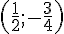
et N
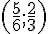
Milieu de [BN] :
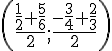
Coordonnées du milieu :
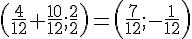
2) Calculer les coordonnées du point C tel que BANC soit un parallélogramme.
Pour que BANC soit un parallélogramme, on doit avoir
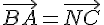
Coordonnées de A
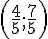
On a :
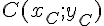
Système d’équations :
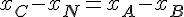
et
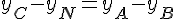
Calcul :
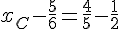
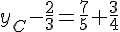
Solutions :
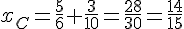
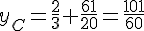
Donc, C a pour coordonnées
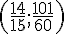
Exercice 7 – coordonnées d’un point et sommets de triangle.
Les coordonnées des sommets du triangle PAT sont:
- P :
- A :
- T :
1. Calcul des coordonnées de E :
Le point E est le milieu du segment ![[AT]](https://maths-pdf.fr/latex-images/b54b88f4efe207c7bd7cba595779e547.png)
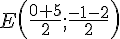
Donc E a pour coordonnées : 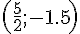
2. Calcul de la pente de la droite (TP) :
La pente de la droite 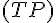
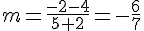
3. Équation de la parallèle à (TP) passant par E :
Cette droite a la même pente que 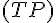
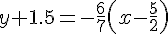
En développant :
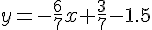
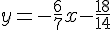
4. Intersection avec la droite (PA) :
L’équation de la droite 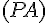
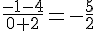
En remontant cette pente avec le point P :
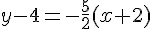
Equation simplifiée :
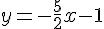
5. Résolution du système (intersection des deux droites) :
On égale les deux équations :
Afin de trouver les coordonnées de F
Les coordonnées de F sont :
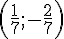
Exercice 8 – placer les symétriques et coordonnées.
1) Coordonnées des points :
Coordonnées de A : 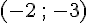
Coordonnées de B : 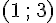
Coordonnées de C : 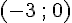
Coordonnées de D : 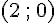
2) Symétrique E du point B par rapport à J :
Le point J a pour coordonnées 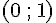
Pour trouver E, on utilise la symétrie : 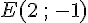
3) Coordonnées des milieux :
Milieu F de [AB] : 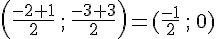
Milieu G de [AC] : 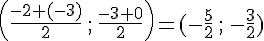
4) Calcul des distances :
Distance AC : 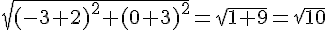
Distance CE : 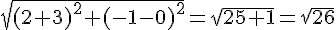
Distance AE : 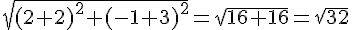
5) Nature du triangle ACE :
Le triangle ACE est rectangle car : 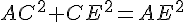
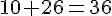
Exercice 9 – périmètre d’un triangle et coordonnées.
1) Calculer le périmètre du triangle 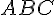
Les coordonnées des points sont :
On calcule les longueurs des côtés :
Le périmètre du triangle ABC est donc :
2) Calculer les coordonnées des points A’, B’ et C’, milieux respectifs des segments [BC], [AC] et [AB].
Coordonnées de A ‘ :
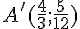
Coordonnées de B ‘ :
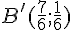
Coordonnées de C ‘ :
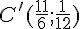
3) En déduire le périmètre du triangle A’B’C’.
On calcule les longueurs des côtés :
Le périmètre du triangle A’B’C’ est donc :
Exercice 10 – patron d’une pyramide et coordonnées.
Coordonnées des points :
A : L’origine du repère donné est au point A, donc 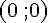
B : Comme AB est sur un côté du carré et que le côté (AD) est perpendiculaire à (AB), le point B est 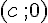
D : Le point D est sur le même côté que A et à un angle droit, donc 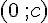
C : Le point C est où (CD) et (BC) se rejoignent, formant un carré avec D et B. Donc, 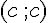
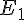
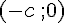
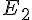
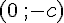
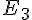
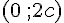
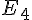
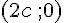
Télécharger ou imprimer cette fiche «repérage dans le plan : corrigé des exercices de maths en 2de en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.