Les suites : corrigé des exercices de maths en 1ère en PDF
Mis à jour le 25 novembre 2025
Exercice 1 – problème sur les suites récurrentes.
1) Soit 
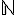

a) Exprimer 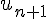

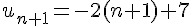
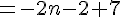
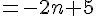
b) Exprimer 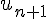

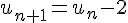
2) Soit 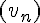


a) Exprimer 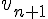

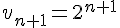
b) Exprimer 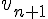
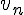
1) 



Exprimer 
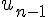
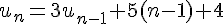
2) 
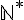


Exprimer 
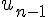
Dans ce cas, il n’y a pas de lien direct entre 
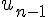
sans informations supplémentaires ou calculs intermédiaires spécifiques.
Exercice 2 – algorithme et terme d’une suite défini par sa forme explicite.
1) La suite 
La suite 
directement à l’aide d’une expression donnée dans l’algorithme : 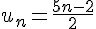
2) Définir la suite 
La suite
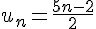
Exercice 3 – algorithme et définition d’une suite numérique.
1) Comment est définie cette suite ?
La suite 
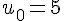
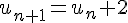
2) Que fait cet algorithme ?
L’algorithme lit un nombre 
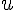
termes de la suite.
À chaque itération, il ajoute 2 au terme précédent pour obtenir le suivant.
3) Modifier cet algorithme pour qu’il n’affiche que le terme dont l’indice a été choisi par l’utilisateur.
On peut modifier l’algorithme de la manière suivante :
VARIABLES
u EST_DU_TYPE NOMBRE
n EST_DU_TYPE NOMBRE
i EST_DU_TYPE NOMBRE
DEBUT_ALGORITHME
LIRE n
u PREND_LA_VALEUR 5
POUR i ALLANT_DE 1 A n
u PREND_LA_VALEUR u+2
FIN_POUR
AFFICHER u
FIN_ALGORITHME
Cette version ne calcule que le terme 
Exercice 4 – une suite de triangles rectangles et étude de la suite de longueurs.
1) Calculer 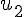
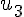
Considérons le triangle rectangle 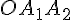
![[OA_2]](https://maths-pdf.fr/latex-images/3249472d87ed6e0c870ec0201dcafd30.png)
Comme 
Ainsi, 
Pour calculer 
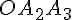
![[OA_3 ]](https://maths-pdf.fr/latex-images/5c976f6461b3bc043ac97d95075547fa.png)
Donc, 
2) Définir la suite 
Par récurrence, nous avons la relation suivante pour la suite 
3) Conjecturer la forme explicite de la suite 
En observant les valeurs calculées, nous remarquons que 
Ainsi, la conjecture pour la forme explicite est :
Exercice 5 – suite récurrente et utilisation du tableur.
Pour obtenir les premiers termes de la suite 
Dans la cellule B2 : -3
Dans la cellule C2 : =B2^2 + 3*B2
Puis, étirez la cellule C2 vers la droite pour remplir les cellules suivantes.
Exercice 6 – tableur et formule entrée dans la cellule pour une suite.
1) Quelle est la formule entrée dans la cellule C2 et recopiée vers la droite ?
La cellule C2 contient la formule pour calculer les termes de la suite 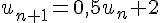
Ainsi, dans C2, la formule est =0.5*B2+2 et elle est recopiée vers la droite pour les cellules suivantes (D2, E2, etc.).
2) Quelle est la formule entrée dans la cellule C3 et recopiée vers la droite ?
La cellule C3 contient la somme partielle des termes de la suite de la ligne 2.
Ainsi, dans C3, la formule est =B3+C2 où B3 est initialisé à 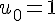
Cette formule est ensuite recopiée vers la droite pour calculer chaque somme cumulative (D3, E3, etc.).
Exercice 7 – etude de trois suites.
1) Écrire 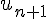
Calculons :
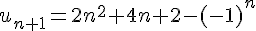
2) Écrire 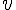

Calculons :



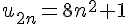
3) Écrire 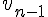

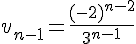
4) Écrire 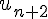

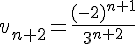
5) Calculer les 6 premiers termes de la suite 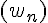

Calculons les valeurs :
6) Exprimer 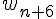
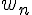
La suite (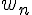
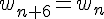
Exercice 8 – mode de génération des 4 premiers termes d’une suite.
a) La suite u est définie de manière récurrente par :
Calcul des quatre premiers termes :
– 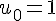
– 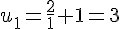
– 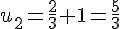
– 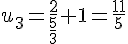
b) La suite v est définie explicitement par :
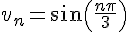
Calcul des quatre premiers termes :
– 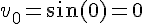
– 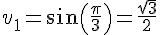
– 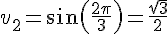
– 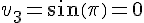
Exercice 9 – tableur et formule des termes d’une suite v.
1) En recopiant la formule écrite en C2 vers la droite, quelle valeur obtient-on dans la case D2 ?
La formule en C2 est 
Lorsque l’on copie cette formule vers la cellule D2, les références changent automatiquement vers la colonne suivante :
La formule devient 
On a donc 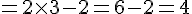
La valeur dans la case D2 est donc 4.
2) Définir la suite v.
La suite v est définie par la relation de récurrence suivante :

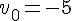
Exercice 10 – courbe des premiers termes d’une suite.
En suivant graphiquement les itérations de la suite sur le schéma, nous observons les valeurs successives des termes u_n.
En commençant avec 
Pour 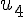
La valeur approchée de 
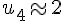
Télécharger ou imprimer cette fiche «les suites : corrigé des exercices de maths en 1ère en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
D'autres cours et exercices corrigés
Nos applications
Téléchargez la dernière version gratuite de nos applications.






















