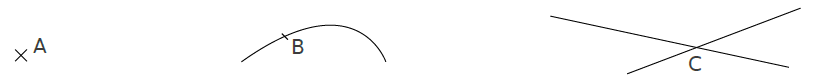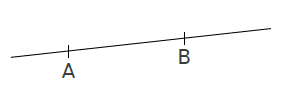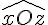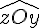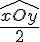Droites, segments et médiatrice : cours de maths en 6ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
Nous terminerons cette leçon avec la médiatrice d’un segment et ses propriétés d’équidistance. Cette leçon reprend toutes les notions du programme officiel de l’éducation nationale en maths et permet aux élèves de sixième d’assimiler le contenu de leur leçon. L’élève utilisera les notations des droites et segments ainsi que, les symboles de parallélisme, orthogonalité et appartenance.
I. Points et appartenance
1. Le point géométrique :
On désigne un point par une croix.
Exemples :
On dit que deux points sont confondus quand ils sont superposés.
Ils sont donc au même emplacement.
Si ce n’est pas le cas, on dit que ces points sont distincts.
Exemples :
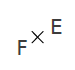
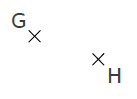
E et F sont confondus.
On note : E= F
G et H sont des points distincts, on note 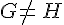
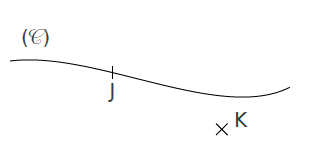
2. Appartenance à un lieu géométrique :
Exemple :
Le point 
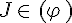

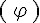
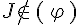
II. Droites du plan :
1. Notations :
Pour noter une droite, on utilise des parenthèses et des lettres.
La droite ci-dessus se note 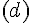
La droite ci-dessus se note 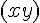
La droite ci-dessus se note 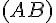
Remarques :
- une droite est infinie ;
- une droite est un ensemble infini de points ;
- par deux points distincts, il passe une et une unique droite.
2. Alignement de points du plan :
Exemple :
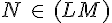
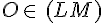
III. Demi-droite :
1.Notation d’une demi-droite :
Pour représenter une demi-droite, on utilise un crochet : [ ou ] et une parenthèse : ( ou ) .

Cette demi-droite se note 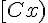
![(xC]](https://maths-pdf.fr/latex-images/d3c8cec2d47c27c24f00c5dfda33b148.png)
Le point C est son origine .
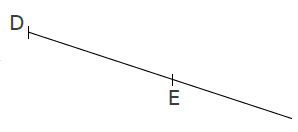
La demi-droite d’origine D passant par E se note [DE) ou (ED] .
IV. Segment
1. Notation d’un segment :
Pour noter un segment, on utilise des points : une origine et une extrémité .
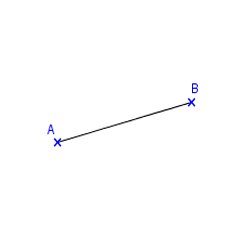
Le segment ci-dessus se note [AB] ou [BA] .
Les points A et B sont les extrémités de ce segment.
2. Longueur d’un segment :
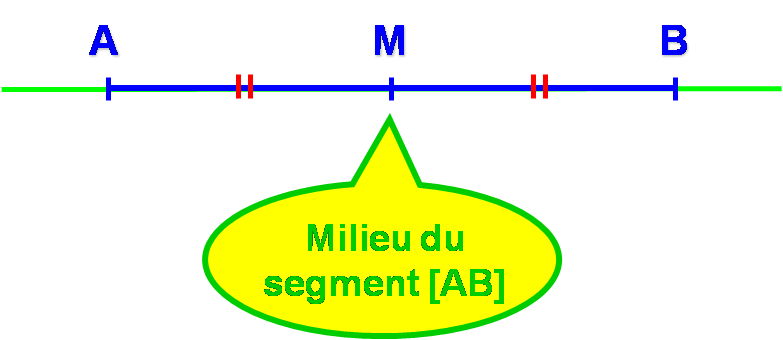
3. Milieu d’un segment :
Le milieu d’un segment est le point de ce segment qui est situé à égale distance des extrémités et qui est aligné avec les deux extrémités.
Exemple :
Je sais que : M est le milieu de [AB].
Donc je peux dire que : ![M\,\in\,[AB]](https://maths-pdf.fr/latex-images/8782dbe5688bd77cc56240098c707c59.png)
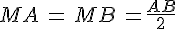
et que les points M, A et B sont alignés.
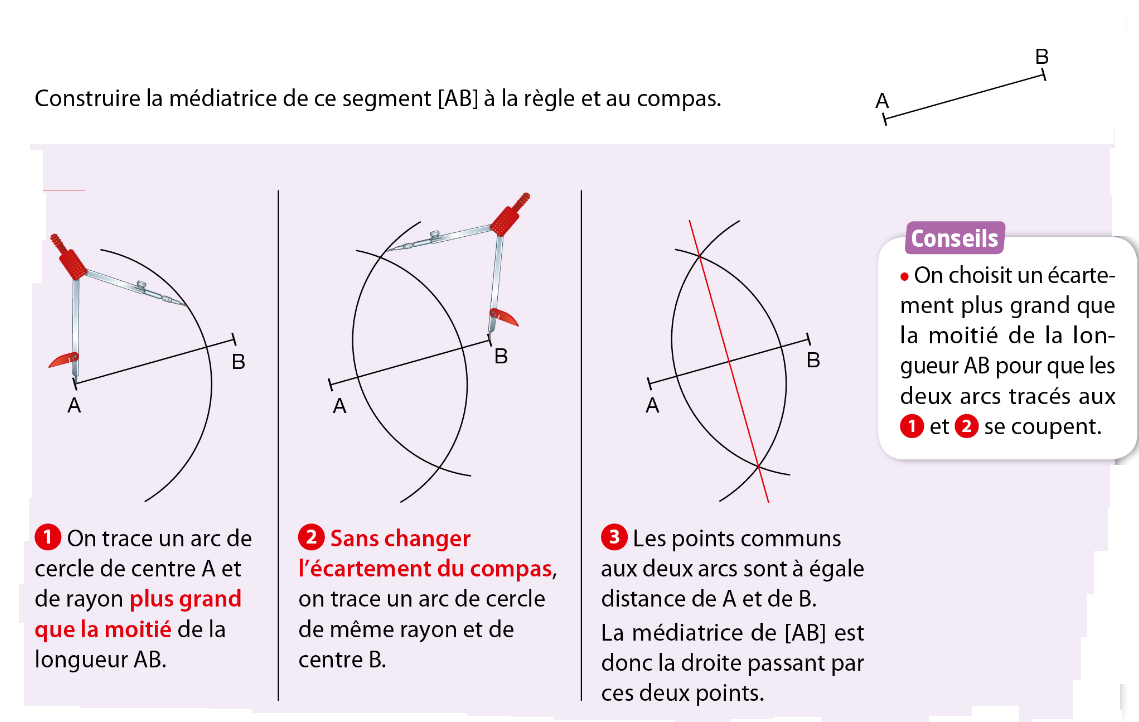
V. La médiatrice d’un segment :
La médiatrice d’un segment [AB] est la droite qui :
- passe par le milieu du segment [AB];
- est perpendiculaire au segment [AB].
Exercice :
Soit AB= 7,2 cm
Construire à la règle et au compas le milieu I du segment [AB] ainsi que sa médiatrice.
Alors M est équidistant des points A et B (c.a.d MA=MB)
Alors M appartient à la médiatrice du segment [AB]
Tout point M situé sur la médiatrice d’un segment [AB] est équidistant des sommets A et B. Nous avons donc AM=AB.
VI. Bissectrice d’un angle
1.Définition
en deux angles de même mesure .
Exemple :
[Oz) est la bissectrice de 
Remarque :
La bissectrice d’un angle est l’axe de symétrie de cet angle.
2.Construction à la règle et au rapporteur
3.Construction à la règle et au compas de la bissectrice d’un angle
Télécharger puis imprimer cette fiche en PDF.Télécharger ou imprimer cette fiche «droites, segments et médiatrice : cours de maths en 6ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 6ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.